Small, but very brave, mouse Brain was not accepted to summer school of young villains. He was upset and decided to postpone his plans of taking over the world, but to become a photographer instead.
As you may know, the coolest photos are on the film (because you can specify the hashtag #film for such).
Brain took a lot of colourful pictures on colored and black-and-white film. Then he developed and translated it into a digital form. But now, color and black-and-white photos are in one folder, and to sort them, one needs to spend more than one hour!
As soon as Brain is a photographer not programmer now, he asks you to help him determine for a single photo whether it is colored or black-and-white.
Photo can be represented as a matrix sized n × m, and each element of the matrix stores a symbol indicating corresponding pixel color. There are only 6 colors:
- 'C' (cyan)
- 'M' (magenta)
- 'Y' (yellow)
- 'W' (white)
- 'G' (grey)
- 'B' (black)
The photo is considered black-and-white if it has only white, black and grey pixels in it. If there are any of cyan, magenta or yellow pixels in the photo then it is considered colored.
The first line of the input contains two integers n and m (1 ≤ n, m ≤ 100) — the number of photo pixel matrix rows and columns respectively.
Then n lines describing matrix rows follow. Each of them contains m space-separated characters describing colors of pixels in a row. Each character in the line is one of the 'C', 'M', 'Y', 'W', 'G' or 'B'.
Print the "#Black&White" (without quotes), if the photo is black-and-white and "#Color" (without quotes), if it is colored, in the only line.
2 2
C M
Y Y
#Color
3 2
W W
W W
B B
#Black&White
1 1
W
1 /****************************** 2 code by drizzle 3 blog: www.cnblogs.com/hsd-/ 4 ^ ^ ^ ^ 5 O O 6 ******************************/ 7 #include<bits/stdc++.h> 8 #include<iostream> 9 #include<cstring> 10 #include<cstdio> 11 #include<map> 12 #include<algorithm> 13 #include<queue> 14 #define ll __int64 15 using namespace std; 16 int n,m; 17 char exm; 18 int flag=0; 19 int main() 20 { 21 scanf("%d %d",&n,&m); 22 flag=0; 23 for(int i=1; i<=n; i++) 24 { 25 getchar(); 26 scanf("%c",&exm); 27 if(exm!='W'&&exm!='B'&&exm!='G') 28 flag=1; 29 for(int j=2; j<=m; j++) 30 { 31 scanf(" %c",&exm); 32 if(exm!='W'&&exm!='B'&&exm!='G') 33 flag=1; 34 } 35 } 36 if(flag) 37 cout<<"#Color"<<endl; 38 else 39 cout<<"#Black&White"<<endl; 40 return 0; 41 }
Masha wants to open her own bakery and bake muffins in one of the n cities numbered from 1 to n. There are m bidirectional roads, each of whose connects some pair of cities.
To bake muffins in her bakery, Masha needs to establish flour supply from some storage. There are only k storages, located in different cities numbered a1, a2, ..., ak.
Unforunately the law of the country Masha lives in prohibits opening bakery in any of the cities which has storage located in it. She can open it only in one of another n - k cities, and, of course, flour delivery should be paid — for every kilometer of path between storage and bakery Masha should pay 1 ruble.
Formally, Masha will pay x roubles, if she will open the bakery in some city b (ai ≠ b for every 1 ≤ i ≤ k) and choose a storage in some city s (s = aj for some 1 ≤ j ≤ k) and b and s are connected by some path of roads of summary length x (if there are more than one path, Masha is able to choose which of them should be used).
Masha is very thrifty and rational. She is interested in a city, where she can open her bakery (and choose one of k storages and one of the paths between city with bakery and city with storage) and pay minimum possible amount of rubles for flour delivery. Please help Masha find this amount.
The first line of the input contains three integers n, m and k (1 ≤ n, m ≤ 105, 0 ≤ k ≤ n) — the number of cities in country Masha lives in, the number of roads between them and the number of flour storages respectively.
Then m lines follow. Each of them contains three integers u, v and l (1 ≤ u, v ≤ n, 1 ≤ l ≤ 109, u ≠ v) meaning that there is a road between cities u and v of length of l kilometers .
If k > 0, then the last line of the input contains k distinct integers a1, a2, ..., ak (1 ≤ ai ≤ n) — the number of cities having flour storage located in. If k = 0 then this line is not presented in the input.
Print the minimum possible amount of rubles Masha should pay for flour delivery in the only line.
If the bakery can not be opened (while satisfying conditions) in any of the n cities, print - 1 in the only line.
5 4 2
1 2 5
1 2 3
2 3 4
1 4 10
1 5
3
3 1 1
1 2 3
3
-1
Image illustrates the first sample case. Cities with storage located in and the road representing the answer are darkened.
题意：寻找最小的边权值使得烘焙屋和货源地连接
题解：最优的情况下，选择的烘培屋和货源地一定是相邻的（若不相邻则一定能找到更优的情况），否则就无解。于是枚举图的边，若当前边所连两点分别是烘焙屋和货源地的话就用边权更新最小值 ans 。枚举结束后的 ans 就是最优解。
1 /****************************** 2 code by drizzle 3 blog: www.cnblogs.com/hsd-/ 4 ^ ^ ^ ^ 5 O O 6 ******************************/ 7 #include<bits/stdc++.h> 8 #include<iostream> 9 #include<cstring> 10 #include<cstdio> 11 #include<map> 12 #include<algorithm> 13 #include<queue> 14 #define ll __int64 15 using namespace std; 16 int n,m,k; 17 struct node 18 { 19 int s,e,w; 20 }N[100005]; 21 bool cmp(struct node aa,struct node bb) 22 { 23 return aa.w<bb.w; 24 } 25 int dis[100005]; 26 int exm; 27 int main() 28 { 29 scanf("%d %d %d",&n,&m,&k); 30 memset(dis,0,sizeof(dis)); 31 for(int i=0;i<m;i++) 32 scanf("%d %d %d",&N[i].s,&N[i].e,&N[i].w); 33 for(int i=1;i<=k;i++) 34 { 35 scanf("%d",&exm); 36 dis[exm]=1; 37 } 38 sort(N,N+m,cmp); 39 for(int i=0;i<m;i++) 40 { 41 if(dis[N[i].s]!=dis[N[i].e]) 42 { 43 printf("%d ",N[i].w); 44 return 0; 45 } 46 } 47 printf("-1 "); 48 return 0; 49 }
Katya studies in a fifth grade. Recently her class studied right triangles and the Pythagorean theorem. It appeared, that there are triples of positive integers such that you can construct a right triangle with segments of lengths corresponding to triple. Such triples are called Pythagorean triples.
For example, triples (3, 4, 5), (5, 12, 13) and (6, 8, 10) are Pythagorean triples.
Here Katya wondered if she can specify the length of some side of right triangle and find any Pythagorean triple corresponding to such length? Note that the side which length is specified can be a cathetus as well as hypotenuse.
Katya had no problems with completing this task. Will you do the same?
The only line of the input contains single integer n (1 ≤ n ≤ 109) — the length of some side of a right triangle.
Print two integers m and k (1 ≤ m, k ≤ 1018), such that n, m and k form a Pythagorean triple, in the only line.
In case if there is no any Pythagorean triple containing integer n, print - 1 in the only line. If there are many answers, print any of them.
3
4 5
6
8 10
1
-1
17
144 145
67
2244 2245
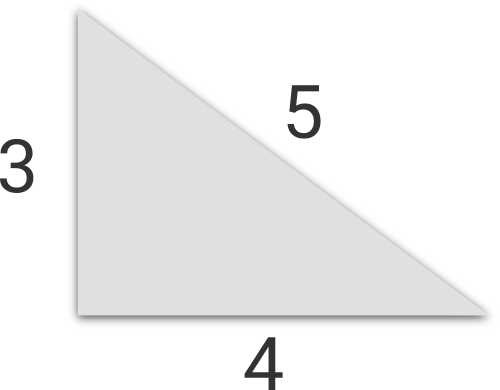
Illustration for the first sample.
题意：给你一条边 输出能够组成直角三角形的两外两条边
题解：若n为偶数 则另外两条边为n^2-1 n^2+1
若n为奇数 则另外两条边为n^2/2 n^2/2+1
特判1，2
/****************************** code by drizzle blog: www.cnblogs.com/hsd-/ ^ ^ ^ ^ O O ******************************/ #include<bits/stdc++.h> #include<iostream> #include<cstring> #include<cstdio> #include<map> #include<algorithm> #include<queue> #define ll __int64 using namespace std; ll n; int main() { scanf("%I64d",&n); if(n==1||n==2){ printf("-1 "); return 0; } if(n%2==0) { printf("%I64d %I64d ",n*n/4-1,n*n/4+1); } else { printf("%I64d %I64d ",n*n/2,n*n/2+1); } return 0; }