传递
Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 42 Accepted Submission(s): 16
Problem Description
我们称一个有向图G是传递的,当且仅当对任意三个不同的顶点a,,若G中有 一条边从a到b且有一条边从b到c ,则G中同样有一条边从a到c。
我们称图G是一个竞赛图,当且仅当它是一个有向图且它的基图是完全图。换句 话说,将完全图每条边定向将得到一个竞赛图。
下图展示的是一个有4个顶点的竞赛图。
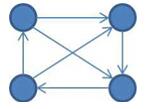
现在,给你两个有向图P = (V,Ep )和Q = (V,Ee ),满足:
1. EP 与Ee 没有公共边;
2. (V,Ep⋃Ee )是一个竞赛图。
你的任务是:判定是否P,Q同时为传递的。
我们称图G是一个竞赛图,当且仅当它是一个有向图且它的基图是完全图。换句 话说,将完全图每条边定向将得到一个竞赛图。
下图展示的是一个有4个顶点的竞赛图。

现在,给你两个有向图P = (V,Ep )和Q = (V,Ee ),满足:
1. EP 与Ee 没有公共边;
2. (V,Ep⋃Ee )是一个竞赛图。
你的任务是:判定是否P,Q同时为传递的。
Input
包含至多20组测试数据。
第一行有一个正整数,表示数据的组数。
对于每组数据,第一行有一个正整数n。接下来n行,每行为连续的n个字符,每 个字符只可能是’-’,’P’,’Q’中的一种。
∙ 如果第i行的第j个字符为’P’,表示有向图P中有一条边从i到j;
∙ 如果第i行的第j个字符为’Q’,表示有向图Q中有一条边从i到j;
∙ 否则表示两个图中均没有边从i到j。
保证1 <= n <= 2016,一个测试点中的多组数据中的n的和不超过16000。保证输入的图一定满足给出的限制条件。
第一行有一个正整数,表示数据的组数。
对于每组数据,第一行有一个正整数n。接下来n行,每行为连续的n个字符,每 个字符只可能是’-’,’P’,’Q’中的一种。
∙ 如果第i行的第j个字符为’P’,表示有向图P中有一条边从i到j;
∙ 如果第i行的第j个字符为’Q’,表示有向图Q中有一条边从i到j;
∙ 否则表示两个图中均没有边从i到j。
保证1 <= n <= 2016,一个测试点中的多组数据中的n的和不超过16000。保证输入的图一定满足给出的限制条件。
Output
对每个数据,你需要输出一行。如果P! Q都是传递的,那么请输出’T’。否则, 请输出’N’ (均不包括引号)。
Sample Input
4
4
-PPP
--PQ
---Q
----
4
-P-P
--PQ
P--Q
----
4
-PPP
--QQ
----
--Q-
4
-PPP
--PQ
----
--Q-
Sample Output
T
N
T
N
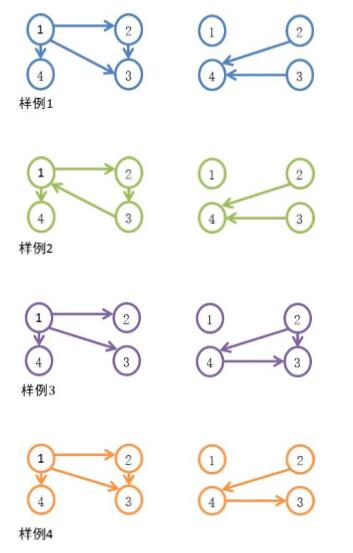
Hint
在下面的示意图中,左图为图为Q。
Source
题意:中文题面
题解:a->b->c 枚举中间点b 判断中间点的先驱点集a 的后继点集合是否含于c
bitset 处理;
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<vector> 5 #include<bitset> 6 #define ll __int64 7 using namespace std; 8 int t; 9 char mp[2500][2500]; 10 vector<int> p[2500]; 11 vector<int> q[2500]; 12 struct node 13 { 14 bitset<2500> from; 15 bitset<2500> to; 16 } pp[2500],qq[2500]; 17 int n; 18 void init() 19 { 20 for(int i=0; i<n; i++) 21 { 22 p[i].clear(); 23 q[i].clear(); 24 pp[i].from.reset(); 25 pp[i].to.reset(); 26 qq[i].from.reset(); 27 qq[i].to.reset(); 28 } 29 } 30 int main() 31 { 32 scanf("%d",&t); 33 for(int i=1; i<=t; i++) 34 { 35 scanf("%d",&n); 36 init(); 37 for(int j=0; j<n; j++) 38 scanf("%s",mp[j]); 39 for(int j=0; j<n; j++) 40 { 41 for(int k=0; k<n; k++) 42 { 43 if(mp[j][k]=='P') 44 p[j].push_back(k); 45 if(mp[j][k]=='Q') 46 q[j].push_back(k); 47 } 48 } 49 int flag1=1,flag2=1; 50 for(int k=0; k<n; k++) 51 { 52 for(int j=0;j<p[k].size();j++) 53 { 54 pp[k].to[p[k][j]]=1; 55 pp[p[k][j]].from[k]=1; 56 } 57 for(int j=0;j<q[k].size();j++) 58 { 59 qq[k].to[q[k][j]]=1; 60 qq[q[k][j]].from[k]=1; 61 } 62 } 63 for(int k=0; k<n; k++) 64 { 65 for(int l=0; l<n; l++) 66 { 67 if(pp[k].from[l]==1) 68 { 69 bitset<2500> exm; 70 exm=pp[l].to&pp[k].to; 71 if(exm!=pp[k].to) 72 { 73 flag1=0; 74 break; 75 } 76 } 77 } 78 for(int l=0; l<n; l++) 79 { 80 if(qq[k].from[l]==1) 81 { 82 bitset<2500> exm; 83 exm=qq[l].to&qq[k].to; 84 if(exm!=qq[k].to) 85 { 86 flag2=0; 87 break; 88 } 89 } 90 } 91 } 92 if(flag1&&flag2) 93 cout<<"T"<<endl; 94 else 95 cout<<"N"<<endl; 96 } 97 return 0; 98 }