We all know that GukiZ often plays with arrays.
Now he is thinking about this problem: how many arrays a, of length n, with non-negative elements strictly less then 2l meet the following condition: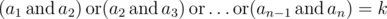 
? Here operation 
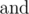means bitwise AND (in Pascal it is equivalent to and, in C/C++/Java/Python it is equivalent to &), operation 
means bitwise OR (in Pascal it is equivalent to , in C/C++/Java/Python it is equivalent to |).
Because the answer can be quite large, calculate it modulo m. This time GukiZ hasn't come up with solution, and needs you to help him!
First and the only line of input contains four integers n, k, l, m (2 ≤ n ≤ 1018, 0 ≤ k ≤ 1018, 0 ≤ l ≤ 64, 1 ≤ m ≤ 109 + 7).
In the single line print the number of arrays satisfying the condition above modulo m.
2 1 2 10
3
2 1 1 3
1
3 3 2 10
9
In the first sample, satisfying arrays are {1, 1}, {3, 1}, {1, 3}.
In the second sample, only satisfying array is {1, 1}.
In the third sample, satisfying arrays are {0, 3, 3}, {1, 3, 2}, {1, 3, 3}, {2, 3, 1}, {2, 3, 3}, {3, 3, 0}, {3, 3, 1}, {3, 3, 2}, {3, 3, 3}.
题意：n个小于(2^l)的数执行要求的运算等于K的方案数%m的结果
题解：from jhz033
思路：首先看到或，并就想将这个数拆开为二进制的01串，分别考虑每一位的0，1；
当前k的那个位置为0时，表示a1-an中没有两个相邻的1；
同理，当前k为为1时，表示a1-an中有两个相邻的1；2^n,减去0的方案即是；
刚刚开始一直在想组合数学的求法，发现不好写（。。。我也不会）
后来发现dp可以做，但是n很大；
dp方程：dp[i][0]=dp[i-1][1]+dp[i-1][0];
dp[i][1]=dp[i-1][0];
dp[i][j]表示第i位为j的无相邻1的方案数；
乍一看很像斐波那契，构造矩阵；
[ 1 , 1 ]
[ dp[i-1][0] , dp[i-1][1] ] *[ 1 , 0 ] =[ dp[i][0] , dp[i][1] ];
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 using namespace std; 14 ll n,k,l,m; 15 struct matrix 16 { 17 ll m[5][5]; 18 } ans,exm; 19 20 struct matrix matrix_mulit(struct matrix aa,struct matrix bb) 21 { 22 struct matrix there; 23 for(int i=0;i<2;i++) 24 { 25 for(int j=0;j<2;j++) 26 { 27 there.m[i][j]=0; 28 for(int k=0;k<2;k++) 29 there.m[i][j]=(there.m[i][j]+aa.m[i][k]*bb.m[k][j]%m)%m; 30 } 31 } 32 return there; 33 } 34 ll matrix_quick(ll gg) 35 { 36 exm.m[0][0]=exm.m[0][1]=exm.m[1][0]=1; 37 exm.m[1][1]=0; 38 ans.m[0][0]=1;ans.m[1][1]=0; 39 ans.m[0][1]=1;ans.m[1][0]=0; 40 if(gg==0) 41 return 1; 42 while(gg) 43 { 44 if(gg&1) 45 { 46 ans=matrix_mulit(ans,exm); 47 } 48 exm = matrix_mulit(exm, exm); 49 gg >>= 1; 50 } 51 return (ans.m[0][0]+ans.m[0][1])%m; 52 } 53 ll quick(ll aa,ll bb) 54 { 55 ll re=1; 56 while(bb) 57 { 58 if(bb&1) 59 { 60 re=(re*aa)%m; 61 } 62 aa=(aa*aa)%m; 63 bb>>=1; 64 } 65 return re; 66 } 67 int main() 68 { 69 scanf("%I64d %I64d %I64d %I64d",&n,&k,&l,&m); 70 ll ling=0,yi=0; 71 int flag=0; 72 while(k) 73 { 74 if(k%2==0) 75 ling++; 76 else 77 yi++; 78 if(ling+yi>l&&k%2==1) 79 { 80 flag=1; 81 } 82 k>>=1; 83 } 84 if(flag) 85 { 86 printf("0 "); 87 return 0; 88 } 89 ll lingmod=0,yimod=0; 90 lingmod=matrix_quick(n-1); 91 yimod=((quick(2,n)-lingmod)%m+m)%m; 92 ling+=l-(yi+ling); 93 printf("%I64d ",quick(lingmod,ling)*quick(yimod,yi)%m); 94 return 0; 95 }