Codeforces Round #336 (Div. 2)B 暴力 C dp D 区间dp

B. Hamming Distance Sum

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Genos needs your help. He was asked to solve the following programming problem by Saitama:

The length of some string s is denoted |s|. The Hamming distance between two strings s and t of equal length is defined as 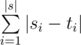, where s_i is the i-th character of s and t_i is the i-th character of t. For example, the Hamming distance between string "0011" and string "0110" is |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2.

Given two binary strings a and b, find the sum of the Hamming distances between a and all contiguous substrings of b of length |a|.

Input

The first line of the input contains binary string a (1 ≤ |a| ≤ 200 000).

The second line of the input contains binary string b (|a| ≤ |b| ≤ 200 000).

Both strings are guaranteed to consist of characters '0' and '1' only.

Output

Print a single integer — the sum of Hamming distances between a and all contiguous substrings of b of length |a|.

Examples

Input

01
00111

Output

3

Input

0011
0110

Output

2

Note

For the first sample case, there are four contiguous substrings of b of length |a|: "00", "01", "11", and "11". The distance between "01" and "00" is |0 - 0| + |1 - 0| = 1. The distance between "01" and "01" is |0 - 0| + |1 - 1| = 0. The distance between "01" and "11" is |0 - 1| + |1 - 1| = 1. Last distance counts twice, as there are two occurrences of string "11". The sum of these edit distances is 1 + 0 + 1 + 1 = 3.

The second sample case is described in the statement.

题意：给你两个01串s，t ; 在t中取连续的长度为|s|的部分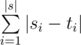 求和输出

题解：对于s串中的每一个位置i的数都与t串中[i,lent-(lens-i)]计算一次，记录t串中的1的前缀乱搞。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<vector>
#include<bitset>
#include<set>
#define ll __int64
#define mod 100000000
using namespace std;
char a[200005];
char b[200005];
int sum1[200005];
int sum0[200005];
int main()
{
    scanf("%s",a+1);
    scanf("%s",b+1);
    int len1=strlen(b+1);
    int len2=strlen(a+1);
    sum0[0]=0;
    sum1[0]=0;
   for(int i=1;i<=len1;i++)
   {
       sum1[i]=sum1[i-1];
       sum0[i]=sum0[i-1];
       if(b[i]=='1')
        sum1[i]++;
        else
        sum0[i]++;
   }
   ll ans=0;
    for(int i=1;i<=len2;i++){
        if(a[i]=='0')
           ans=ans+sum1[len1-(len2-i)]-sum1[i-1];
        else
        ans=ans+sum0[len1-(len2-i)]-sum0[i-1];
    }
    printf("%I64d
",ans);
    return 0;
}

C. Chain Reaction

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are n beacons located at distinct positions on a number line. The i-th beacon has position a_i and power level b_i. When the i-th beacon is activated, it destroys all beacons to its left (direction of decreasing coordinates) within distance b_i inclusive. The beacon itself is not destroyed however. Saitama will activate the beacons one at a time from right to left. If a beacon is destroyed, it cannot be activated.

Saitama wants Genos to add a beacon strictly to the right of all the existing beacons, with any position and any power level, such that the least possible number of beacons are destroyed. Note that Genos's placement of the beacon means it will be the first beacon activated. Help Genos by finding the minimum number of beacons that could be destroyed.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 100 000) — the initial number of beacons.

The i-th of next n lines contains two integers a_i and b_i (0 ≤ a_i ≤ 1 000 000, 1 ≤ b_i ≤ 1 000 000) — the position and power level of the i-th beacon respectively. No two beacons will have the same position, so a_i ≠ a_j if i ≠ j.

Output

Print a single integer — the minimum number of beacons that could be destroyed if exactly one beacon is added.

Examples

Input

4
1 9
3 1
6 1
7 4

Output

1

Input

7
1 1
2 1
3 1
4 1
5 1
6 1
7 1

Output

3

Note

For the first sample case, the minimum number of beacons destroyed is 1. One way to achieve this is to place a beacon at position 9 with power level 2.

For the second sample case, the minimum number of beacons destroyed is 3. One way to achieve this is to place a beacon at position 1337 with power level 42.

题意：给你n个灯塔的位置与高度 现在 在最右边增加一个灯塔  输出最少能覆盖的灯塔的个数

题解：dp[i]  表示以第i个灯塔为（最右边一个没有被覆盖的灯塔）的左边的灯塔覆盖个数

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<vector>
#include<bitset>
#include<set>
#define ll __int64
#define mod 100000000
using namespace std;
int n;
int mp[1000006];
int dp[1000006];
int sum[1000006];
int a,b;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d %d",&a,&b);
        mp[a]=b;
        }
    if(mp[0]==0){
        sum[0]=0;
        dp[0]=0;
    }
    else
    {
        sum[0]=1;
        dp[0]=0;
    }
    int ans=1e9;;
    for(int i=1;i<=1000001;i++){
        sum[i]=sum[i-1];
        if(mp[i]!=0)
          sum[i]++;
        }
    for(int i=1;i<=1000000;i++)
    {
       if(mp[i]==0)
           dp[i]=dp[i-1];
       else
       {
           int now=max(0,i-mp[i]);
           if(now==0)
           dp[i]=sum[i-1];
           else
           dp[i]=dp[now-1]+(sum[i-1]-sum[now-1]);
       }
       ans=min(ans,dp[i]+sum[1000000]-sum[i]);
    }
     printf("%d
",ans);
    return 0;
}

D. Zuma

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Genos recently installed the game Zuma on his phone. In Zuma there exists a line of n gemstones, the i-th of which has color c_i. The goal of the game is to destroy all the gemstones in the line as quickly as possible.

In one second, Genos is able to choose exactly one continuous substring of colored gemstones that is a palindrome and remove it from the line. After the substring is removed, the remaining gemstones shift to form a solid line again. What is the minimum number of seconds needed to destroy the entire line?

Let us remind, that the string (or substring) is called palindrome, if it reads same backwards or forward. In our case this means the color of the first gemstone is equal to the color of the last one, the color of the second gemstone is equal to the color of the next to last and so on.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 500) — the number of gemstones.

The second line contains n space-separated integers, the i-th of which is c_i (1 ≤ c_i ≤ n) — the color of the i-th gemstone in a line.

Output

Print a single integer — the minimum number of seconds needed to destroy the entire line.

Examples

Input

3
1 2 1

Output

1

Input

3
1 2 3

Output

3

Input

7
1 4 4 2 3 2 1

Output

2

Note

In the first sample, Genos can destroy the entire line in one second.

In the second sample, Genos can only destroy one gemstone at a time, so destroying three gemstones takes three seconds.

In the third sample, to achieve the optimal time of two seconds, destroy palindrome 4 4 first and then destroy palindrome 1 2 3 2 1.

 题意：消除回文 问最少几次消除全部

 题解：简单区间dp

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<vector>
#include<bitset>
#include<set>
#define ll __int64
#define mod 100000000
using namespace std;
int n;
int a[505];
int dp[505][505];
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
        for(int j=i;j<=n;j++)
        dp[i][j]=1e9;
    for(int i=1;i<=n;i++)
        dp[i][i]=1;
    for(int i=n;i>=1;i--)
    {
        for(int j=i+1;j<=n;j++)
        {
            for(int k=i;k<=j;k++)
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
             if(a[i]==a[j]){
                if(i+1==j)
                    dp[i][j]=1;
                else
                dp[i][j]=min(dp[i][j],dp[i+1][j-1]);
                }
        }
    }
    printf("%d
",dp[1][n]);
    return 0;
}