欢迎转载,转载请注明出处,徽沪一郎。
概要
本文就拟牛顿法L-BFGS的由来做一个简要的回顾,然后就其在spark mllib中的实现进行源码走读。
拟牛顿法
数学原理









代码实现
L-BFGS算法中使用到的正则化方法是SquaredL2Updater。
算法实现上使用到了由scalanlp的成员项目breeze库中的BreezeLBFGS函数,mllib中自定义了BreezeLBFGS所需要的DiffFunctions.
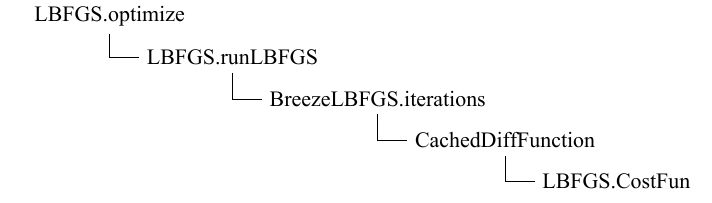
runLBFGS函数的源码实现如下
def runLBFGS(
data: RDD[(Double, Vector)],
gradient: Gradient,
updater: Updater,
numCorrections: Int,
convergenceTol: Double,
maxNumIterations: Int,
regParam: Double,
initialWeights: Vector): (Vector, Array[Double]) = {
val lossHistory = new ArrayBuffer[Double](maxNumIterations)
val numExamples = data.count()
val costFun =
new CostFun(data, gradient, updater, regParam, numExamples)
val lbfgs = new BreezeLBFGS[BDV[Double]](maxNumIterations, numCorrections, convergenceTol)
val states =
lbfgs.iterations(new CachedDiffFunction(costFun), initialWeights.toBreeze.toDenseVector)
/**
* NOTE: lossSum and loss is computed using the weights from the previous iteration
* and regVal is the regularization value computed in the previous iteration as well.
*/
var state = states.next()
while(states.hasNext) {
lossHistory.append(state.value)
state = states.next()
}
lossHistory.append(state.value)
val weights = Vectors.fromBreeze(state.x)
logInfo("LBFGS.runLBFGS finished. Last 10 losses %s".format(
lossHistory.takeRight(10).mkString(", ")))
(weights, lossHistory.toArray)
}
costFun函数是算法实现中的重点
private class CostFun(
data: RDD[(Double, Vector)],
gradient: Gradient,
updater: Updater,
regParam: Double,
numExamples: Long) extends DiffFunction[BDV[Double]] {
private var i = 0
override def calculate(weights: BDV[Double]) = {
// Have a local copy to avoid the serialization of CostFun object which is not serializable.
val localData = data
val localGradient = gradient
val (gradientSum, lossSum) = localData.aggregate((BDV.zeros[Double](weights.size), 0.0))(
seqOp = (c, v) => (c, v) match { case ((grad, loss), (label, features)) =>
val l = localGradient.compute(
features, label, Vectors.fromBreeze(weights), Vectors.fromBreeze(grad))
(grad, loss + l)
},
combOp = (c1, c2) => (c1, c2) match { case ((grad1, loss1), (grad2, loss2)) =>
(grad1 += grad2, loss1 + loss2)
})
/**
* regVal is sum of weight squares if it's L2 updater;
* for other updater, the same logic is followed.
*/
val regVal = updater.compute(
Vectors.fromBreeze(weights),
Vectors.dense(new Array[Double](weights.size)), 0, 1, regParam)._2
val loss = lossSum / numExamples + regVal
/**
* It will return the gradient part of regularization using updater.
*
* Given the input parameters, the updater basically does the following,
*
* w' = w - thisIterStepSize * (gradient + regGradient(w))
* Note that regGradient is function of w
*
* If we set gradient = 0, thisIterStepSize = 1, then
*
* regGradient(w) = w - w'
*
* TODO: We need to clean it up by separating the logic of regularization out
* from updater to regularizer.
*/
// The following gradientTotal is actually the regularization part of gradient.
// Will add the gradientSum computed from the data with weights in the next step.
val gradientTotal = weights - updater.compute(
Vectors.fromBreeze(weights),
Vectors.dense(new Array[Double](weights.size)), 1, 1, regParam)._1.toBreeze
// gradientTotal = gradientSum / numExamples + gradientTotal
axpy(1.0 / numExamples, gradientSum, gradientTotal)
i += 1
(loss, gradientTotal)
}
}
}