基于客户数据的银行信用卡风险控制模型研究-金融风控模型标准评分卡

转自基于客户数据的银行信用卡风险控制模型研究,金融,风控,建模,实战,,评分,A (pythonf.cn)

 

基于客户数据的银行信用卡风险控制模型研究,金融,风控,建模,实战,以,某,制作,评分,A

一、知识准备

1.1 熟悉Python的数据分析库numpy、pandas和scikit算法库

1. 2 熟悉逻辑回归和随机森林算法

二、项目主题

在银行借贷场景中，评分卡是一种以分数形式来衡量一个客户的信用风险大小的手段，它衡量向别人借钱的人（受信人，需要融资的公司）不能如期履行合同中的还本付息责任，并让借钱给别人的人（授信人，银行等金融机构）， 造成经济损失的可能性。一般来说，评分卡打出的分数越高，客户的信用越好，风险越小。

这些”借钱的人“，可能是个人，有可能是有需求的公司和企业。对于企业来说，我们按照融资主体的融资用途，分
别使用企业融资模型，现金流融资模型，项目融资模型等模型。而对于个人来说，我们有”四张卡“来评判个人的信用程度：A卡，B卡，C卡和F卡。而众人常说的“评分卡”其实是指A卡，又称为申请者评级模型，主要应用于相关融资类业务中新用户的主体评级，即判断金融机构是否应该借钱给一个新用户，如果这个人的风险太高，我们可以拒 绝贷款。

三、项目目标

• 能够使用RF算法对缺失值进行补充

• 能够掌握样本不平衡问题

• 熟练掌握评分卡的分箱操作

四、知识要点

4.1 原始数据

4.1.1 导库/获取数据

%matplotlib inline 
import numpy as np 
import pandas as pd 

data = pd.read_csv("Acard.csv",index_col=0)
#观察数据类型 
data.head() 

#观察数据结构 
data.shape

data.info() # 每列的缺失值情况

 

4.1.2 去重复值

data.drop_duplicates(inplace=True) 

data.index = range(data.shape[0]) 
  
data.info()

 

4.1.3 填补缺失值

data.isnull().sum()/data.shape[0]  # data.isnull().mean() 

data["NumberOfDependents"].fillna(int(data["NumberOfDependents"].mean()),inplace=True) 
  
data.isnull().mean() 

def fill_missing_rf(X, y, to_fill):
    """
    X：要填补的特征矩阵
    y：完整的，没有缺失值的标签
    to_fill：字符串，要填补的那一列的名称/MonthlyIncome
    """
    # 构建新特征矩阵和新标签
    df = X.copy() 
    fill = df.loc[:, to_fill]
    df = pd.concat([df.loc[:, df.columns != to_fill], pd.DataFrame(y)], axis=1)

    #找出训练集和测试集
    Ytrain = fill[fill.notnull()]
    Ytest = fill[fill.isnull()]
    Xtrain = df.iloc[Ytrain.index, :]
    Xtest = df.iloc[Ytest.index, :]

    from sklearn.ensemble import RandomForestRegressor as rfr
    
    #用随机森林回归来填补缺失值
    rfr = rfr(n_estimators=100)
    rfr = rfr.fit(Xtrain, Ytrain)
    Ypredict = rfr.predict(Xtest)
    
    return Ypredict

X = data.iloc[:,1:] 
y = data["SeriousDlqin2yrs"] 

y_pred = fill_missing_rf(X,y,"MonthlyIncome") 
  
#确认我们的结果合理之后，我们就可以将数据覆盖了 
data.loc[data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"] = y_pred

y_pred.shape

 

4.2 描述性统计

4.2.1 处理异常值

import seaborn as sns
from matplotlib import pyplot as plt

x1=data['age']
fig,axes = plt.subplots()
axes.boxplot(x1)
axes.set_xticklabels(['age'])

data = data[data['age']>0]
data = data[data['age']<100]

 

data.describe([0.01,0.1,0.25,.5,.75,.9,.99])
(data["age"] == 0).sum() 

data = data[data["age"] != 0] 

data[data.loc[:,"NumberOfTimes90DaysLate"] > 90].count() 
  
data = data[data.loc[:,"NumberOfTimes90DaysLate"] < 90] 

data.index = range(data.shape[0]) 
data.info() 

 

4.2.2 处理样本不均衡问题

#探索标签的分布 
X = data.iloc[:,1:] 
y = data.iloc[:,0] 
y.value_counts() 
  
n_sample = X.shape[0] 
  
n_1_sample = y.value_counts()[1] 
n_0_sample = y.value_counts()[0] 

grouped = data['SeriousDlqin2yrs'].groupby(data['SeriousDlqin2yrs']).count()
grouped.plot(kind='bar')


print('样本个数：{}; 1占{:.2%}; 0占 {:.2%}'.format(n_sample,n_1_sample/n_sample,n_0_sample/n_sample)) 

 

样本个数：149152; 1占6.62%; 0占 93.38%

from imblearn.over_sampling import SMOTE  #conda install -c glemaitre imbalanced-learn
import imblearn 
  
from imblearn.over_sampling import SMOTE 
  
sm = SMOTE(random_state=42) #实例化 
X,y = sm.fit_sample(X,y) 

n_sample_ = X.shape[0] 
  
pd.Series(y).value_counts() 
  
n_1_sample = pd.Series(y).value_counts()[1] 
n_0_sample = pd.Series(y).value_counts()[0] 
  
print('样本个数：{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample_,n_1_sample/n_sample_,n_0_sample/n_sample_))
  

 

样本个数：278560; 1占50.00%; 0占50.00%

4.2.3 训练集和测试集

from sklearn.model_selection import train_test_split 

X = pd.DataFrame(X) 
y = pd.DataFrame(y) 
  
X_train, X_vali, Y_train, Y_vali = train_test_split(X,y,test_size=0.3,random_state=420)
model_data = pd.concat([Y_train, X_train], axis=1) 
model_data.index = range(model_data.shape[0]) 
model_data.columns = data.columns 
  
vali_data = pd.concat([Y_vali, X_vali], axis=1) 
vali_data.index = range(vali_data.shape[0]) 
vali_data.columns = data.columns 
  
model_data.to_csv("model_data.csv") 
  
vali_data.to_csv("vali_data.csv") 

 

4.3 分箱处理

4.3.1 等频分箱

#retbins 默认为False，为True是返回值是元组
#q：分组个数
  
model_data["qcut"], updown = pd.qcut(model_data["age"], retbins=True, q=20) 

coount_y0 = model_data[model_data["SeriousDlqin2yrs"] == 0].groupby(by="qcut").count() ["SeriousDlqin2yrs"] 
coount_y1 = model_data[model_data["SeriousDlqin2yrs"] == 1].groupby(by="qcut").count() ["SeriousDlqin2yrs"] 
  
#num_bins值分别为每个区间的上界，下界，0出现的次数，1出现的次数 
num_bins = [*zip(updown,updown[1:],coount_y0,coount_y1)] 
  
#注意zip会按照最短列来进行结合 
num_bins

 

4.3.2 封装WOE和IV函数

• 为了衡量特征上的信息量以及特征对预测函数的贡献，银行业定义了概念Information value(IV)

• IV = (good% - bad%) * WOE

• 银行业中用来衡量违约概率的指标，中文叫做证据权重(weight of Evidence)，本质其实就是优质客户 比上坏客户的比例的对数。WOE是对一个箱子来说的，WOE越大，代表了这个箱子里的优质客户越多。

• WOE = ln(good% / bad%)

def get_woe(num_bins):
    columns = ["min","max","count_0","count_1"]  
    df = pd.DataFrame(num_bins,columns=columns)
    df["total"] = df.count_0 + df.count_1 
    df["percentage"] = df.total / df.total.sum() 
    df["bad_rate"] = df.count_1 / df.total 
    df["good%"] = df.count_0/df.count_0.sum() 
    df["bad%"] = df.count_1/df.count_1.sum() 
    df["woe"] = np.log(df["good%"] / df["bad%"])
    return df


# 计算IV值 
def get_iv(df):
    rate = df["good%"] - df["bad%"]
    iv = np.sum(rate * df.woe)
    return iv 

 

4.3.3 用卡方检验来合并箱体画出IV曲线

num_bins_ = num_bins.copy()

import matplotlib.pyplot as plt
import scipy

IV = []
axisx = []

while len(num_bins_) > 2:
    pvs = []
    
    for i in range(len(num_bins_) - 1):
        x1 = num_bins_[i][2:]
        x2 = num_bins_[i + 1][2:]
        
        pv = scipy.stats.chi2_contingency([x1, x2])[1]
        pvs.append(pv)

    
    i = pvs.index(max(pvs))
    num_bins_[i:i + 2] = [(num_bins_[i][0],num_bins_[i+1][1],num_bins_[i][2]+num_bins_[i+1][2],num_bins_[i][3]+num_bins_[i+1][3])]

    bins_df = get_woe(num_bins_)
    axisx.append(len(num_bins_))
    IV.append(get_iv(bins_df))

plt.figure()
plt.plot(axisx, IV)
plt.xticks(axisx)
plt.xlabel("number of box") 
plt.ylabel("IV") 
plt.show() 

 

def get_bin(num_bins_,n):
    while len(num_bins_) > n:
        pvs = []
        # 获取 num_bins_两两之间的卡方检验的置信度（或卡方值）
        for i in range(len(num_bins_) - 1):
            x1 = num_bins_[i][2:]
            x2 = num_bins_[i + 1][2:]
            # 0 返回 chi2 值，1 返回 p 值。 
            pv = scipy.stats.chi2_contingency([x1, x2])[1]
            # chi2 = scipy.stats.chi2_contingency([x1,x2])[0]       
            pvs.append(pv)

        # 通过 p 值进行处理。合并 p 值最大的两组
        i = pvs.index(max(pvs))
        num_bins_[i:i + 2] = [(num_bins_[i][0],num_bins_[i+1][1],num_bins_[i][2]+num_bins_[i+1][2],num_bins_[i][3]+num_bins_[i+1][3])]
        
    return num_bins_

 

4.3.4 用最佳分箱个数分箱，并验证分箱结果

def graphforbestbin(DF, X, Y, n=5,q=20,graph=True):
    DF = DF[[X,Y]].copy()
    DF["qcut"],bins = pd.qcut(DF[X],retbins=True,q=q,duplicates="drop")
    coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut").count()[Y]
    coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut").count()[Y]
    num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)]
    # 确保每个箱中都有0和1
    for i in range(q):
        if 0 in num_bins[0][2:]:
            num_bins[0:2] = [(num_bins[0][0],num_bins[1][1],num_bins[0][2]+num_bins[1][2],num_bins[0][3]+num_bins[1][3])]
            continue
        for i in range(len(num_bins)):
            if 0 in num_bins[i][2:]:
                num_bins[i-1:i+1] = [(num_bins[i-1][0],num_bins[i][1],num_bins[i-1][2]+num_bins[i][2],num_bins[i-1][3]+num_bins[i][3])]
                break
        else:
            break
    #计算WOE
    def get_woe(num_bins):
        columns = ["min","max","count_0","count_1"]
        df = pd.DataFrame(num_bins,columns=columns)
        df["total"] = df.count_0 + df.count_1
        df["good%"] = df.count_0/df.count_0.sum()
        df["bad%"] = df.count_1/df.count_1.sum()
        df["woe"] = np.log(df["good%"] / df["bad%"])
        return df
    #计算IV值
    def get_iv(df):
        rate = df["good%"] - df["bad%"]
        iv = np.sum(rate * df.woe)
        return iv
    # 卡方检验，合并分箱
    IV = []
    axisx = []
    while len(num_bins) > n:
        global bins_df
        pvs = []
        for i in range(len(num_bins)-1):
            x1 = num_bins[i][2:]
            x2 = num_bins[i+1][2:]
            pv = scipy.stats.chi2_contingency([x1,x2])[1]
            pvs.append(pv)
        i = pvs.index(max(pvs))
        num_bins[i:i+2] = [(num_bins[i][0],num_bins[i+1][1],num_bins[i][2]+num_bins[i+1][2],num_bins[i][3]+num_bins[i+1][3])]
        bins_df = pd.DataFrame(get_woe(num_bins))
        axisx.append(len(num_bins))
        IV.append(get_iv(bins_df))
        
    if graph:
        plt.figure()
        plt.plot(axisx,IV)
        plt.xticks(axisx)
        plt.xlabel("number of box")
        plt.ylabel("IV")
        plt.show()
        
    return bins_df

 

for i in model_data.columns[1:-1]:
    print(i)

    graphforbestbin(model_data,i ,"SeriousDlqin2yrs",n=2,q = 20)

 

.

.

.

# 根据图像观察手动把特征进行最佳分箱操作
# 特征名称：分箱的个数/箱子的转折点
auto_bins = {'RevolvingUtilizationOfUnsecuredLines':5
            ,'age':6
            ,'DebtRatio':4
            ,'MonthlyIncome':3
            ,'NumberOfOpenCreditLinesAndLoans':7
            }


# 手动处理对于不能分箱的特征
hand_bins = {'NumberOfTime30-59DaysPastDueNotWorse':[0,1,2,13]
            ,'NumberOfTimes90DaysLate':[0,1,2,17]
            ,'NumberRealEstateLoansOrLines':[0,1,2,4,54]
            ,'NumberOfTime60-89DaysPastDueNotWorse':[0,1,2,8]
            ,'NumberOfDependents':[0,1,2,3]
            }
#用np.-inf , np.inf
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}

bins_of_col = {}
for col in auto_bins:
    bins_df = graphforbestbin(model_data,col,'SeriousDlqin2yrs',n = auto_bins[col],q=20,graph=False)
    bins_list = sorted(set(bins_df['min']).union(bins_df['max']))
    bins_list[0],bins_list[-1] = -np.inf,np.inf
    bins_of_col[col] = bins_list

bins_of_col.update(hand_bins)
bins_of_col 

 

4.4 计算各箱的WOE并映射到数据

data = model_data.copy() 
data = data[["age","SeriousDlqin2yrs"]].copy() 
  
data["cut"] = pd.cut(data["age"],[-np.inf, 36.0, 52.0, 56.0, 61.0, 74.0, np.inf]) 
# 不同的年龄段/箱子对于的年龄和标签 


data.groupby("cut")["SeriousDlqin2yrs"].value_counts() 
  
#使用unstack()来将分支状结构变成表状结构 
data.groupby("cut")["SeriousDlqin2yrs"].value_counts().unstack() 
  
bins_df = data.groupby("cut")["SeriousDlqin2yrs"].value_counts().unstack() 
  
bins_df["woe"] = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum())) 
  

 

对所有的特征进行计算箱子的WOE

# df:数据表
# col：列
# bins：箱子的个数
def get_woe(df,col,y,bins):
    
    df = df[[col,y]].copy()
    df["cut"] = pd.cut(df[col],bins) 
    bins_df = df.groupby("cut")[y].value_counts().unstack()
    woe = bins_df["woe"] = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
    iv = np.sum((bins_df[0]/bins_df[0].sum()-bins_df[1]/bins_df[1].sum())*bins_df['woe'])
    return woe


# 所有的WOE
woeall = {}

for col in bins_of_col:
    woeall[col] = get_woe(model_data,col,"SeriousDlqin2yrs",bins_of_col[col])
woeall   

model_woe = pd.DataFrame(index=model_data.index)

for col in bins_of_col:
    model_woe[col] = pd.cut(model_data[col],bins_of_col[col]).map(woeall[col])

model_woe["SeriousDlqin2yrs"] = model_data["SeriousDlqin2yrs"]

model_woe  #这就是建模数据

4.5 建模与模型验证

woeall_vali = {}
for col in bins_of_col:
    woeall_vali[col] = get_woe(vali_data,col,"SeriousDlqin2yrs",bins_of_col[col])
    
# 测试数据    
vali_woe = pd.DataFrame(index=vali_data.index)
for col in bins_of_col:
    vali_woe[col] = pd.cut(vali_data[col],bins_of_col[col]).map(woeall_vali[col])

vali_woe["SeriousDlqin2yrs"] = vali_data["SeriousDlqin2yrs"]


vali_x = vali_woe.iloc[:,:-1]
vali_y = vali_woe.iloc[:,-1]


from sklearn.linear_model import LogisticRegression as LR
# 训练集
x = model_woe.iloc[:,:-1]
y = model_woe.iloc[:,-1]
lr = LR().fit(x,y)
lr.score(vali_x,vali_y)

 

• C是正则化强度的倒数，C越小，损失函数就越小，模型对损失函数的惩罚越重
• solver：默认是liblinear，针对小数据量是个不错的选择，用于求解使模型最优化参数的算法，即最优化问题的算法
• max_iter：所有分类的实际迭代次数，对于liblinear求解器，会给出最大的迭代次数

c_1 = np.linspace(0.01,1,20) 
c_2 = np.linspace(0.01,0.2,20)

score = []
for i in  c_1:
    lr = LR(solver="liblinear",C = i).fit(x,y)
    score.append(lr.score(vali_x,vali_y))


plt.figure()
plt.plot(c_1,score)
plt.show()

 

import warnings
warnings.filterwarnings('ignore')
score = []
for i in [1,2,3,4,5,6]:
    lr = LR(solver="liblinear" ,C = 0.025 , max_iter=i).fit(x,y)
    score.append(lr.score(vali_x , vali_y))
    
plt.figure()
plt.plot([1,2,3,4,5,6],score)
plt.show()

 

import scikitplot as skplt  #pip install scikit-plot 
  
vali_proba_df = pd.DataFrame(lr.predict_proba(vali_x))

skplt.metrics.plot_roc(vali_y, vali_proba_df, plot_micro=False,figsize=(6,6),plot_macro=False) 

 

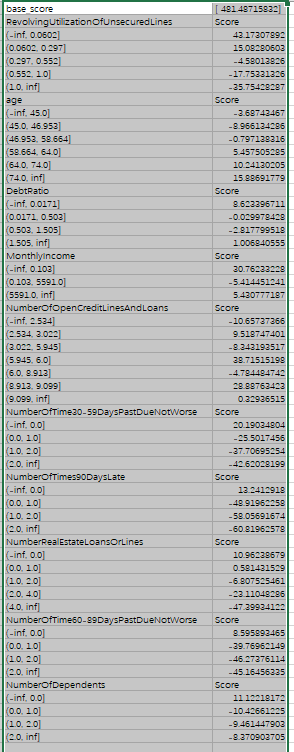
4.6 制作评分卡

• 评分卡中的分数，由以下公式计算：Score = A - B *log(odds)
• A与B是常数，A叫做“补偿”，B叫做“刻度

• log(odds)代表了一个人违约的可能性,逻辑回归的结果取对数几率形式会得到θX，即参数*特征矩阵，所以log(odds)其实就是参数。两个常数可以通过两个假设的分值带入公式求出，这两个假设分别是：
  • 某个特定的违约概率下的预期分值
  • 指定的违约概率翻倍的分数（PDO）

• 例如，假设对数几率为1/60时,设定的特定分数为600，PDO=20，那么对数几率为1/30时的分数就是620。带入以上线性表达式，可以得到：
  • 600 = A - B*log(1/60)
  • 620 = A - B*log(1/30)

B = 20/np.log(2) 
A = 600 + B*np.log(1/60)

base_score = A - B*lr.intercept_ 
base_score

lr.coef_[0][1]*B # log(odds)

score_age = woeall["age"] * (-B*lr.coef_[0][0]) 



file = "ScoreData.csv" 
with open(file,"w") as fdata:
    fdata.write("base_score,{}
".format(base_score))
for i,col in enumerate(x.columns):
    score = woeall[col] * (-B*lr.coef_[0][i])
    score.name = "Score"
    score.index.name = col
    score.to_csv(file,header=True,mode="a")

 

最终打分结果 ：