【CLJ】
- 所谓的“持久化数据结构”,就是保存这个数据结构的所有历史版本,同时利用它们之间的共用数据减少时间和空间的消耗。
【Regina】
- 主席树是一种离线数据结构,是由很多棵线段树组成的。
- 第i棵线段树存的是前i个数的信息:
每一个线段存数字的出现次数(因此建树之前要离散化)。
- n棵线段树会MLE。
但是我们发现第i棵线段树和第i-1棵线段树是非常相似的,有许多结点完全相同,因此可以借用之前的结点,没必要新建结点。
- 建树方法建下图:
(看看图基本上就能理解了)
序列为 4 1 3 2(离散之后,数字是大小排名)
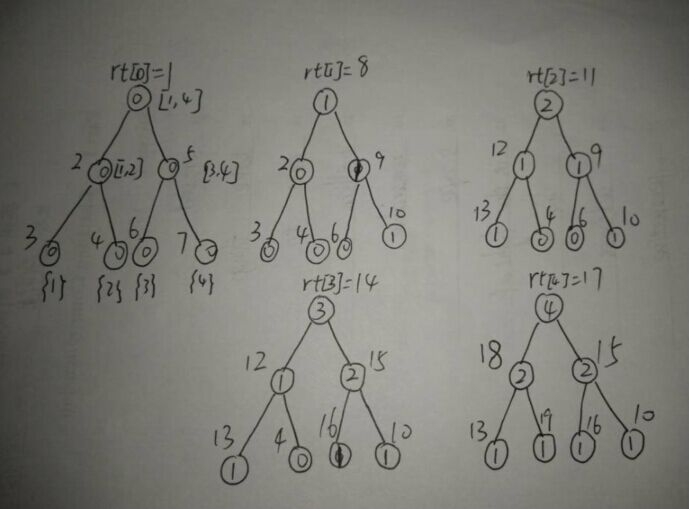
【图一】:看编号,我们发现圆圈里值发生变化时,会产生新的编号(即新的节点)。
即每次最多新产生logn个节点,空间就是省在了整理。
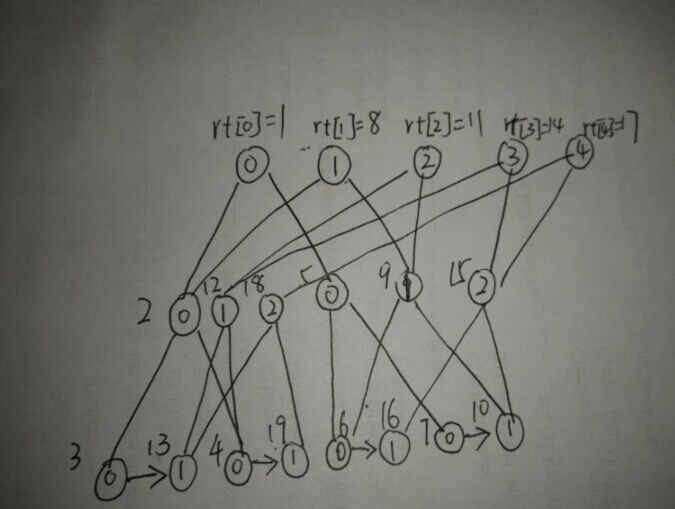
【图二】:结果就产生了这样一棵树,这棵树可以前缀和操作。
- 那么如果要询问i-j之间数字出现的次数怎么办呢?
因为每一棵线段树的区间都是相同的,所以要求l-r之间的数字的出现次数只要用前r位出现的次数减去前l-1位出现的次数,就是ans
- 但是如果有修改操作怎么办?
- 如果沿用上面的做法,那么修改操作是O(nlogn)的,查询是O(1)的,修改要花好长时间。。。
前缀和联想到了树状数组,那么将前缀和用树状数组维护的话修改是O(logn*logn),查询时O(logn),查询的时间虽然变长,但是修改的时间缩短许多!!
注意:
- 函数式线段树的数组要开大一点!!
【参考】