【转】链式前向星基本原理

以下转载自https://blog.csdn.net/qq_41754350/article/details/81082728

一、概述

　　我们在学习图论的时候学习了一种图的存储结构--二维数组邻接矩阵储存，他虽然可以表达直观，快速访问连接两点的边，但是它占用空间大，只适用于点少的图，所以我们需要一种能够可以存储大型图的东西--链式前向星。

      前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,并记录下以某个点为起点的所有边在数组中的起始位置和存储长度。

二、链式前向星基本原理

首先我们要存入以下一张图：

 

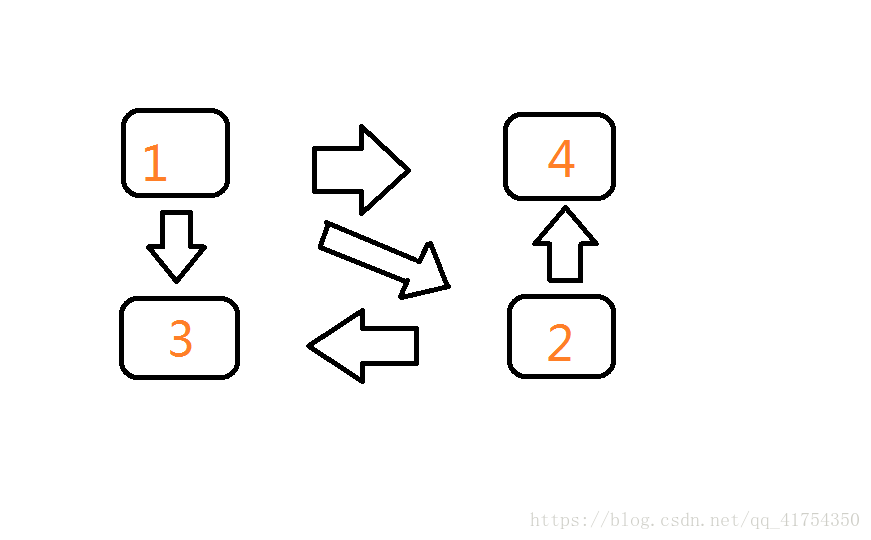
点1指向点2、点3、点4。

  链式前向星是以边为主的存图方式，我们需要利用结构体来规划边，这会使图变得更加清晰。

  首先我们需要建立边的数组edge[ ]，一般我们需要它记录多种元素：下一条边的编号，这条边到达的点，这条边的长度 

struct Edge
{
int next;//下一条边的编号 
int to;//这条边到达的点 
int dis;//这条边的长度 
}edge[maxm];

 

其次我们将已知的边加入； 

int main()
{
num_edge=0;//定义边数，后面直接++ 
scanf("%d%d",&n,&m);//输入点数和边数
for(int i=1;i<=m;i++)//记录边数 
{
scanf("%d%d%d",&u,&v,&d);//输入从哪里来到哪里去权值是多少 
add_edge(u,v,d);//正存图 
add_edge(v,u,d);//如果是无向图，就要反存图 
}    

}

 

我们可以添加一个add函数方便我们添加：

void add_edge(int from,int to,int dis) //加入一条从from到to距离为dis的单向边 
{
edge[++num_edge].next=head[from]; 
edge[num_edge].to=to;//将to记录 
edge[num_edge].dis=dis;//将dis记录 
head[from]=num_edge;// 
}

 

可能过这一步有点迷，下面是一个存图的模拟：

 

 

这边模拟走完后，可以得到以下图：

 

 

突发奇想，可能这样比较形象： 

 

 

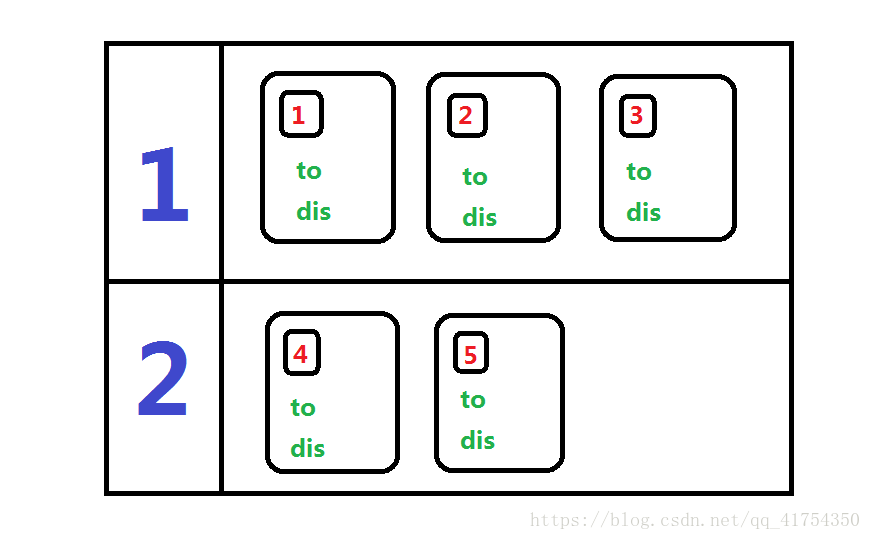
最后一部就是调用，它根据你的题目来决定。但都离不开以下程序核心：

for(int i=head[k];i!=0;i=edge[i].next)

 以上转载自https://blog.csdn.net/qq_41754350/article/details/81082728