关于可持久化锯树结构
这个东西,看起来就很持久
就是记录历史版本的数据结构,但是衍生出的作用就很多,下面来康康吧
可持久化线段树(主席树)
首先,这是一棵可爱且正常的线段树
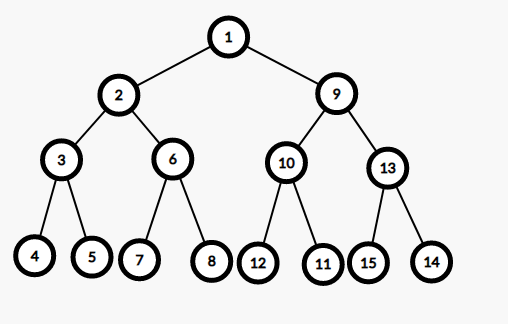
如果我们要更改一个节点,那我们就要更改这个节点以上的所有节点(因为有时候可能信息向上传递也会改)
然后这就是恶心的主席树
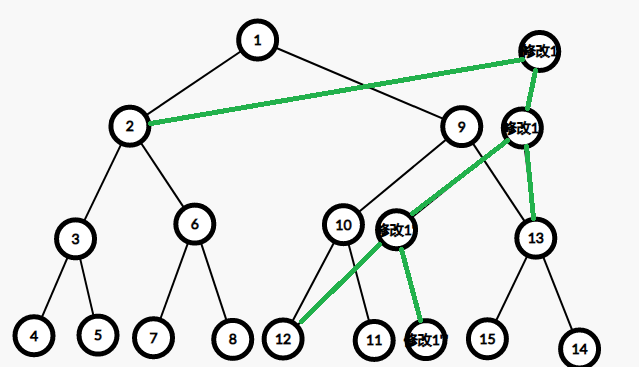
所以每一次更改我们都需要重新建一条长度为logn的路线,根节点的编号就可以看做版本编号,其他不变的还是继续连就行了(你也可以每次更改重新建一棵线段树)
这样能极大地节省时间和空间
由此可以看出主席树性质
有很多根
一个节点不止一个父亲
每次更改增加长度为logn
每一个根都是一颗完整的线段树
增加的节点一个连向旧结点,一个连向新结点(除去叶子结点)
那么具体怎么实现呢,来看看吧
实现
首先我们需要一个记录每个版本根结点的数组
int root[M];
建树还是正常建树,但是后来增加的时候要克隆节点信息(因为这样只需要更改一个儿子的信息就可以了)
inline int clone(int p) { ++cnt; t[cnt]=t[p]; return cnt; }
int add(int p,int l,int r,int x,int k) { p=clone(p); if(l==r) { t[p].val=k; return p; } int mid=(l+r)>>1; if(x<=mid)t[p].l=add(t[p].l,l,mid,x,k); else t[p].r=add(t[p].r,mid+1,r,x,k); return p; }
这差不多就是基本的操作了
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1000010; 4 const int M=1000010; 5 int n,m,cnt; 6 struct node{ 7 int l,r,val; 8 }t[N<<4]; 9 struct T{ 10 int root[M]; 11 T(){ 12 memset(root,0,sizeof root); 13 } 14 inline int clone(int p) 15 { 16 ++cnt;//克隆节点 17 t[cnt]=t[p]; 18 return cnt; 19 } 20 int build(int p,int l,int r)//建一棵主树 21 { 22 p=++cnt; 23 if(l==r) 24 { 25 scanf("%d",&t[p].val); 26 return p; 27 } 28 int mid=(l+r)>>1; 29 t[p].l=build(t[p].l,l,mid); 30 t[p].r=build(t[p].r,mid+1,r); 31 return p; 32 } 33 int add(int p,int l,int r,int x,int k)//增加版本 34 { 35 p=clone(p); 36 if(l==r)//更改叶子节点 37 { 38 t[p].val=k; 39 return p; 40 } 41 int mid=(l+r)>>1; 42 if(x<=mid)t[p].l=add(t[p].l,l,mid,x,k); 43 else t[p].r=add(t[p].r,mid+1,r,x,k); 44 return p; 45 } 46 int find(int p,int l,int r,int x)//就是线段树的查找 47 { 48 if(l==r)return t[p].val; 49 int mid=(l+r)>>1; 50 if(x<=mid)return find(t[p].l,l,mid,x); 51 return find(t[p].r,mid+1,r,x); 52 } 53 }tree; 54 int main() 55 { 56 scanf("%d%d",&n,&m); 57 tree.root[0]=tree.build(0,1,n);//记录主树根结点 58 for(int i=1;i<=m;i++) 59 { 60 int r,k,x,y; 61 scanf("%d%d%d",&r,&k,&x); 62 switch(k) 63 { 64 case 1:{ 65 scanf("%d",&y); 66 tree.root[i]=tree.add(tree.root[r],1,n,x,y);//记录版本节点 67 break; 68 } 69 case 2:{ 70 printf("%d ",tree.find(tree.root[r],1,n,x)); 71 tree.root[i]=tree.root[r];//没有更改就是前一个的节点 72 break; 73 } 74 } 75 } 76 return 0; 77 }
区间第K小
这个时候就可以换个方式来理解主席树了——一种前缀和
对于这道题呢,我们前缀和的就是每一个数的个数(当然要从小到大,方便找第k小)
当要取区间L-R的话,我们就可以拿R这一棵去减L-1这一条
(一般都要离散化方便空间)
2 5 4 8 6 2 4 7
假如这个寻找4-7的第k小
那么第2棵和第7棵就是这样的
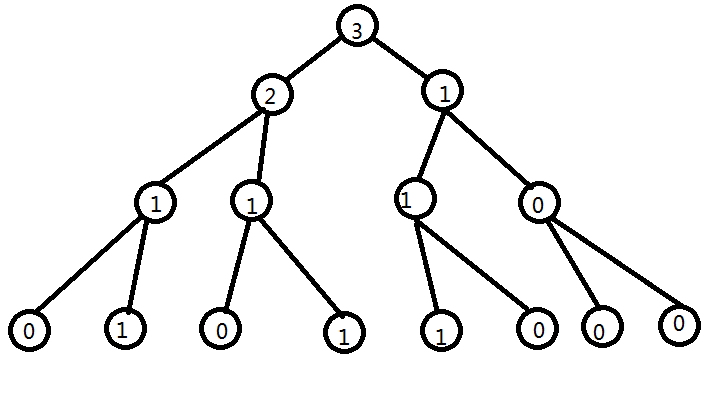
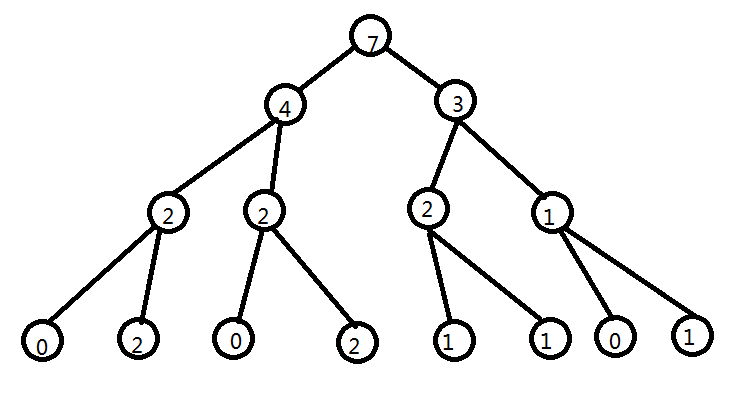
就类似于二分
先比较左端点(其实相减就是区间内的个数了)
如果左边的小于k,说明左边的肯定找不到(因为我们这棵树从左往右是从小到大排序的,如图最下面是1-8的个数)
查找
int find(int p1,int p2,int l,int r,int k) { if(l==r)return l; int mid=(l+r)>>1; int x=t[t[p2].l].sum-t[t[p1].l].sum; if(x>=k)return find(t[p1].l,t[p2].l,l,mid,k); return find(t[p1].r,t[p2].r,mid+1,r,k-x); }
剩下建树其实都还是一样的,但是我介绍一种不一样的建树方法,不是在原来上面建
合并线段树
之前是直接加上去,但是可以单独建一棵类似长度为logN的链
合并线段树主要涉及的是动态开点的线段树——就是说用到哪个点就开到哪个点,这样的话能极大地节省空间(当然,这道题开了的都有数,所以并不能优化很多)
增加
int add(int p,int l,int r,int k) { p=++cnt;//新建节点,这里就不是复制原来的节点了 t[p].sum++;//因为只有最底部增加了一个数,所以整条链如果要更新信息的话就是1 if(l==r)return p; int mid=(l+r)>>1; if(k<=mid)t[p].l=add(t[p].l,l,mid,k);//向下新建节点 else t[p].r=add(t[p].r,mid+1,r,k); return p; }
合并
int merge(int x,int y) { if(!x||!y)return x|y;//如果有其中一个的节点为空,就可以直接返回 int p=++cnt; t[p].sum=t[x].sum+t[y].sum;//否则新建节点合并信息 t[p].l=merge(t[x].l,t[y].l); t[p].r=merge(t[x].r,t[y].r); return p; }
代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=200010; 4 const int M=200010; 5 int n,m,bn,cnt; 6 int a[N],b[N]; 7 struct node{ 8 int l,r,sum; 9 }t[N<<5]; 10 struct tree{ 11 int root[N]; 12 tree(){ 13 memset(root,0,sizeof root); 14 } 15 int build(int p,int l,int r)//建主树 16 { 17 p=++cnt; 18 if(l==r)return p; 19 int mid=(l+r)>>1; 20 t[p].l=build(t[p].l,l,mid); 21 t[p].r=build(t[p].r,mid+1,r); 22 return p; 23 } 24 int add(int p,int l,int r,int k)//新建 25 { 26 p=++cnt; 27 t[p].sum++; 28 if(l==r)return p; 29 int mid=(l+r)>>1; 30 if(k<=mid)t[p].l=add(t[p].l,l,mid,k); 31 else t[p].r=add(t[p].r,mid+1,r,k); 32 return p; 33 } 34 int merge(int x,int y)//合并 35 { 36 if(!x||!y)return x|y; 37 int p=++cnt; 38 t[p].sum=t[x].sum+t[y].sum; 39 t[p].l=merge(t[x].l,t[y].l); 40 t[p].r=merge(t[x].r,t[y].r); 41 return p; 42 } 43 int find(int p1,int p2,int l,int r,int k)//查找 44 { 45 if(l==r)return l; 46 int mid=(l+r)>>1; 47 int x=t[t[p2].l].sum-t[t[p1].l].sum; 48 if(x>=k)return find(t[p1].l,t[p2].l,l,mid,k); 49 return find(t[p1].r,t[p2].r,mid+1,r,k-x); 50 } 51 }T; 52 int main() 53 { 54 scanf("%d%d",&n,&m); 55 for(int i=1;i<=n;i++) 56 scanf("%d",&a[i]),b[i]=a[i]; 57 sort(b+1,b+1+n); 58 bn=unique(b+1,b+1+n)-b-1;//去重排序 59 for(int i=1;i<=n;i++) 60 T.root[i]=T.add(T.root[i],1,bn,lower_bound(b+1,b+1+bn,a[i])-b);//新建 61 for(int i=2;i<=n;i++)T.root[i]=T.merge(T.root[i-1],T.root[i]);//合并 62 while(m--) 63 { 64 int x,y,k; 65 scanf("%d%d%d",&x,&y,&k); 66 printf("%d ",b[T.find(T.root[x-1],T.root[y],1,bn,k)]);//输出 67 } 68 return 0; 69 }
可持久化01字典树
前置知识
01字典树
我们都知道一般用来解决最大异或和的问题(不知道的先去做普通的),但是这里是和前面所有的异或,万一涉及到一个区间里的最大异或怎么办呢
很容易能想到前缀和来求区间,自然而然就是我们可持久化的利用啦!(和前面第k小主席树思路大致相同,都是拿树减树
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=6e5+10; 4 int n,m,r; 5 int a[3*N]; 6 struct node{ 7 int ch[2]; 8 int num; 9 }t[N*40]; 10 inline int read() 11 { 12 int x=0,f=1; 13 char ch=getchar(); 14 while(ch<'0'||ch>'9'){ 15 if(ch=='-') 16 f=-1; 17 ch=getchar(); 18 } 19 while(ch>='0'&&ch<='9'){ 20 x=(x<<1)+(x<<3)+(ch^48); 21 ch=getchar(); 22 } 23 return x*f; 24 } 25 struct tree{ 26 int root[N]; 27 int cnt; 28 tree(){ 29 memset(root,0,sizeof root); 30 cnt=0; 31 } 32 int clone(int p)//复制节点 33 { 34 ++cnt; 35 t[cnt]=t[p]; 36 return cnt; 37 } 38 int add(int p,int x ,int d)//新建节点 39 { 40 p=clone(p); 41 t[p].num++; 42 if(d==-1)return p; 43 bool k=(x>>d)&1; 44 t[p].ch[k]=add(t[p].ch[k],x,d-1); 45 return p; 46 } 47 int find(int f1,int f2,int x,int d)//找最大值 48 { 49 if(d==-1)return 0; 50 bool k=(x>>d)&1; 51 int ans=0; 52 if(t[t[f2].ch[!k]].num>t[t[f1].ch[!k]].num)ans+=(1<<d),ans+=find(t[f1].ch[!k],t[f2].ch[!k],x,d-1); 53 else ans+=find(t[f1].ch[k],t[f2].ch[k],x,d-1); 54 return ans; 55 } 56 }T; 57 int main() 58 { 59 n=read(),m=read(); T.root[r] = T.add(0,a[r],25);//一定要新建空的树 60 for(r=1;r<=n;r++) 61 { 62 a[r]=read(); 63 a[r]^=a[r-1]; 64 T.root[r]=T.add(T.root[r-1],a[r],25); 65 } 66 r--; 67 while(m--) 68 { 69 char k[3]; 70 int l,R,x; 71 scanf("%s",k); 72 switch(k[0]) 73 { 74 case 'A':{ 75 ++r; 76 a[r]=read(); 77 a[r]^=a[r-1]; 78 T.root[r]=T.add(T.root[r-1],a[r],25); 79 break; 80 } 81 case 'Q':{ 82 l=read(),R=read(),x=read(); 83 x^=a[r]; 84 if(l==1)printf("%d ",T.find(0,T.root[R-1],x,25)); 85 else printf("%d ",T.find(T.root[l-2],T.root[R-1],x,25)); 86 break; 87 } 88 } 89 } 90 return 0; 91 }
可持久化并查集
说是并查集,其实和并查集没啥关系,还是用的主席树来实现,我们记录每个点的父亲节点,可见每次更改只更改一个点的父亲节点,所以有很多相同的地方(可持久化的目的就是利用相同的地方节省空间)
注意,这里我们不用路径压缩,因为这样的话一次不止更改一个点,MLE++,TLE++,但是万一退化成链怎么办呢,那就用启发式合并来解决这个问题!
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=200010; 4 const int M=200010; 5 int n,m,cnt; 6 struct node{ 7 int l,r,fa,deep; 8 }t[N*60]; 9 struct tree{ 10 int root[M]; 11 tree(){ 12 memset(root,0,sizeof root); 13 } 14 int clone(int p) 15 { 16 ++cnt; 17 t[cnt]=t[p]; 18 return cnt; 19 } 20 int build(int p,int l,int r) 21 { 22 p=++cnt; 23 if(l==r) 24 { 25 t[p].fa=l; 26 return p; 27 } 28 29 int mid=(l+r)>>1; 30 t[p].l=build(0,l,mid); 31 t[p].r=build(0,mid+1,r); 32 return p; 33 } 34 int find(int p,int l,int r,int x)//查找父亲节点 35 { 36 if(l==r)return t[p].fa; 37 int mid=(l+r)>>1; 38 if(x<=mid)return find(t[p].l,l,mid,x); 39 return find(t[p].r,mid+1,r,x); 40 41 } 42 void add(int p,int l,int r,int x)//增加深度 43 { 44 if(l==r) 45 { 46 t[p].deep++; 47 return ; 48 } 49 int mid=(l+r)>>1; 50 if(x<=mid)add(t[p].l,l,mid,x); 51 else add(t[p].r,mid+1,r,x); 52 return; 53 } 54 int ask(int p,int x) //一直查找到根节点 55 { 56 int f=find(p,1,n,x); 57 if(x==f)return f; 58 return ask(p,f); 59 } 60 int update(int p,int l,int r,int f1,int f2)//更改节点 61 { 62 p=clone(p); 63 if(l==r) 64 { 65 t[p].fa=f2; 66 return p; 67 } 68 int mid=(l+r)>>1; 69 if(f1<=mid)t[p].l=update(t[p].l,l,mid,f1,f2); 70 else t[p].r=update(t[p].r,mid+1,r,f1,f2); 71 return p; 72 } 73 }T; 74 int main() 75 { 76 scanf("%d%d",&n,&m); 77 T.root[0]=T.build(0,1,n);//初始化 78 for(int i=1;i<=m;i++) 79 { 80 int opt,a,b,k; 81 scanf("%d",&opt); 82 switch(opt) 83 { 84 case 1:{//更改父亲节点 85 T.root[i]=T.root[i-1]; 86 scanf("%d%d",&a,&b); 87 int f1=T.ask(T.root[i-1],a); 88 int f2=T.ask(T.root[i-1],b); 89 if(f1==f2)continue; 90 if(t[f1].deep>t[f2].deep)swap(f1,f2);//启发式合并,把深度小的合到深度大的 91 T.root[i]=T.update(T.root[i-1],1,n,f1,f2); 92 T.add(T.root[i],1,n,f2); 93 break; 94 } 95 case 2:{//回溯 96 scanf("%d",&k); 97 T.root[i]=T.root[k]; 98 break; 99 } 100 case 3:{//询问 101 scanf("%d%d",&a,&b); 102 T.root[i]=T.root[i-1]; 103 int f1=T.ask(T.root[i],a); 104 int f2=T.ask(T.root[i],b); 105 if(f1==f2)puts("1"); 106 else puts("0"); 107 break; 108 } 109 } 110 } 111 return 0; 112 }