所谓非线性结构,是指在该类结构中至少存在一个数据元素,它具有两个或者两个以上的直接前驱或直接后驱。树型结构就是一种非常重要且应用广泛的非线性结构。

树的定义:
树是N(N>= 0)个节点的有限集合。它满足如下条件
1.有一个特殊的节点称为根节点(Root)
2.除根结点之外的其余节点可分为m(m>=0)个互不相交的有限集合:T1、T2、T3、T4、T5...,其中每一个集合本身又是一棵树,并且称为根的子树
3.特别地,可以允许不包括任何节点地树,把它称为空树。只有一个节点地树称为最小树
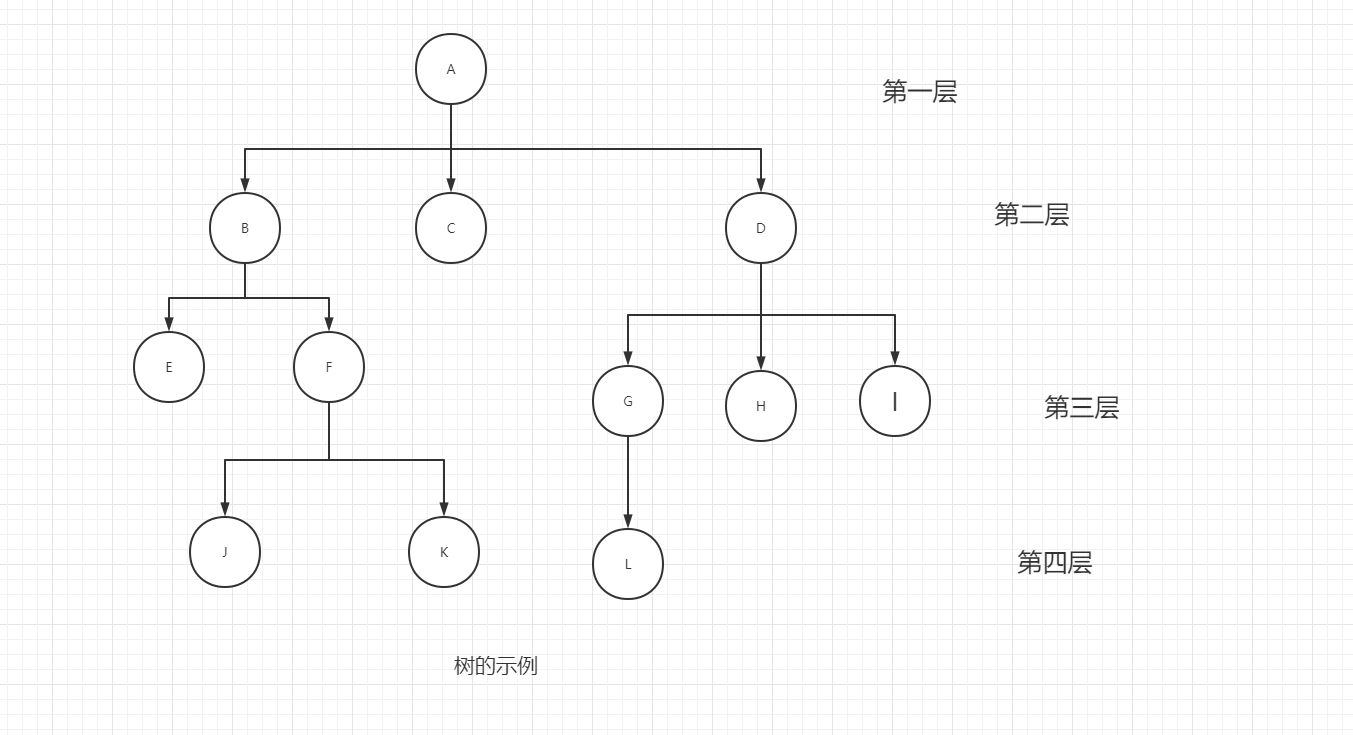
如下图所示是一个具有12个节点地树,其中节点A是根,其余节点又可分为互不相交地结点子集
T1 = {B,E,F,J,K}
T2 = {C}
T3 = {D,G,H,I,L}
T1 T2 T3都是根A的子树,且它们本身也是一棵树,例如T1,根节点是B,其余节点为
T11 = {E}
T12 = {F,G,K}
T11 是只有一个根节点的树,没有子树。值得注意的是每棵子树是绝对不能相交的,否则就不能构造一棵递归定义的树
树的特点:
在一棵树中,通常将一个节点定义为其子树的根结点的前驱节点,而其子树的根结点就是它的后继节点。因此从逻辑上看,树型结构具有以下特点:
1.树的根节点没有前驱节点,除了根节点之外的所有节点都有且仅有一个前驱节点
2.树中所有节点可以有零个或多个后继节点
树的基本术语
1.节点:树型结构里面的元素
2.子树:当节点大于1时,其余的节点分为互不相交的集合称为子树
3.度:一个节点拥有子树的数量称为节点的度
4.叶子:度为0的节点
5.孩子:节点的子树的根称为孩子节点
6.双亲:该节点成为孩子的双亲
7.兄弟:同一个双亲节点
8.深度:节点的最大层次成为树的深度
9.森林:由m个互不相交的树的集合
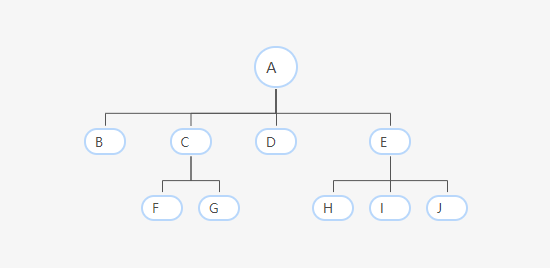
1.叶子节点有:B D F G H I J
2.非终端节点有:A C E
3.A的度为4,C的度为2,E的度为3 其余节点的度为0
4.树的深度为3