1 为什么需要jstl?
jsp中常常使用EL和jstl来实现无脚本,上次说到el(expression language)。这种表达式语言主要是获取属性和参数,获取四大作用域的属性(pagecontent,request,session,application)和request,cookie中的参数,值得一提的是:不能过使用el赋值。el理解起来比较简单,不足之处就是功能有限。那么怎么实现for语句,if等语句;设置四大作用域的属性等等功能
2 jstl介绍
为了jsp支持jstl,我们需要下载二个jar包(jstl.jar,standard.jar)。jstl有5个库,这里介绍通用的核心库(其他是专用)。jstl全称jsp standard tag library,jsp标准标记库。这些库是事先定义好的,企业或者个人可以设计一套自己的库(自定义标记库)。这里先介绍核心库
(1)实现for语句,标记<C:forEach>

看上面的图一目了然,需要注意,第一:var里面的变量名不等价于i;第二点:items里面可以集合(list,map)或者数组;第三var作为属性保存在pagecontent中
(2)if语句<c:if>
格式: <c:if test="条件"></c:if>
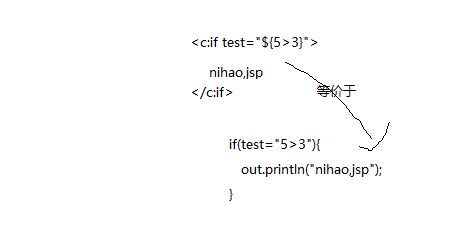
(3) 怎么没有else?

(4)厉害了,我的set <c:set>
@set:使用var设置属性,看图
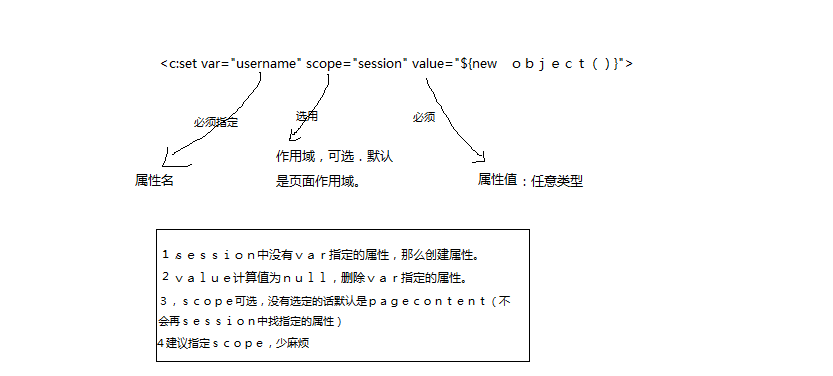
@set:使用target设置bean或者map的值

注意:target为null,或者property为null,都会抛出异常
(5)删除属性<c:remove>
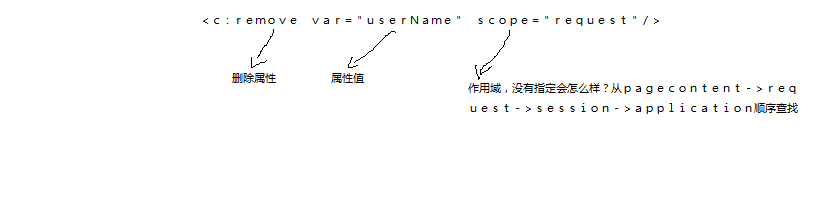
(6)页面包含<c:import>
我们之前知道2种方法可以将页面包含进来;
第一种:指令<%@include file="header.jsp"%>
第二种:动作<jsp:include page="header.jsp">
现在说说第三种:

<c:param name="title" value="this is andy‘s jsp">是为request设置一个参数,可以在头页面显示"自己的东西"
(7)了不起的<c:url>
为什么说了不起?原因是他可以用来重写url。客户端禁止使用cookie时浏览器无法识别set:cookie首部。导致session不能正常工作,此时只有一条后路->重写url(将JessionId添加到url后面)。假如客户端禁止使用cookie,jsp中我们可以用<c:url>设置链接(有重写功能)。你不懂cookie(Jsessionid)?难理解。懂?那就明白了。其实我应该也会写这方面的总结。
(8)其他
这里就不再介绍更多了,我们可以去查jstl文档获取更多的知识
-----------------------------------------------------------------------------------------------------------------------------------------
jstl是事先为我们(开发人员)准备好的标准库,那么可以创建企业或者个人的库吗(tld文件,处理器是关键)。