学习目标:抓住80%的核心考点 (参考专业综合考试大纲一书)
重点如下:
1概率论知识(同大学课程):计算均值,方差,标准差,背公式,正态分布
2统计量及抽样分布-核心知识
3参数估计(计算题) -居间估计计算
4假设检验(判断题)
5线性回归方程(小题)-判断相关性
6other:其他是非重点
------------------------------开始扯淡-----------------------------
1变量分类:(后期分析的变量都将针对这三类变量)
分类变量(categorical variable) :说明事物类别的名称
顺序变量(rank variable):说明事物有序类别的名称
数值型变量(metric variable) :说明事物数字特征的名称
2基本概念:
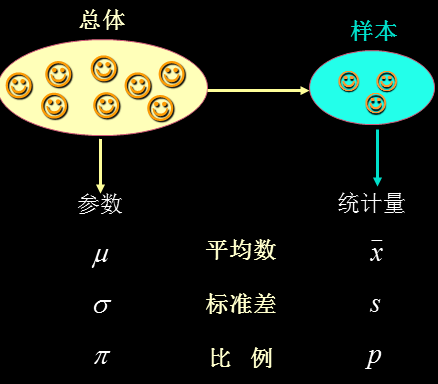
后期在计算时,要区别研究对象是整体还是样本,这样计算公式带入的参数不一样。
3数据度量
a 集中趋势:一组数据向其中心值靠拢的倾向和程度
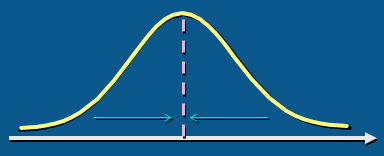
分类数据:众数 (出现次数最多)
顺序数据:中位数(排序后处于中间位置上的值)和四分位数(排序后处于25%和75%位置上的值)
数值型数据:平均数(均值)-如上图
三者关系如下图:
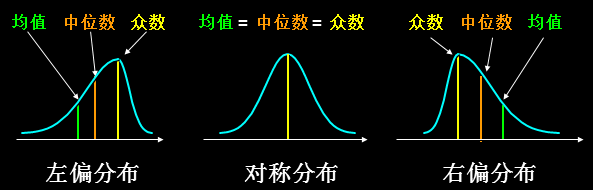
b 离散程度(反映各变量值远离其中心值的程度)
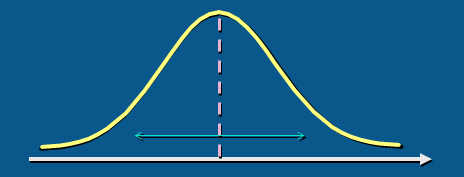
分类数据:异众比率 (用于衡量众数的代表性)
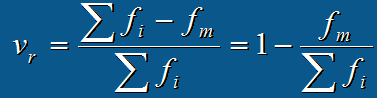
顺序数据:四分位差(反映了中间50%数据的离散程度)

数值型数据:方差和标准差 (大学概率论知识)-这里的X- 用u代替则是-总体方差和标准差

相对离散程度:离散系数(用于对不同组别数据离散程度的比较)
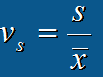
----------------------------------以下是概率论知识:重点是正态分布----------------------------------------------
1离散型随机变量:
数学期望计算:![]()
方差计算:
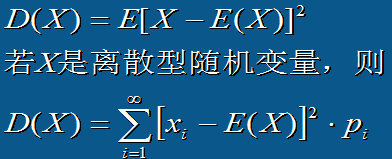
常见的离散型随机变量:二项分布(非0即1)
2连续随机变量:
概率密度函数:相当于高数的积分函数(总体面积为1)
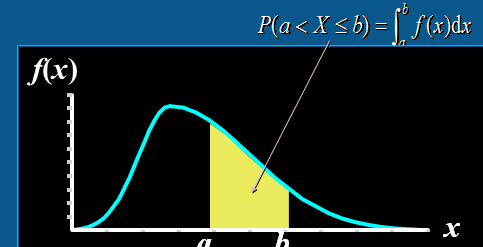
分布函数:相当于上图的a-b部分的面积
正态分布:(标准正态分布有对称性)

-------------------------------------------以下是统计学基础知识-------------------------------------------------------
1统计量:是样本的一个函数,是函数,是函数,重要的说三次。
2 .X2分布:期望为n,方差为2n(n为自由度) (n决定分布的形状,通常是不对称的正偏分布,当n增加时,形状趋于对称)
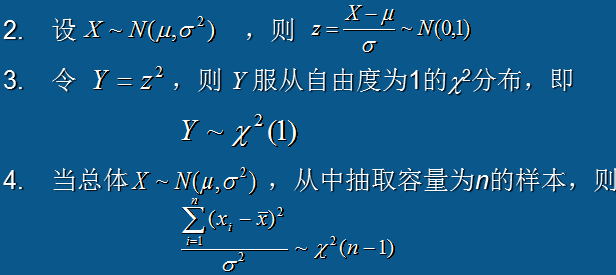
t分布:类似正态分布的一种对称分布,它通常要比正态分布平坦和分散 (所以后面的参数估计计算中,用t分布计算出来的值和正态分布相差不大)
F分布:(就是两个自由度的x2分布合在一起的)

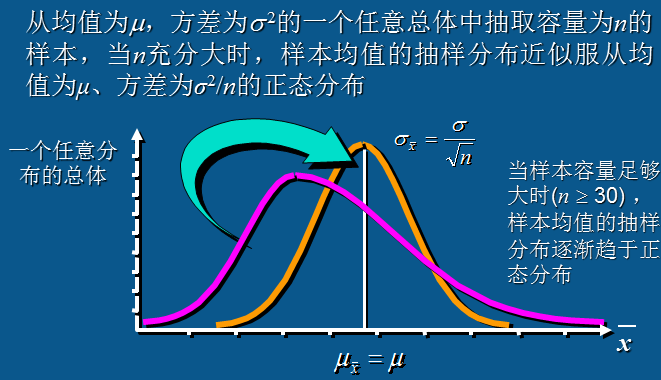
中心极限定理(就是他们在N样本量很大时,都会服从标准正态分布-为了简化计算吧,偷懒)
-------------------------------------------------------END-----------------------------------------------------------------------