对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列——来源百度百科;
如果定义较为抽象,我们举个非常通用的例子,我看过的大部分博客都是举得这个例子:选课
一个计算机专业的学生必须完成图3-4所列出的全部课程。在这里,课程代表活动,学习一门课程就表示进行一项活动,学习每门课程的先决条件是学完它的全部先修课程。如学习《数据结构》课程就必须安排在学完它的两门先修课程《离散数学》和《算法语言》之后。学习《高等数学》课程则可以随时安排,因为它是基础课程,没有先修课。若用AOV网来表示这种课程安排的先后关系,则如图3-5所示。图中的每个顶点代表一门课程,每条有向边代表起点对应的课程是终点对应课程的先修课。图中的每个顶点代表一从图中可以清楚地看出各课程之间的先修和后续的关系。如课程C5的先修课为C2,后续课程为C4和C6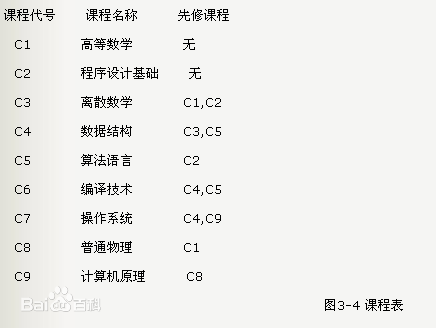
拓扑排序思想:
维护一个入度为0(入度一般指一个点被指向的次数,比如2-4,3-4,4的入度为2)的队列,
循环入度为0的队列,找到循环的点的所有边,某条边指向的点删除这条边的入度为0也加入队列;循环结束的点输出,如果最后输出的点的数量<n,那么有回路;
代码一般有两种:基于dfs和普通模拟过程;