之前写了很多关于Matplotlib的基础知识,这次主要讲一下Matplotlib所生成的几个图:散点图,柱状图,等高线图,图片和3D数据
Scatter散点图
在制作Scatter散点图的过程中,我们首先要引入matplotlib.pyplot简写为plt,再引入模块numpy用来产生一些随机的数据。生成1024个呈正态分布的二维数组(平均数是0,方差是1)作为一个数据集,并图像化这个数据集。其中,每一个点的颜色用T来表示:
import matplotlib.pyplot as plt import numpy as np n=1024 #数据大小 X=np.random.normal(0,1,n) #每一个点的X值 Y=np.random.normal(0,1,n) # T=np.arctan2(Y,X)
数据生成完毕之后,我们需要采用scatter来绘制这些点。在这里,我们输入X和Y作为输入点,颜色为T,color map用作默认值,透明度alpha为50%。X轴显示范围定位为(-1.5,1.5),并用xtick()函数来隐藏x坐标轴,ytick()函数来隐藏y坐标轴
plt.scatter(X,Y,s=75,c=T,alpha=.5) plt.xlim(-1.5,1.5) plt.xticks(()) plt.ylim(-1.5,1.5) plt.yticks(()) plt.show()
综上,该代码最终产生的结果为:
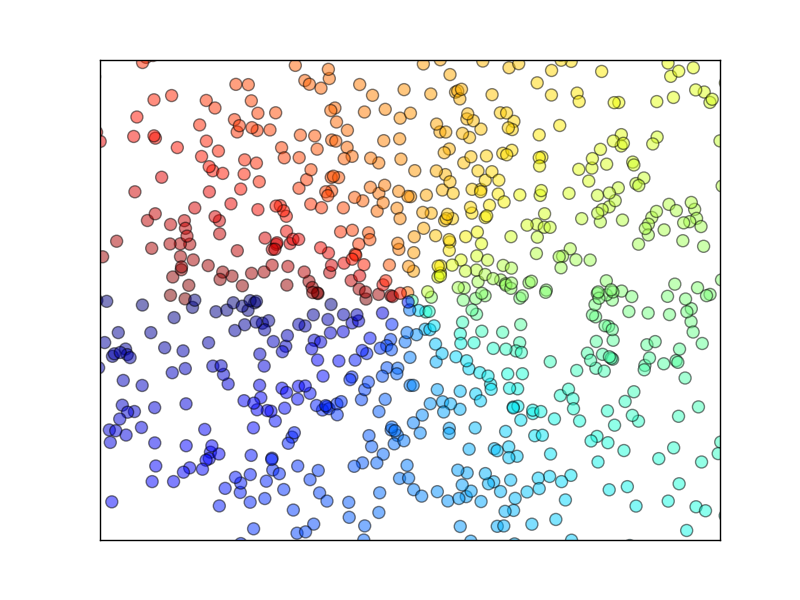
柱状图
在我们平时的机器学习领域中,柱状图通常有很大的作用,它可以很形象的看到趋势的变化。下面就介绍一下如何利用matplotlib来生成一个柱状图。
首先第一步便是生成数据。我们向上向下分别生成12个数据,X为0到11的整数,Y是相应的均匀分布的随机数据。使用的函数是plt.bar,参数是X和Y:
import matplotlib.pyplot as plt import numpy as np n=12 X=np.arange(n) Y1=(1 - X / float(n)) * np.random.uniform(0.5,1.0,n) Y2=(1 - X / float(n)) * np.random.uniform(0.5,1.0,n) plt.bar(X,+Y1) plt.bar(X,-Y2) plt.xlim(-1,n) plt.xticks(()) plt.ylim(-1.25,1.25) plt.yticks(()) plt.show()
这样我们便可以生成柱状图的基本框架。下一步我们需要对该图就颜色和数值进行优化。用facecolor设置主题颜色,edgecolor设置边框颜色。
plt.bar(X,+Y1,facecolor='#9999ff',edgecolor='white') plt.bar(X,-Y2,facecolor='#ff9999',edgecolor='white')
接下来我们用函数plt.text分别在柱体上方(下方)加上数值,用%.2f 保留两位小数,横向居中对齐ha='center',纵向底部(顶部)对齐va='bottom'
for x,y in zip(X,Y1): plt.text(x+0.4,y+0.05,'%.2f' % y,ha='center',va='bottom') for x,y in zip(X,Y2): plt.text(x+0.4,-y-0.05,'%.2f' % y,ha='center',va='bottom')
综上,本部分的所有代码为:
import matplotlib.pyplot as plt import numpy as np n=12 X=np.arange(n) Y1=(1 - X / float(n)) * np.random.uniform(0.5,1.0,n) Y2=(1 - X / float(n)) * np.random.uniform(0.5,1.0,n) plt.bar(X,+Y1,facecolor='#9999ff',edgecolor='white') plt.bar(X,-Y2,facecolor='#ff9999',edgecolor='white') for x,y in zip(X,Y1): plt.text(x+0.4,y+0.05,'%.2f' % y,ha='center',va='bottom') for x,y in zip(X,Y2): plt.text(x+0.4,-y-0.05,'%.2f' % y,ha='center',va='bottom') plt.xlim(-1,n) plt.xticks(()) plt.ylim(-1.25,1.25) plt.yticks(()) plt.show()
所产生的结果为:
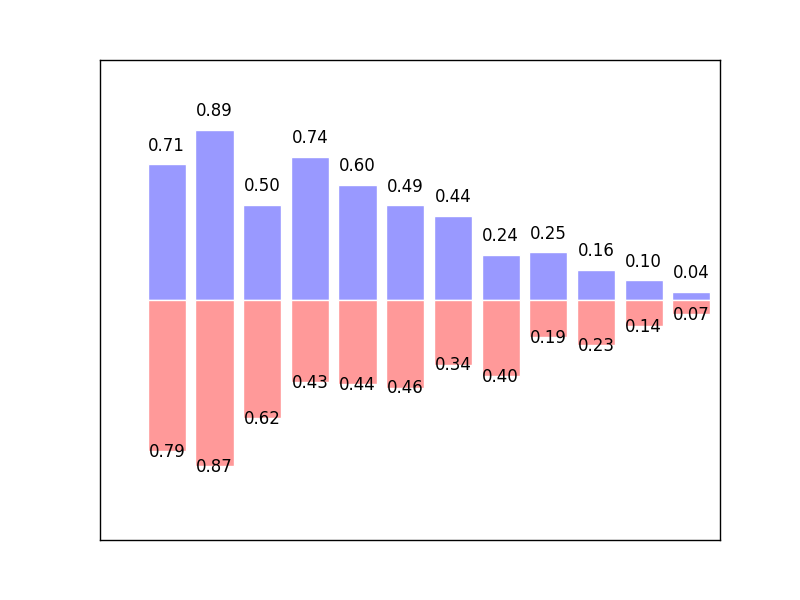
等高线图
在本部分,我们主要介绍如何利用matplotlib生成等高线。在生成等高线中,我们需要三维的数据点:(x,y)和对应的高度。在本程序中,高度我们用一个函数f()来生成。x,y分别是在区间[-3,3]中均匀分布的256个值,并用meshgrid在二维平面中将每一个x和每一个y分别对应起来,编织成栅格:
import matplotlib.pyplot as plt import numpy as np def f(x,y): return (1 - x/2 + x**5 + y**3) * np.exp(-x**2,-y**2) n=256 x=np.linspace(-3,3,n) y=np.linspace(-3,3,n) X,Y=np.meshgrid(x,y)
接下来我们进行颜色填充。使用函数plt.contourf把颜色加进去,位置参数分别为:X,Y,f(X,Y)。透明度0.75,并将f(X,Y)的值对应到color map的暖色组中寻找对应颜色。
plt.contourf(X,Y,f(X,Y),8,alpha=0.75,cmap=plt.cm.hot)
接下来进行等高线绘制。使用plt.contour函数划线。位置参数为 X,Y,f(X,Y)。在我们这里,我们将颜色选为黑色,线条宽度为0.5.现在的结果如下图所示:只有颜色和线条,没有数值Label
C=plt.contour(X,Y,f(X,Y),8,colors='black',linewidth=0.5)
在上面的代码中,我们可以看到,其中的8代表等高线的密集程度,这里被分为10个部分。如果是0,则图像被一分为二。
再下一步,我们需要添加高度数字。我们加入Label,inline控制是否在Label画在线里面,字体大小为10.并将坐标轴隐藏:
plt.clabel(C,inline=True,fontsize=10)
plt.xticks(())
plt.yticks(())
所以,在画等高线的所有代码为:
import matplotlib.pyplot as plt import numpy as np def f(x,y): return (1 - x/2 + x**5 + y**3) * np.exp(-x**2,-y**2) n=256 x=np.linspace(-3,3,n) y=np.linspace(-3,3,n) X,Y=np.meshgrid(x,y) plt.contourf(X,Y,f(X,Y),8,alpha=0.75,cmap=plt.cm.hot) C=plt.contour(X,Y,f(X,Y),8,colors='black',linewidth=0.5) plt.clabel(C,inline=True,fontsize=10) plt.xticks(()) plt.yticks(()) plt.show()
所产生的结果为:

3D数据
在做机器学习的时候,有时候需要绘3D图片来看数据整体的下降趋势。首先在进行3D时除了导入matplotlib,还需要添加一个模块,即3D坐标轴显示,这个包不需要单独安装,python本身就自带的
import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D
之后要定义一个图像窗口,在窗口上添加3D坐标轴。
fig=plt.figure()
ax=Axes3D(fig)
接下来再给出X值和Y值,并将X值和Y值编织成栅格。每一个(X,Y)点对应的高度值,我们用下面这个函数进行计算:
X=np.arange(-4,4,0.25) Y=np.arange(-4,4,0.25) X,Y=np.meshgrid(X,Y) R=np.sqrt(X ** 2 + Y ** 2) Z=np.sin(R)
下一步我们需要做出一个三维曲面,并将一个colormap rainbow填充颜色,之后将三维图像投影到XY平面做一个等高线图。plot 3D 图像:
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=plt.get_cmap('rainbow'))
其中,rstride 和 cstride分别代表row 和 column的跨度
之后,我们添加XY平面的等高线:
ax.contourf(X,Y,Z,zdir='z',offset=-2,cmap=plt.get_cmap('rainbow'))
如果zdir选择了x,那么效果将会是对于XZ平面的投影。
因此,整个项目的代码为:
import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig=plt.figure() ax=Axes3D(fig) X=np.arange(-4,4,0.25) Y=np.arange(-4,4,0.25) X,Y=np.meshgrid(X,Y) R=np.sqrt(X ** 2 + Y ** 2) Z=np.sin(R) ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=plt.get_cmap('rainbow')) ax.contourf(X,Y,Z,zdir='z',offset=-2,cmap=plt.get_cmap('rainbow')) plt.show()
最终的效果图为:
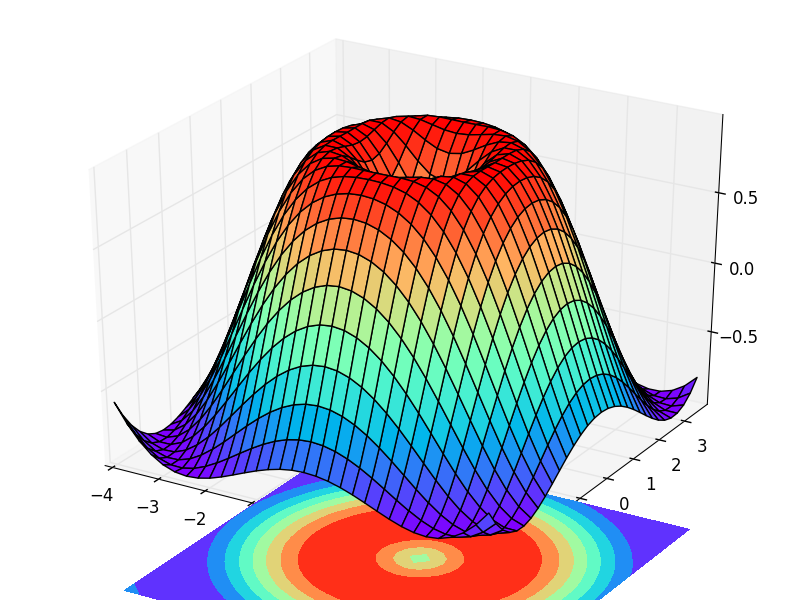
本知识学自于:莫烦python