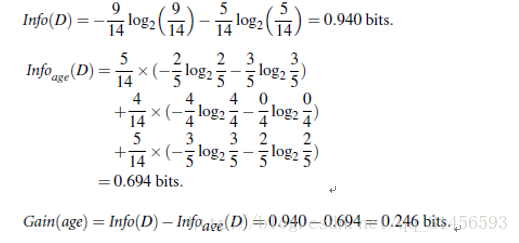机器学习算法及代码实现–决策树
1、决策树
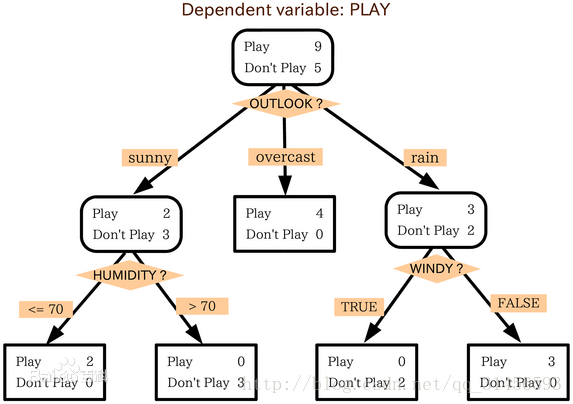
决策树算法的核心在于决策树的构建,每次选择让整体数据香农熵(描述数据的混乱程度)减小最多的特征,使用其特征值对数据进行划分,每次消耗一个特征,不断迭代分类,直到所有特征消耗完(选择剩下数据中出现次数最多的类别作为这堆数据的类别),或剩下的数据全为同一类别,不必继续划分,至此决策树构建完成,之后我们依照这颗决策树对新进数据进行分类。
2、信息熵
一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常非常不确定的事情,或者是我们一无所知的事情,需要了解大量信息==>信息量的度量就等于不确定性的多少
例子:猜世界杯冠军,假如一无所知,猜多少次?实际中每个队夺冠的几率不是相等的,如果我们对其有足够了解,是否猜中的概率会增大?
信息熵用比特(bit)来衡量信息的多少,变量的不确定性越大,熵也就越大。
公式:
3、决策树算法(ID3)
我们以一个例子来讲述决策树的算法(判断该用户是否买电脑)
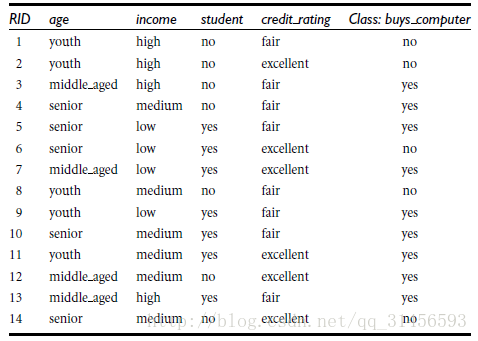
每次选择信息获取量最大的特征对其进行划分
Gain(A) = Info(D) - Infor_A(D) (原来的信息熵减去用A之后的信息熵=》获取的信息量)
计算过程:
类似,Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048
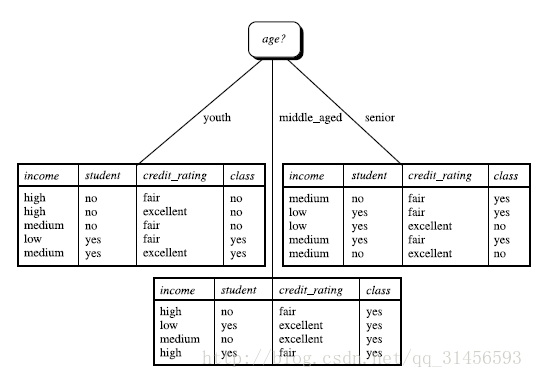
所以,选择age作为第一个根节点
分类结果:
算法注意点:
1)根节点开始,样本在同一个类则为树叶,标记类号
2)选择信息获取量最大的进行划分
3)属性为离散值连续则必须离散化
4)根据属性划分分支,分支的子节点不用再考虑该属性
停止条件
1)所有节点属于同一类
2)没有可划分的属性了: 以当中的大多数来确定类
3)属性下没节点:以父节点中的多少类作为类
4、其它决策树算法
C4.5、CART
5、对于过拟合的处理方法
先剪枝:一定深度不再分
后剪枝:先生成,后按规则减
6、优缺点
优点:直观、易理解、小规模数据有效
缺点:处理连续变量不好,值域不好划分
类别多时,错误增加快
可规模性一般,大量数据时复杂性大
算法实现
#-*- coding: utf-8 -*- from sklearn.feature_extraction import DictVectorizer import csv from sklearn import preprocessing from sklearn import tree from sklearn.externals.six import StringIO data = open('jueceshu.csv', 'rb') reader = csv.reader(data) headers = reader.next() print headers featureList = [] # 特征集 labelList = [] # 标签集 for row in reader: # 最后一列是标签,构造标签集 labelList.append(row[len(row)-1]) # 构造特征集 rowDict = {} for i in range(1, len(row)-1): # header里面是属性名,用来作键值 rowDict[headers[i]] = row[i] featureList.append(rowDict) print featureList vec = DictVectorizer() # 将特征转化为向量 dummyX = vec.fit_transform(featureList).toarray() print ('dummyX:'+str(dummyX)) # 输出向量中每一项的含义 print vec.get_feature_names() print 'labelList:' + str(labelList) # 将标签变成列向量 lb = preprocessing.LabelBinarizer() dummyY = lb.fit_transform(labelList) print 'dummyY:' + str(dummyY) # 利用tree中的分类器来创建决策树 clf = tree.DecisionTreeClassifier(criterion='entropy') # 用ID3的算法 信息熵 clf = clf.fit(dummyX, dummyY) print 'clf:' + str(clf) # 画决策树 with open('jueceshu.dot', 'w') as f: # 把feature_name返回 f = tree.export_graphviz(clf,feature_names=vec.get_feature_names(), out_file=f) oneRowX = dummyX[0, :] print 'oneRowX:' + str(oneRowX) # 构造新的情况,并预测 newRowX = oneRowX newRowX[0] = 1 newRowX[2] = 0 print 'newRowX:' + str(newRowX) # 用模型预测 predictedY = clf.predict(newRowX) print 'predictedY:' + str(predictedY)