https://vjudge.net/contest/214904
A
Kefa decided to make some money doing business on the Internet for exactly n days. He knows that on the i-th day (1 ≤ i ≤ n) he makes ai money. Kefa loves progress, that's why he wants to know the length of the maximum non-decreasing subsegment in sequence ai. Let us remind you that the subsegment of the sequence is its continuous fragment. A subsegment of numbers is called non-decreasing if all numbers in it follow in the non-decreasing order.
Help Kefa cope with this task!
Input
The first line contains integer n (1 ≤ n ≤ 105).
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109).
Output
Print a single integer — the length of the maximum non-decreasing subsegment of sequence a.
Example
6
2 2 1 3 4 1
3
3
2 2 9
3
Note
In the first test the maximum non-decreasing subsegment is the numbers from the third to the fifth one.
In the second test the maximum non-decreasing subsegment is the numbers from the first to the third one.
题意:求最长的非递减长度
思路:暴力
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<queue> #include<set> #include<algorithm> #include<map> #define maxn 200005 using namespace std; int main() { int a[maxn]; int m; cin>>m; for(int i=0;i<m;i++) { cin>>a[i]; } int ans=0; int maxx=0; for(int i=0;i<m;i++) { if(a[i]<=a[i+1])ans++; else if(a[i]>a[i+1]) { if(maxx<ans)maxx=ans; ans=0; } } cout<<maxx<<endl; return 0; }
B
Kefa wants to celebrate his first big salary by going to restaurant. However, he needs company.
Kefa has n friends, each friend will agree to go to the restaurant if Kefa asks. Each friend is characterized by the amount of money he has and the friendship factor in respect to Kefa. The parrot doesn't want any friend to feel poor compared to somebody else in the company (Kefa doesn't count). A friend feels poor if in the company there is someone who has at least d units of money more than he does. Also, Kefa wants the total friendship factor of the members of the company to be maximum. Help him invite an optimal company!
Input
The first line of the input contains two space-separated integers, n and d (1 ≤ n ≤ 105, ) — the number of Kefa's friends and the minimum difference between the amount of money in order to feel poor, respectively.
Next n lines contain the descriptions of Kefa's friends, the (i + 1)-th line contains the description of the i-th friend of type mi, si (0 ≤ mi, si ≤ 109) — the amount of money and the friendship factor, respectively.
Output
Print the maximum total friendship factir that can be reached.
Example
4 5
75 5
0 100
150 20
75 1
100
5 100
0 7
11 32
99 10
46 8
87 54
111
Note
In the first sample test the most profitable strategy is to form a company from only the second friend. At all other variants the total degree of friendship will be worse.
In the second sample test we can take all the friends.
题意:给你n个人m的差价
每个人有自己的价钱和带来的效益 公司到这n个人里选若干人,但是选取的每两个人之间差价不能超过m(不能等于)
求公司能获取的最大的效益
思路: 尺取法,,,简单题,,wa5次是因为:1,双循环超时 2,不能等于m 3,数据开long long
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<queue> #include<set> #include<algorithm> #include<map> #define maxn 100005 typedef long long ll; using namespace std; struct aa{ ll a; ll b; }; aa x[maxn]; bool cmp(aa zz,aa pp){ return zz.a<pp.a; } int main() { int n,d; ll sum[maxn]={0}; cin>>n>>d; for(int i=0;i<n;i++) { cin>>x[i].a>>x[i].b; } sort(x,x+n,cmp); for(int i=0;i<n;i++)sum[i]=sum[i-1]+x[i].b; int l=1; ll ans=0; for(ll r=0;r<n;++r) { while(l<n&&x[l].a-x[r].a<d)l++; ans=max(ans,sum[l-1]-sum[r-1]); } cout<<ans<<endl; return 0; }
C
Kefa decided to celebrate his first big salary by going to the restaurant.
He lives by an unusual park. The park is a rooted tree consisting of n vertices with the root at vertex 1. Vertex 1 also contains Kefa's house. Unfortunaely for our hero, the park also contains cats. Kefa has already found out what are the vertices with cats in them.
The leaf vertices of the park contain restaurants. Kefa wants to choose a restaurant where he will go, but unfortunately he is very afraid of cats, so there is no way he will go to the restaurant if the path from the restaurant to his house contains more than m consecutive vertices with cats.
Your task is to help Kefa count the number of restaurants where he can go.
Input
The first line contains two integers, n and m (2 ≤ n ≤ 105, 1 ≤ m ≤ n) — the number of vertices of the tree and the maximum number of consecutive vertices with cats that is still ok for Kefa.
The second line contains n integers a1, a2, ..., an, where each ai either equals to 0 (then vertex i has no cat), or equals to 1 (then vertex i has a cat).
Next n - 1 lines contains the edges of the tree in the format "xi yi" (without the quotes) (1 ≤ xi, yi ≤ n, xi ≠ yi), where xi and yi are the vertices of the tree, connected by an edge.
It is guaranteed that the given set of edges specifies a tree.
Output
A single integer — the number of distinct leaves of a tree the path to which from Kefa's home contains at most m consecutive vertices with cats.
Example
4 1
1 1 0 0
1 2
1 3
1 4
2
7 1
1 0 1 1 0 0 0
1 2
1 3
2 4
2 5
3 6
3 7
2
Note
Let us remind you that a tree is a connected graph on n vertices and n - 1 edge. A rooted tree is a tree with a special vertex called root. In a rooted tree among any two vertices connected by an edge, one vertex is a parent (the one closer to the root), and the other one is a child. A vertex is called a leaf, if it has no children.
Note to the first sample test: The vertices containing cats are marked red. The restaurants are at vertices 2, 3, 4. Kefa can't go only to the restaurant located at vertex 2.
Note to the second sample test: The restaurants are located at vertices 4, 5, 6, 7. Kefa can't go to restaurants 6, 7.
题意:A的家在1,其余没有子节点的点都是餐厅,途中不能经过m次以上的红点(值为1)问他能去几个餐厅?
思路:深搜。需要注意的是他是无向的。(链式前向性)
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<queue> #include<set> #include<algorithm> #include<map> #define maxn 100005 using namespace std; vector<int>mp[maxn]; bool vis[maxn]; int dis[maxn]; int n,m; int a,b; int ans=0; int dfs(int res,int ans) { if(dis[res])ans++; else ans=0; if(ans>m||vis[res])return 0; vis[res]=true; int flag=0; if(res>1&&mp[res].size()==1)return 1; for(int i=0;i<mp[res].size();i++){ flag=flag+dfs(mp[res][i],ans); } return flag; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { cin>>dis[i]; } for(int i=0;i<n-1;i++) { cin>>a>>b; mp[a].push_back(b); mp[b].push_back(a); } for(int i=0;i<=n;i++) vis[i]=false; int zz=dfs(1,0); cout<<zz<<endl; return 0; }
D
Polycarp loves geometric progressions very much. Since he was only three years old, he loves only the progressions of length three. He also has a favorite integer k and a sequence a, consisting of n integers.
He wants to know how many subsequences of length three can be selected from a, so that they form a geometric progression with common ratio k.
A subsequence of length three is a combination of three such indexes i1, i2, i3, that 1 ≤ i1 < i2 < i3 ≤ n. That is, a subsequence of length three are such groups of three elements that are not necessarily consecutive in the sequence, but their indexes are strictly increasing.
A geometric progression with common ratio k is a sequence of numbers of the form b·k0, b·k1, ..., b·kr - 1.
Polycarp is only three years old, so he can not calculate this number himself. Help him to do it.
Input
The first line of the input contains two integers, n and k (1 ≤ n, k ≤ 2·105), showing how many numbers Polycarp's sequence has and his favorite number.
The second line contains n integers a1, a2, ..., an ( - 109 ≤ ai ≤ 109) — elements of the sequence.
Output
Output a single number — the number of ways to choose a subsequence of length three, such that it forms a geometric progression with a common ratio k.
Example
5 2
1 1 2 2 4
4
3 1
1 1 1
1
10 3
1 2 6 2 3 6 9 18 3 9
6
Note
In the first sample test the answer is four, as any of the two 1s can be chosen as the first element, the second element can be any of the 2s, and the third element of the subsequence must be equal to 4.
题意:给定n个数和k的倍数
在n个数组找任意三个数组成等比数列 (只能按顺序组成) 比如第二个样例: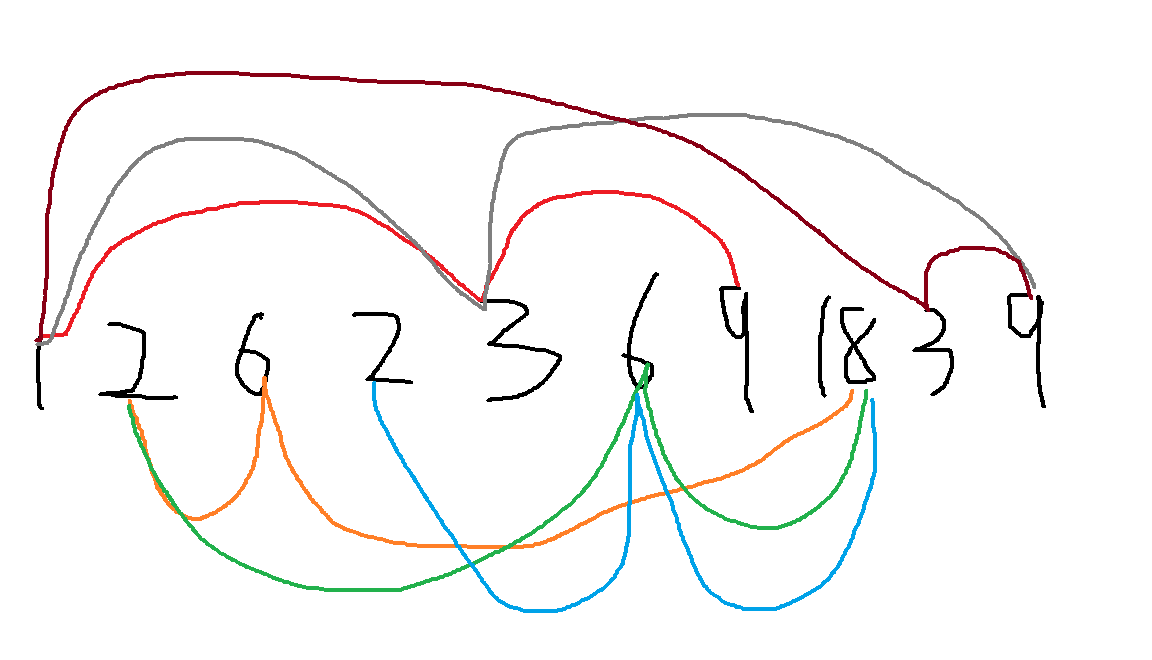
求最多能组成多少组等比数列
思路: map存储,,dp思想,,
定义:dp[i][j] 以j结尾的长度为i的子序列的个数
有转移方程
注意这里的数j/kj/k必须位于数列中j之前的位置,所以这里实现的时候运用了一个边转移边添加元素的方法,非常经典,且由于树的大小为109109这里用了map数组来离散化查找,详细见代码
代码:
#include <bits/stdc++.h> using namespace std; typedef long long LL; map<int, LL> dp[4]; int n, k, v[200000+100]; int main(void) { cin >> n >> k; for (int i = 0; i < n; i++) scanf("%d", &v[i]); LL ans = 0; for (int j = 0; j < n; j++) { int x = v[j]; if (x % k == 0) { ans += dp[2][x / k]; dp[2][x] += dp[1][x / k]; } dp[1][x] += 1; } cout << ans << endl; return 0; }
其实两个map也一样的
//#include<iostream>
//#include<cstdio>
//#include<cstring>
//#include<cmath>
//#include<queue>
//#include<set>
//#include<algorithm>
//#include<map>
//#define maxn 200005
//typedef long long ll;
//using namespace std;
//map<int,ll>s1;
//map<int,ll>s2;
//int main()
//{
// int m,k;
// ll ans,x;
// cin>>m>>k;
// ans=0;
// for(int i=0;i<m;i++)
// {
// cin>>x;
// if(x%k==0){
// ans+=s2[x/k];
// s2[x]+=s1[x/k];
// }
// s1[x]++;
// }
// cout<<ans<<endl;
//}
这题在网上看的一种离散化+二分搜索优化的代码(代码贼复杂),,本来打算补的,突然发现dp更简单而且理解就只粘了dp的code