概论
PriorityQueue 类在 Java1.5 中引入并作为 Java Collections Framework 的一部分。PriorityQueue 是基于优先堆的一个无界队列,这个优先队列中的元素可以默认自然排序或者通过提供的 Comparator(比较器)在队列实例化的时排序。
优先队列不允许空值,而且不支持 non-comparable(不可比较)的对象,比如用户自定义的类。优先队列要求使用 Java Comparable 和 Comparator 接口给对象排序,并且在排序时会按照优先级处理其中的元素。如果你插入一个non-comparable对象,则会抛出一个 ClassCastException 异常。
优先队列的头是基于自然排序或者 Comparator 排序的最小元素。如果有多个对象拥有同样的排序,那么就可能随机地取其中任意一个。当我们获取队列时,返回队列的头对象。
优先队列的大小是不受限制的,但在创建时可以指定初始大小。它内部的有一个 “capacity” 管理着数组的大小,该数组用于存储队列的元素。它总是至少同队列大小一样大。当我们向优先队列增加元素的时候,队列大小会自动增加。并没有指定增长策略的细节。
该类和它的迭代器实现了 Collection 和 Iterator 接口所有可选的方法。迭代器提供的 iterator() 方法不保证遍历优先级队列的元素根据任何特别的顺序。如果你需要有序的遍历,考虑使用 Arrays.sort(pq.toArray()).
PriorityQueue 是非线程安全的,所以 Java 提供了 PriorityBlockingQueue(实现 BlockingQueue 接口)用于 Java 多线程环境。
实现注意:该实现提供了 O(log(n)) 时间复杂度对于入队和出队方法:offer、poll、remove() 和 add;线性的时间 O(n) 对于 remove(object) 和 contains(object) 方法;和常量的时间O(1)对于检索方法:peek、element 和 size。
数据结构
二叉堆是一种特殊的堆,二叉堆是完全二叉树或者是近似完全二叉树。二叉堆有两种:最大堆和最小堆。最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。
Priority queue 是一个 平衡二叉堆(平衡二叉树);树中所有的子节点必须大于等于父节点,而无需维护大小关系,是一个最小堆。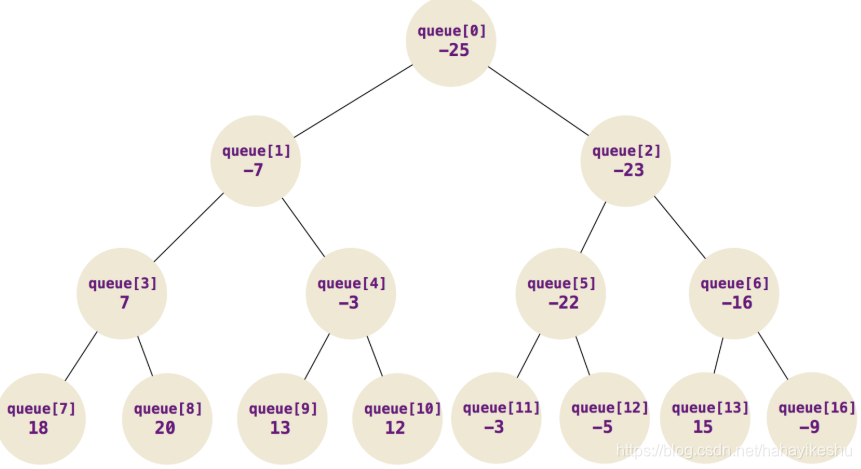
- 父节点与子节点的索引关系:
-
假设父节点为 queue[n],那么左孩子节点为 queue[2n+1],右孩子节点为 queue[2(n+1)]
-
假设孩子节点(无论是左孩子节点还是右孩子节点)为 queue[n],n>0。那么父节点为 queue[(n-1) >>> 1]
节点间的大小关系:
-
父节点总是小于等于孩子节点
-
同一层孩子节点间的大小无需维护
- 叶子节点和非叶子节点:
- 一个长度为 size 的优先级队列,当 index >= size >>> 1 时,该节点为叶子节点。否则,为非叶子节点
PriorityQueue 的源码分析
基本属性
先来看下 PriorityQueue 的定义
public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
可以看到 PriorityQueue 继承了 AbstractQueue 抽象类,并实现了 Serializable 接口,AbstractQueue 抽象类实现了 Queue 接口,对其中方法进行了一些通用的封装,具体就不多看了。
下面看看里面定义的一些属性:
// 默认初始化大小
private static final int DEFAULT_INITIAL_CAPACITY = 11; /** * Priority queue represented as a balanced binary heap: the two * children of queue[n] are queue[2*n+1] and queue[2*(n+1)]. The * priority queue is ordered by comparator, or by the elements' * natural ordering, if comparator is null: For each node n in the * heap and each descendant d of n, n <= d. The element with the * lowest value is in queue[0], assuming the queue is nonempty. 数组来实现的队列,是 Object 类型,兼容任何对象。 */ transient Object[] queue; // non-private to simplify nested class access /** * The number of elements in the priority queue. 当前容量 */ int size; /** * The comparator, or null if priority queue uses elements' 比较器 * natural ordering. */ private final Comparator<? super E> comparator; /** * The number of times this priority queue has been * <i>structurally modified</i>. See AbstractList for gory details. 记录修改次数 */ transient int modCount; // non-private to simplify nested class access
/** * The maximum size of array to allocate. * Some VMs reserve some header words in an array. * Attempts to allocate larger arrays may result in * OutOfMemoryError: Requested array size exceeds VM limit */ private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
最大容量 -8 是因为一些虚拟机会有些头字母保存在数组中,此外创造大容量的数组容易导致 OOM(数组容量超过虚拟机的限制)。
构造方法
/** * 不带参数的构造函数,最终会给一个默认值*/ public PriorityQueue() { this(DEFAULT_INITIAL_CAPACITY, null); } /** * 用户可以自己定义初始大小
* 小于1会抛出错误*/ public PriorityQueue(int initialCapacity) { this(initialCapacity, null); } /** * 传入一个比较器,队列初始大小是默认大小,如果传入的比较器为null,就会使用自然排序 * @since 1.8 */ public PriorityQueue(Comparator<? super E> comparator) { this(DEFAULT_INITIAL_CAPACITY, comparator); } /** * 可以设置初始容量和比较器,注意给定的初始大小不能小于1*/ public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) { // Note: This restriction of at least one is not actually needed, // but continues for 1.5 compatibility if (initialCapacity < 1) throw new IllegalArgumentException(); this.queue = new Object[initialCapacity]; this.comparator = comparator; } /** * 根据传入的集合创建一个优先级队列,如果传入的集合属于 SortedSet 或者本身是一个优先级队列,那么还是按照原来的排序规则进行排序,否则就是按照自然排序 * 注意如果集合中存在 null 元素,会抛出NPE异常*/ @SuppressWarnings("unchecked") public PriorityQueue(Collection<? extends E> c) { if (c instanceof SortedSet<?>) { SortedSet<? extends E> ss = (SortedSet<? extends E>) c; this.comparator = (Comparator<? super E>) ss.comparator(); initElementsFromCollection(ss); } else if (c instanceof PriorityQueue<?>) { PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c; this.comparator = (Comparator<? super E>) pq.comparator(); initFromPriorityQueue(pq); } else { this.comparator = null; initFromCollection(c); } } /** * 根据传入的优先级队列创造一个队列,排序规则和原来保持一样
* 同样注意 null 元素引起的 NPE 问题 */ @SuppressWarnings("unchecked") public PriorityQueue(PriorityQueue<? extends E> c) { this.comparator = (Comparator<? super E>) c.comparator(); initFromPriorityQueue(c); } /** * 根据 SortedSet 集合来创建优先级队列*/ @SuppressWarnings("unchecked") public PriorityQueue(SortedSet<? extends E> c) { this.comparator = (Comparator<? super E>) c.comparator(); initElementsFromCollection(c); }
// 如果是优先级队列,直接调用 toArray 方法转成数组(内部使用Arrays.copy实现),获取其容量大小。
// 不是优先级队列就会调用根据集合来进行初始化 private void initFromPriorityQueue(PriorityQueue<? extends E> c) { if (c.getClass() == PriorityQueue.class) { this.queue = c.toArray(); this.size = c.size(); } else { initFromCollection(c); } }
// 对于集合的初始化 private void initElementsFromCollection(Collection<? extends E> c) { Object[] a = c.toArray(); // If c.toArray incorrectly doesn't return Object[], copy it. if (a.getClass() != Object[].class)
// 将其变成 Object 类型 a = Arrays.copyOf(a, a.length, Object[].class); int len = a.length; if (len == 1 || this.comparator != null) for (Object e : a)
// 判断是否存在为null的元素 if (e == null) throw new NullPointerException(); this.queue = a; this.size = a.length; } /** * Initializes queue array with elements from the given Collection. * * @param c the collection */ private void initFromCollection(Collection<? extends E> c) { initElementsFromCollection(c);
// 调用该方法给队列进行调整,形成二叉堆 heapify(); }
可以发现其构造方法还是很多的,考虑到了各种不同的情况,同时也给了一些默认值。使用者可以根据使用场景,来进行初始化。
入队原理
二叉堆(最小堆为例)的特点:
-
父结点的键值总是小于或等于任何一个子节点的键值。
-
基于数组实现的二叉堆,对于数组中任意位置的n上元素,其左孩子在[2n+1]位置上,右孩子[2(n+1)]位置,它的父亲则在[n-1/2]上,而根的位置则是[0]。
为了维护这个特点,二叉堆在添加元素的时候,需要一个"上移"的动作,什么是"上移"呢,我们继续用图来说明。
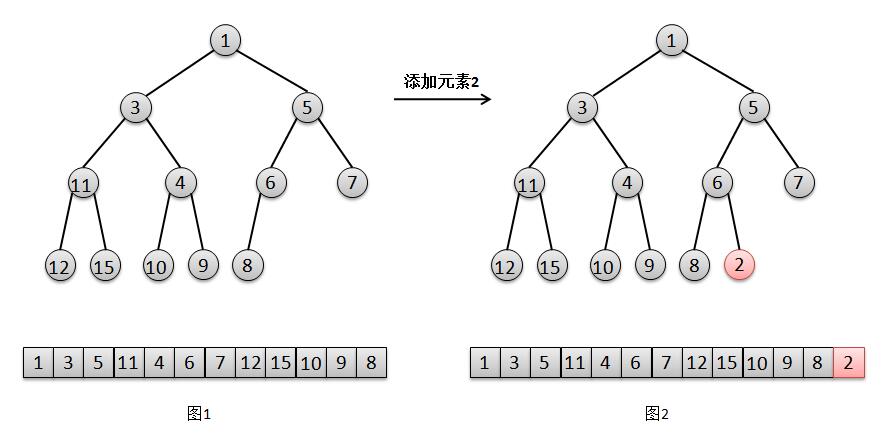
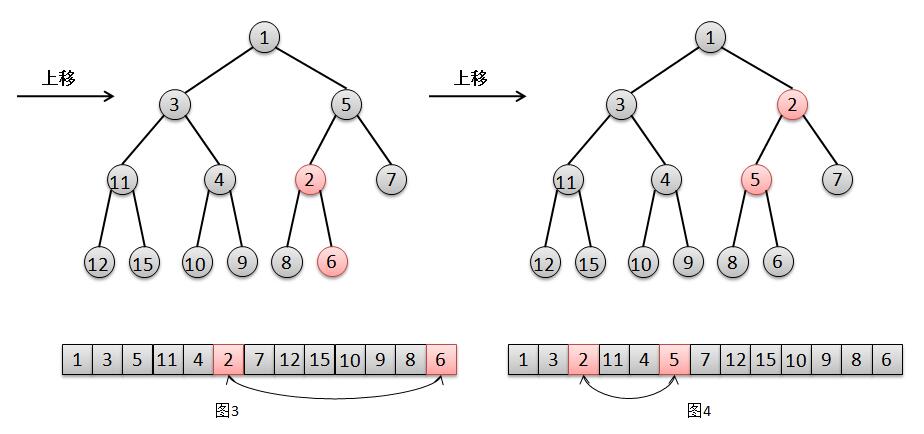
结合上面的图解,我们来说明一下二叉堆的添加元素过程:
-
将元素2添加在最后一个位置(队尾)(图2)。
-
由于2比其父亲6要小,所以将元素2上移,交换2和6的位置(图3);
-
然后由于2比5小,继续将2上移,交换2和5的位置(图4),此时2大于其父亲(根节点)1,结束。
看完了这 4 张图,是不是觉得二叉堆的添加还是挺容易的,那么下面我们具体看下 PriorityQueue 的代码是怎么实现入队操作的吧。
/** * 插入一个元素,返回 true 代表添加成功*/ public boolean add(E e) { return offer(e); } /** * 插入一个元素到队列中去*/ public boolean offer(E e) { if (e == null) throw new NullPointerException();
// 每次添加,意味着依次修改 modCount++; int i = size; // size是记录当前元素个数的,并不是根据 queue.length,因为存在未添加的情况
// 如果 size 大于等于队列的长度,就说明应该扩容了 if (i >= queue.length) grow(i + 1); size = i + 1; if (i == 0) queue[0] = e; else siftUp(i, e); // 添加到队尾,进行上移判断 return true; }
/** * Increases the capacity of the array. * * @param minCapacity the desired minimum capacity */ private void grow(int minCapacity) { int oldCapacity = queue.length; // Double size if small; else grow by 50% int newCapacity = oldCapacity + ((oldCapacity < 64) ? (oldCapacity + 2) : (oldCapacity >> 1)); // overflow-conscious code 判断是否超过最大容量 if (newCapacity - MAX_ARRAY_SIZE > 0) newCapacity = hugeCapacity(minCapacity); queue = Arrays.copyOf(queue, newCapacity); }
根据上面的方法实现,其扩容规则是这样的,当队列长度小于 64 的时候,基本上就是扩容一倍;但是当队列长度大于 64 之后,就会扩容 50%。扩容完成后,还要对新的容量进行判断是否符合要求,否则还是需要进一步调整的。然后再把队列的元素赋值到新的数组中。
private static int hugeCapacity(int minCapacity) { if (minCapacity < 0) // overflow throw new OutOfMemoryError(); return (minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE; }
需要理解的是,这里为什么当 minCapacity 小于 0 的时候,就代表超出 int 范围呢,我们来看下。
int 在java中占 4 个字节,一个字节 8 位,从 0 开始记,那么 4 个字节的最高位就是31,而 java 中的基本数据类型都是有符号的,所以最高位代表的是符号位。
int 的最大值 Integer.MAX_VALUE = 0111 1111 1111 1111 1111 1111 1111 1111,Integer.MAX_VALUE+1 = 1000 0000 0000 0000 0000 0000 0000 0000,此时最高位是符号位为 1,所以这个数是负数。负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后 +1(即在反码的基础上 +1)。容量超了之后就会抛出 OOM。
接下去就是要看看元素是如何移动的。
/**
* 指定位置 K 插入元素 x,为了保持堆的结构,需要确保其插入后大于等于父节点。根据有没有比较器,分成了两个方法,加快速度 */ private void siftUp(int k, E x) { if (comparator != null) siftUpUsingComparator(k, x); else siftUpComparable(k, x); } @SuppressWarnings("unchecked") private void siftUpComparable(int k, E x) {
// 实现了 Comparable 接口,进行强转,便于比较,如果没有实现,就会抛出强转错误 Comparable<? super E> key = (Comparable<? super E>) x; while (k > 0) { int parent = (k - 1) >>> 1; Object e = queue[parent]; if (key.compareTo((E) e) >= 0) break; queue[k] = e; k = parent; } queue[k] = key; } @SuppressWarnings("unchecked") private void siftUpUsingComparator(int k, E x) { while (k > 0) {
// 获取父节点 int parent = (k - 1) >>> 1; Object e = queue[parent];
// 当前位置满足条件的话,就会跳出循环 if (comparator.compare(x, (E) e) >= 0) break;
// 交换位置,把父节点移到位置K处 queue[k] = e; k = parent; } queue[k] = x; }
到这里,上移过程就结束了,可以发现整个上移过程还是比较简单的,起主要逻辑就是获取父节点,然后进行比较,要不要交换位置。插入操作的时间复杂度为 O(log(n));
出队原理
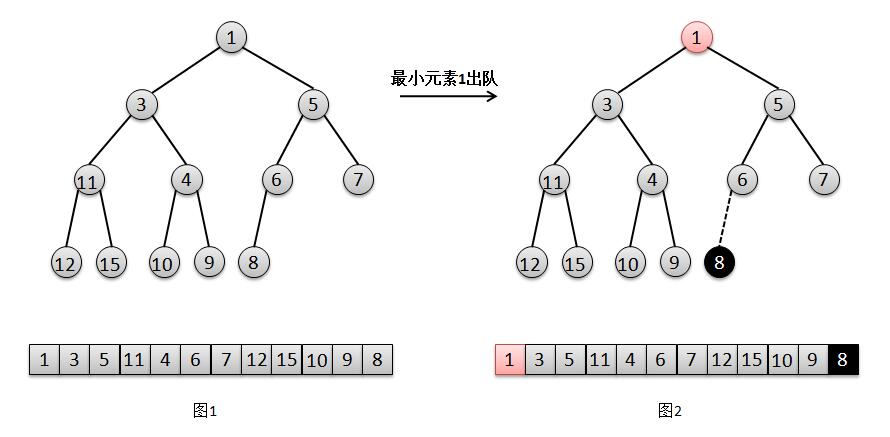

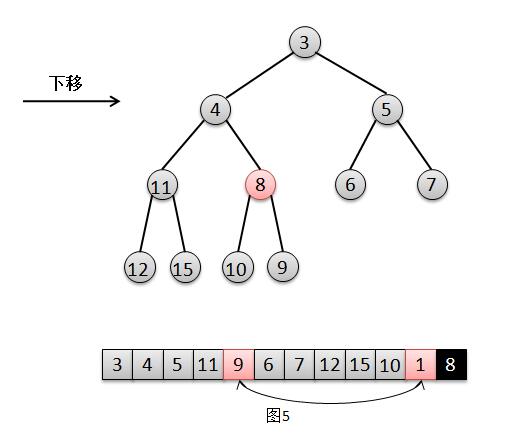
结合上面的图解,我们来说明一下二叉堆的出队过程:
-
将找出队尾的元素 8,并将它在队尾位置上删除(图2);
-
此时队尾元素 8 比根元素 1 的最小孩子 3 要大,所以将元素 1 下移,交换 1 和 3 的位置(图3);
-
然后此时队尾元素 8 比元素 1 的最小孩子 4 要大,继续将 1 下移,交换 1 和 4 的位置(图4);
-
然后此时根元素 8 比元素 1 的最小孩子 9 要小,不需要下移,直接将根元素 8 赋值给此时元素 1 的位置,1被覆盖则相当于删除(图5),结束。
看完了这 6 张图,下面我们具体看下 PriorityQueue 的代码是怎么实现出队操作的吧。
/** * 移除一个元素,如果存在的话*/ public boolean remove(Object o) { int i = indexOf(o); if (i == -1) return false; else { removeAt(i); return true; } } /** * 迭代的时候进行移除*/ boolean removeEq(Object o) { for (int i = 0; i < size; i++) { if (o == queue[i]) { removeAt(i); return true; } } return false; } /** * 移除第 i 个位置的元素 */ @SuppressWarnings("unchecked") E removeAt(int i) { // assert i >= 0 && i < size; 增加修改次数 modCount++; int s = --size; if (s == i) // removed last element ,如果是最后一位直接置null,表示删除 queue[i] = null; else { E moved = (E) queue[s]; // 获取最后一位元素 queue[s] = null; siftDown(i, moved); // 第 i 位元素下移,同时最后一位元素要上移
// 相等,说明此时删除的是叶子节点,这时候需要看看要不要上升 if (queue[i] == moved) { siftUp(i, moved); // 最后一个元素需要上升 if (queue[i] != moved) return moved; } } return null; }
/**
* 在位置 k 处插入元素 x,同时为了保证堆的不变性,需要对 x 的向下移动,直到其子节点都大于它 */ private void siftDown(int k, E x) {
// 这里根据比较器是否为空来选择不同的方法 if (comparator != null) siftDownUsingComparator(k, x); else siftDownComparable(k, x); } @SuppressWarnings("unchecked") private void siftDownComparable(int k, E x) { Comparable<? super E> key = (Comparable<? super E>)x;
// 先找到中间节点 int half = size >>> 1; // loop while a non-leaf while (k < half) {
// 找到其左子节点 int child = (k << 1) + 1; // assume left child is least Object c = queue[child]; int right = child + 1; if (right < size && ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0) // compare 返回 -1,0,1说明 o1 < o2, o1=o2, o1>o2
// 取其中较小的子节点 c = queue[child = right];
// 比较插入的节点是否比子节点小,如果小,说明插入位置合适 if (key.compareTo((E) c) <= 0) break;
// 否则就和较小的子节点交换位置,继续循环 queue[k] = c; k = child; } queue[k] = key; } @SuppressWarnings("unchecked") private void siftDownUsingComparator(int k, E x) { int half = size >>> 1; while (k < half) { int child = (k << 1) + 1; Object c = queue[child]; int right = child + 1; if (right < size && comparator.compare((E) c, (E) queue[right]) > 0) c = queue[child = right];
// 找到退出循环 if (comparator.compare(x, (E) c) <= 0) break; queue[k] = c; k = child; } queue[k] = x; }
jdk 中,不是直接将根元素删除,然后再将下面的元素做上移,重新补充根元素;而是找出队尾的元素,并在队尾的位置上删除,然后通过根元素的下移,给队尾元素找到一个合适的位置,最终覆盖掉跟元素,从而达到删除根元素的目的。这样做在一些情况下,会比直接删除在上移根元素,或者直接下移根元素再调整队尾元素的位置少操作一些步奏(比如上面图解中的例子,不信你可以试一下^_^)。
明白了二叉堆的入队和出队操作后,其他的方法就都比较简单了,下面我们再来看一个二叉堆中比较重要的过程,二叉堆的构造。
堆的构造
/** * Establishes the heap invariant (described above) in the entire tree, * assuming nothing about the order of the elements prior to the call. */ @SuppressWarnings("unchecked") private void heapify() { for (int i = (size >>> 1) - 1; i >= 0; i--) siftDown(i, (E) queue[i]); }
这个方法很简单,就这几行代码,但是理解起来却不是那么容器的,我们来分析下。
假设有一个无序的数组,要求我们将这个数组建成一个二叉堆,你会怎么做呢?最简单的办法当然是将数组的数据一个个取出来,调用入队方法。但是这样做,每次入队都有可能会伴随着元素的移动,这么做是十分低效的。那么有没有更加高效的方法呢,我们来看下。
为了方便,我们将上面我们图解中的数组去掉几个元素,只留下7、6、5、12、10、3、1、11、15、4(顺序已经随机打乱)。ok、那么接下来,我们就按照当前的顺序建立一个二叉堆,暂时不用管它是否符合标准。
int a = [7, 6, 5, 12, 10, 3, 1, 11, 15, 4 ];
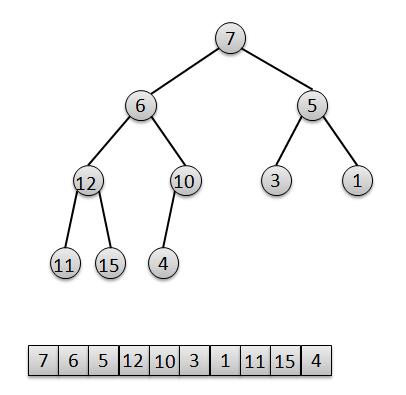
我们观察下用 数组a 建成的二叉堆,很明显,对于叶子节点 4、15、11、1、3 来说,它们已经是一个合法的堆。所以只要最后一个节点的父节点,也就是最后一个非叶子节点 a[4]=10 开始调整,然后依次调整 a[3]=12,a[2]=5,a[1]=6,a[0]=7,分别对这几个节点做一次"下移"操作就可以完成了堆的构造。ok,我们还是用图解来分析下这个过程。
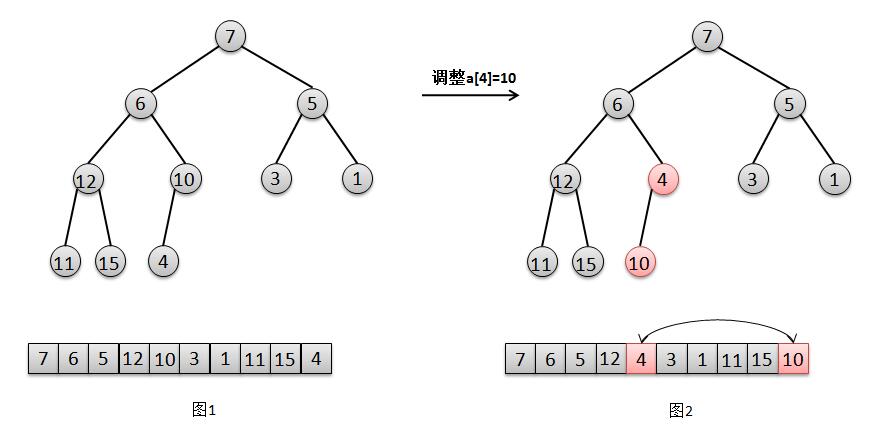
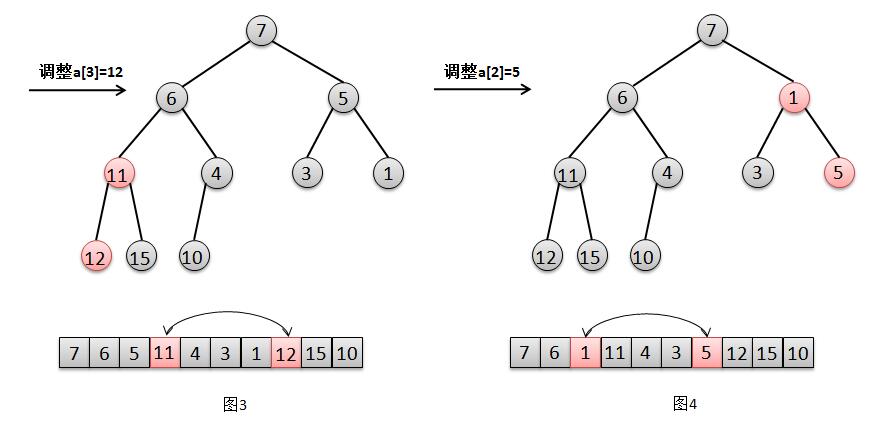

我们参照图解分别来解释下这几个步奏:
-
对于节点 a[4]=10 的调整(图1),只需要交换元素 10 和其子节点 4 的位置(图2)。
-
对于节点 a[3]=12 的调整,只需要交换元素 12 和其最小子节点 11 的位置(图3)。
-
对于节点 a[2]=5 的调整,只需要交换元素 5 和其最小子节点 1 的位置(图4)。
-
对于节点 a[1]=6 的调整,只需要交换元素 6 和其最小子节点 4 的位置(图5)。
-
对于节点 a[0]=7 的调整,只需要交换元素 7 和其最小子节点 1 的位置,然后交换 7 和其最小自己点 3 的位置(图6)。
至此,调整完毕,建堆完成。
1 private void heapify() {
2 for (int i = (size >>> 1) - 1; i >= 0; i--)
3 siftDown(i, (E) queue[i]);
4 }
int i = (size >>> 1) - 1,这行代码是为了找寻最后一个非叶子节点,然后倒序进行"下移" siftDown 操作,是不是很显然了。
其他
清除优先级队列中所有节点
/** * Removes all of the elements from this priority queue. * The queue will be empty after this call returns. */ public void clear() { modCount++; for (int i = 0; i < size; i++) queue[i] = null; size = 0; }
清除优先级队列中的所有节点。该操作的事件复杂度为:O(n);
迭代器
优先级队列的迭代器并不保证遍历按照指定的顺序获取节点元素。这是因为当在迭代器中执行 remove 操作时,可能会涉及到一个未访问的元素被移动到了一个已经访问过的节点位置(删除操作时,当队尾节点被放置到待移除节点位置的情况下,需要调用 siftUp 方法,siftUp(index, object) 方法会升高待插入元素在树中的位置 index,直到待插入的元素大于或等于它待插入位置的父节点)。在迭代器操作中需要特殊处理。此时这些不幸的元素会在所有节点遍历完后才得以遍历。
@SuppressWarnings("unchecked")
public E next() {
if (expectedModCount != modCount)
throw new ConcurrentModificationException();
// 说明有元素被删除了
if (cursor < size)
return (E) queue[lastRet = cursor++];
if (forgetMeNot != null) {
lastRet = -1;
lastRetElt = forgetMeNot.poll();
// 被移动的元素最后
if (lastRetElt != null)
return lastRetElt;
}
throw new NoSuchElementException();
}
// 在迭代器中删除元素的时候,此时删除的位置是已经访问过的,此时很可能把一个未被访问的元素放到该位置,导致被移动的元素没有被访问到,需要记录下来
public void remove() {
// 修改次数不一致,就会抛出错误
if (expectedModCount != modCount)
throw new ConcurrentModificationException();
// 记录要删除的元素
if (lastRet != -1) {
` // 此处返回的是被移动元素,而不是被删除的元素
E moved = PriorityQueue.this.removeAt(lastRet);
lastRet = -1;
// 说明对列已经没有该元素
if (moved == null)
cursor--;
else {
if (forgetMeNot == null)
forgetMeNot = new ArrayDeque<>();
// 移动元素加入到遗忘队列,之所以这么操作是因为移动元素很可能被放到已经访问过的地方,因此需要在次被访问到。
forgetMeNot.add(moved);
}
} else if (lastRetElt != null) {
PriorityQueue.this.removeEq(lastRetElt);
lastRetElt = null;
} else {
throw new IllegalStateException();
}
// 更新修改次数
expectedModCount = modCount;
}
到这里 PriorityQueue 的基本操作就分析完了,明白了其底层二叉堆的概念及其入队、出队、建堆等操作,其他的一些方法代码就很简单了,这里就不一一分析了。