数据结构——二叉树的知识点总结

 树的遍历：

1、前序遍历    

前序遍历（DLR，lchild,data,rchild），是二叉树遍历的一种，也叫做先根遍历、先序遍历、前序周游，可记做根左右。前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。

前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。
若二叉树为空则结束返回，否则：

• 访问根结点。

• 前序遍历左子树。

• 前序遍历右子树 。

需要注意的是：遍历左右子树时仍然采用前序遍历方法。
如图所示二叉树

 

前序遍历结果：ABDECF

已知后序遍历和中序遍历，就能确定前序遍历。

其实在遍历二叉树的时候有三次遍历， 比如：

前序遍历：A->B->D->D(D左子节点并返回到D)->D(D右子节点并返回到D)->B->E->E(左)->E(右)->->B->A->C->F->F(左)->F(右)->C->C(右)，所以可以用栈结构，把遍历到的节点压进栈，没子节点时再出栈。也可以用递归的方式，递归的输出当前节点，然后递归的输出左子节点，最后递归的输出右子节点。直接看代码更能理解：

import java.util.Stack;
//前序遍历的递归实现与非递归实现
public class Test {
    public static void main(String[] args) {
        // 以数组形式生成一棵完全二叉树
        TreeNode[] node = new TreeNode[10];
        for (int i = 0; i < 10; i++) {
            node[i] = new TreeNode(i);
        }
        for (int i = 0; i < 10; i++) {
            if (i * 2 + 1 < 10)
                node[i].left = node[i * 2 + 1];
            if (i * 2 + 2 < 10)
                node[i].right = node[i * 2 + 2];
        }

        preOrderRe(node[0]);
    }
    // 递归实现
    public static void preOrderRe(TreeNode biTree) {
        System.out.println(biTree.value);
        TreeNode leftTree = biTree.left;
        if (leftTree != null) {
            preOrderRe(leftTree);
        }
        TreeNode rightTree = biTree.right;
        if (rightTree != null) {
            preOrderRe(rightTree);
        }
    }
    // 非递归实现
    public static void preOrder(TreeNode biTree) {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while (biTree != null || !stack.isEmpty()) {
            while (biTree != null) {
                System.out.println(biTree.value);
                stack.push(biTree);
                biTree = biTree.left;
            }
            if (!stack.isEmpty()) {
                biTree = stack.pop();
                biTree = biTree.right;
            }
        }
    }
}
// 节点结构
class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;

    TreeNode(int value) {
        this.value = value;
    }
}

2.中序遍历

中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，先左后根再右。巧记：左根右。中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。若二叉树为空则结束返回，否则：

• 中序遍历左子树
• 访问根结点
• 中序遍历右子树

如图所示二叉树

中序遍历结果：DBEAFC

public class Test {
    public static void main(String[] args) {
        // 以数组形式生成一棵完全二叉树
        TreeNode[] node = new TreeNode[10];
        for (int i = 0; i < 10; i++) {
            node[i] = new TreeNode(i);
        }
        for (int i = 0; i < 10; i++) {
            if (i * 2 + 1 < 10)
                node[i].left = node[i * 2 + 1];
            if (i * 2 + 2 < 10)
                node[i].right = node[i * 2 + 2];
        }

        midOrderRe(node[0]);
        System.out.println();
        midOrder(node[0]);
    }
    
    // 中序遍历递归实现
    public static void midOrderRe(TreeNode biTree) {
        if (biTree == null)
            return;
        else {
            midOrderRe(biTree.left);
            System.out.println(biTree.value);
            midOrderRe(biTree.right);
        }
    }

    // 中序遍历费递归实现
    public static void midOrder(TreeNode biTree) {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while (biTree != null || !stack.isEmpty()) {
            while (biTree != null) {
                stack.push(biTree);
                biTree = biTree.left;
            }
            if (!stack.isEmpty()) {
                biTree = stack.pop();
                System.out.println(biTree.value);
                biTree = biTree.right;
            }
        }
    }
}

//节点结构
class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;

    TreeNode(int value) {
        this.value = value;
    }
}

3、后序遍历（难点）

后序遍历（LRD）是二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中，先左后右再根。巧记：左右根。

后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。即：
若二叉树为空则结束返回，

否则：

• 后序遍历左子树

• 后序遍历右子树

• 访问根结点

如图所示二叉树

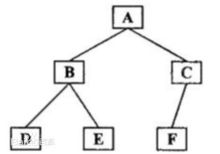
后序遍历结果：DEBFCA

已知前序遍历和中序遍历，就能确定后序遍历。

算法核心思想：

首先要搞清楚先序、中序、后序的非递归算法共同之处：用栈来保存先前走过的路径，以便可以在访问完子树后,可以利用栈中的信息,回退到当前节点的双亲节点,进行下一步操作。

后序遍历的非递归算法是三种顺序中最复杂的，原因在于，后序遍历是先访问左、右子树,再访问根节点，而在非递归算法中，利用栈回退到时，并不知道是从左子树回退到根节点，还是从右子树回退到根节点，如果从左子树回退到根节点，此时就应该去访问右子树，而如果从右子树回退到根节点，此时就应该访问根节点。所以相比前序和后序，必须得在压栈时添加信息，以便在退栈时可以知道是从左子树返回，还是从右子树返回进而决定下一步的操作。

public class Test {
    public static void main(String[] args) {
        // 以数组形式生成一棵完全二叉树
        TreeNode[] node = new TreeNode[10];
        for (int i = 0; i < 10; i++) {
            node[i] = new TreeNode(i);
        }
        for (int i = 0; i < 10; i++) {
            if (i * 2 + 1 < 10)
                node[i].left = node[i * 2 + 1];
            if (i * 2 + 2 < 10)
                node[i].right = node[i * 2 + 2];
        }

        postOrderRe(node[0]);
        System.out.println("***");
        postOrder(node[0]);
    }

    // 后序遍历递归实现
    public static void postOrderRe(TreeNode biTree) {
        if (biTree == null) return;
        else {
            postOrderRe(biTree.left);
            postOrderRe(biTree.right);
            System.out.println(biTree.value);
        }
    }

    public static void postOrder(TreeNode biTree) {//后序遍历非递归实现
        //在辅助栈里表示左节点
        int left = 1;
        //在辅助栈里表示右节点
        int right = 2;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        // 辅助栈，用来判断子节点返回父节点时处于左节点还是右节点。
        Stack<Integer> stack2 = new Stack<Integer>();
        // 将节点压入栈1，并在栈2将节点标记为左节点
        while (biTree != null || !stack.empty()) {
            while (biTree != null) {
                stack.push(biTree);
                stack2.push(left);
                biTree = biTree.left;
            }
            // 如果是从右子节点返回父节点，则任务完成，将两个栈的栈顶弹出
            while (!stack.empty() && stack2.peek() == right) {
                stack2.pop();
                System.out.println(stack.pop().value);
            }
            // 如果是从左子节点返回父节点，则将标记改为右子节点
            if (!stack.empty() && stack2.peek() == left) {
                stack2.pop();
                stack2.push(right);
                biTree = stack.peek().right;
            }

        }
    }
}

// 节点结构
class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;

    TreeNode(int value) {
        this.value = value;
    }
}

4、层次遍历   

与树的前中后序遍历的 DFS 思想不同，层次遍历用到的是 BFS 思想。一般 DFS 用递归去实现（也可以用栈实现），BFS 需要用队列去实现。

层次遍历的步骤是：

•  对于不为空的结点，先把该结点加入到队列中

•  从队中拿出结点，如果该结点的左右结点不为空，就分别把左右结点加入到队列中

•  重复以上操作直到队列为空

    //层次遍历
    public static void levelOrder(TreeNode biTree) {
        if(biTree == null) return;
        LinkedList<TreeNode> list = new LinkedList<TreeNode>();
        list.add(biTree);
        TreeNode currentNode;
        while(!list.isEmpty()) {
            currentNode = list.poll();
            System.out.println(currentNode.value);
            if(currentNode.left != null)
                list.add(currentNode.left);
            if(currentNode.right != null)
                list.add(currentNode.right);
        }
    }