玩具装箱题解 - 洛谷
玩具装箱题解 - cnblogs
斜率优化 - OIWiki
玩具装箱(HAOI2008)
P 教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。
P 教授有编号为 (1 cdots n) 的 (n) 件玩具,第 (i) 件玩具经过压缩后的一维长度为 (C_i)。
为了方便整理,P教授要求:
- 在一个一维容器中的玩具编号是连续的。
- 同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物。形式地说,如果将第 (i) 件玩具到第 (j) 个玩具放到一个容器中,那么容器的长度将为 (x=j-i+sumlimits_{k=i}^{j}C_k)。
制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为 (x),其制作费用为 ((x-L)^2)。其中 (L) 是一个常量。P 教授不关心容器的数目,他可以制作出任意长度的容器,甚至超过 (L)。但他希望所有容器的总费用最小。
设 (f_i) 表示前 (i) 个玩具装箱的最小费用,(s_i) 表示 (c_i) 的前缀和,则有
如一个一个遍历,复杂度为 (O(n^2))。展开后会出现 (-2s_is_j) 这一项,不满足单调队列优化判定式 (displaystyle f_i=min_{j<i}{a_i+b_j})。即需要最小化的多项式和 (i,j) 均有关。
将 (()^2) 括号内与 (i) 有关的设为 (A=s_i+i),与 (j) 有关,或与 (i,j) 均无关的设为 (B=s_j+j+1+L),先不考虑 (min),则有
展开后移项得到
上式只有 (f_i-A^2) 未知。通过考虑其的几何意义,在均摊 (O(1)) 的时间内转移求得最小值,便是「斜率优化」。
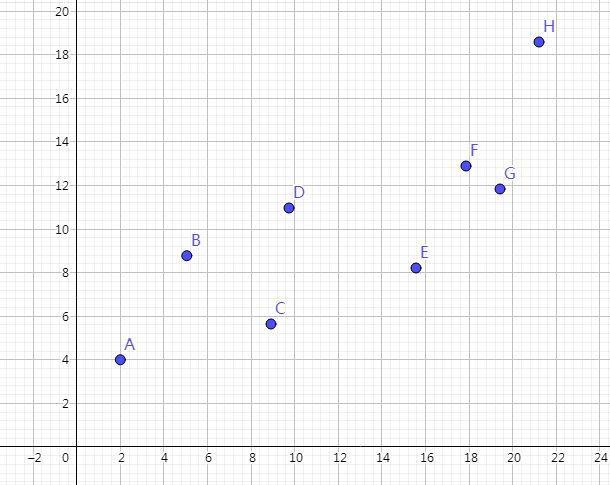
将 ((B,f_j+B^2)) 视作平面中的点,记为 (P_j)。对于 (j),当等式成立时,相当于有一条斜率为 (2A) 的直线经过了点 (P_j)。而这条直线在 (y) 轴上的截距便是 (f_i-A^2)。
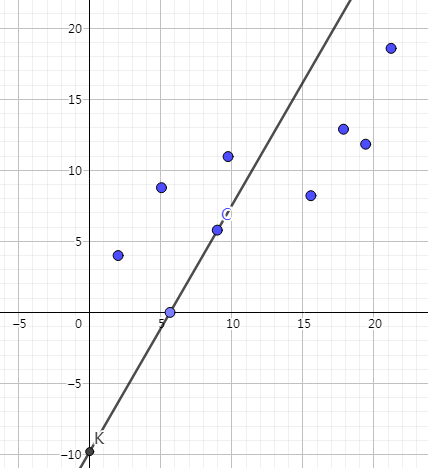
要求出最小的截距,可以把斜率为 (2A) 的直线从下往上平移,直到碰到第一个点,此时的 (y) 轴截距即为最小。
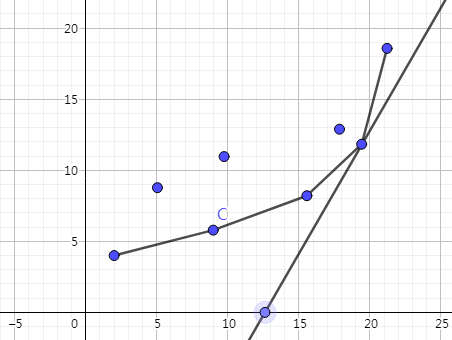
考虑凸包的几何意义(点集的「边界」),可以发现使得截距最小的点一定在点集的下凸包上。
继续观察,还可以发现一个事实。若设构成下凸包的点集为 (S),并从左往右标号为 (S_1,S_2,dots, S_n),设两点 (P_u,P_v) 连成的直线的斜率为 (K(P_u,P_v))。则使得截距最小的点 (S_k) 必满足 (K(S_{k-1},S_k)<2A),(K(S_k,S_{k+1})> 2A)。
凸包本身可以用队列维护。维护方法是在加入一个点 (P_i),判断队尾的点 (P_r) 是否满足 (K(P_r,P_{r-1})>K(P_r,P_i))。如果满足,则弹出 (P_r)。重复此过程直到 (K(P_r,P_{r-1})<K(P_r,P_i)) 或队列中元素不多于一个。
而此题的斜率 (2A) 单调递增,则 (S_k) 左边点的个数也单调递增,所以可以不断 pop 使得 (K(P_l,P_{l+1})<2A) 成立的队头。pop 完之后,队头即为 (S_k)。
此时来归纳一下本题的做法,对于每个点 (P_i):
- 若 (K(P_l,P_{l+1})<2A),则将队头弹出,直到队列中元素数量不多于一个或条件不成立。
- 取出队头,计算 (f_i)。
- 若 (K(P_r,P_{r-1})>K(P_r,P_i)),则弹出队尾,直到队列中元素不多于一个或条件不成立。
- 将 (P_i) 加入队尾。
Code:
- 队列中元素多于一个的「代码意义」为
head < tail。 - 将简化后的式子中的变量用函数写出来。
换成注释里的写法就莫名其妙是错的,可能是因为精度问题,我暂且谔谔。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e4 + 5;
int n, L, q[N], hd, tl;
ll s[N], f[N];
inline double A(int i) { return s[i] + i; }
inline double B(int i) { return s[i] + i + L + 1; }
inline double Y(int i) { return B(i) * B(i) + f[i]; }
inline double X(int i) { return B(i); }
inline double K(int i, int j) { return (Y(j) - Y(i))/(X(j) - X(i)); }
int main() {
ios::sync_with_stdio(false); cin.tie(nullptr);
cin >> n >> L;
for(int i = 1; i <= n; i++)
cin >> s[i], s[i] += s[i - 1];
hd = tl = 1; // 相当于 q[1] = f[0] = s[0] = 0
for(int i = 1; i <= n; i++) {
while(hd < tl && K(q[hd], q[hd + 1]) < 2 * A(i)) ++hd;
f[i] = f[q[hd]] + (ll)(pow((A(i) - B(q[hd])), 2) + 0.1); // 避免精度误差
// f[i] = f[q[hd]] + B(q[hd]) * B(q[hd]) - 2 * A(i) * B(q[hd]) + A(i) * A(i);
while(hd < tl && K(q[tl - 1], q[tl]) > K(q[tl], i)) --tl;
q[++tl] = i;
}
cout << f[n] << '
';
return 0;
}