参考:
https://www.jianshu.com/p/204ed43aec0c
https://blog.csdn.net/qq_27124771/article/details/87651495
https://blog.csdn.net/mazhaMJ/article/details/92629394
桶排序是将待排序集合中处于同一个值域的元素存入同一个桶中,也就是根据元素值特性将集合拆分为多个区域,则拆分后形成的多个桶,从值域上看是处于有序状态的。对每个桶中元素进行排序,则所有桶中元素构成的集合是已排序的。
说简单点,就是:将待排序的数据分到几个有序的桶里,然后对每个桶内的数据单独排序,桶内排完序后,再按顺序依次取出,组成有序序列。
桶排序其实是计数排序的扩展版本,计数排序可以看成每个桶只存储相同元素,而桶排序每个桶存储一定范围的元素,通过映射函数,将待排序数组中的元素映射到各个对应的桶中,对每个桶中的元素进行排序,最后将非空桶中的元素逐个放入原序列中。
快速排序是将集合拆分为两个值域,这里称为两个桶,再分别对两个桶进行排序,最终完成排序。桶排序则是将集合拆分为多个桶,对每个桶进行排序,则完成排序过程。两者不同之处在于,快排是在集合本身上进行排序,属于原地排序方式,且对每个桶的排序方式也是快排。桶排序则是提供了额外的操作空间,在额外空间上对桶进行排序,避免了构成桶过程的元素比较和交换操作,同时可以自主选择恰当的排序算法对桶进行排序。当然桶排序更是对计数排序的改进,计数排序申请的额外空间跨度从最小元素值到最大元素值,若待排序集合中元素不是依次递增的,则必然有空间浪费情况。桶排序则是弱化了这种浪费情况,将最小值到最大值之间的每一个位置申请空间,更新为最小值到最大值之间每一个固定区域申请空间,尽量减少了元素值大小不连续情况下的空间浪费情况。
桶排序过程中存在两个关键环节:
- 元素值域的划分,也就是元素到桶的映射规则。映射规则需要根据待排序集合的元素分布特性进行选择,若规则设计的过于模糊、宽泛,则可能导致待排序集合中所有元素全部映射到一个桶上,则桶排序向比较性质排序算法演变。若映射规则设计的过于具体、严苛,则可能导致待排序集合中每一个元素值映射到一个桶上,则桶排序向计数排序方式演化。
- 排序算法的选择,从待排序集合中元素映射到各个桶上的过程,并不存在元素的比较和交换操作,在对各个桶中元素进行排序时,可以自主选择合适的排序算法,桶排序算法的复杂度和稳定性,都根据选择的排序算法不同而不同。
算法过程
- 根据待排序集合中最大元素和最小元素的差值范围和映射规则,确定申请的桶个数;
- 遍历待排序集合,将每一个元素移动到对应的桶中;
- 对各个桶中元素进行排序,并移动到已排序集合中。
备注:步骤 3 中提到的已排序集合,和步骤 1、2 中的待排序集合是同一个集合。与计数排序不同,桶排序的步骤 2 完成之后,所有元素都处于桶中,并且对桶中元素排序后,移动元素过程中不再依赖原始集合,所以可以将桶中元素移动回原始集合即可。
演示示例
待排序集合为:[-7, 51, 3, 121, -3, 32, 21, 43, 4, 25, 56, 77, 16, 22, 87, 56, -10, 68, 99, 70]
映射规则为:%3D%5Cfrac%20x%7B10%7D-c) ,其中常量位:
,其中常量位: ,即以间隔大小 10 来区分不同值域
,即以间隔大小 10 来区分不同值域
排序算法为:堆排序,根据堆排序特性可知, 个元素的集合,时间复杂度为:
个元素的集合,时间复杂度为: ,算法不保持稳定性
,算法不保持稳定性
映射规则为:
排序算法为:堆排序,根据堆排序特性可知,
step 1:
遍历集合可得,最大值为:,最小值为:
,待申请桶的个数为:
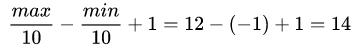
step 2:
遍历待排序集合,依次添加各元素到对应的桶中。
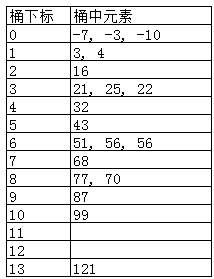
step 3:
对每一个桶中元素进行排序,并移动回原始集合中,即完成排序过程。
算法示例(别问我这是什么语言的代码,我也不懂呃呃呃)
1 def bucketSort(arr): 2 maximum, minimum = max(arr), min(arr) 3 bucketArr = [[] for i in range(maximum // 10 - minimum // 10 + 1)] # set the map rule and apply for space 4 for i in arr: # map every element in array to the corresponding bucket 5 index = i // 10 - minimum // 10 6 bucketArr[index].append(i) 7 arr.clear() 8 for i in bucketArr: 9 heapSort(i) # sort the elements in every bucket 10 arr.extend(i) # move the sorted elements in bucket to array
第一个循环作用为将待排序集合中元素移动到对应的桶中,复杂度为 ) ;第二个循环的作用为对每个桶中元素进行排序,并移动回初始集合中,若桶个数为
;第二个循环的作用为对每个桶中元素进行排序,并移动回初始集合中,若桶个数为  ,平均每个桶中元素个数为
,平均每个桶中元素个数为  ,则复杂度为
,则复杂度为 %3DO(N%2BN(log_2N-log_2M))) 。当
。当  时,即桶排序向计数排序方式演化,则堆排序不发挥作用,复杂度为
时,即桶排序向计数排序方式演化,则堆排序不发挥作用,复杂度为 ) ,只需要将元素移动回初始集合即可。当
,只需要将元素移动回初始集合即可。当  时,即桶排序向比较性质排序算法演化,对集合进行堆排序,并将元素移动回初始集合,复杂度为
时,即桶排序向比较性质排序算法演化,对集合进行堆排序,并将元素移动回初始集合,复杂度为 ) 。
。
算法分析
由算法过程可知,桶排序的时间复杂度为 ,其中
表示桶的个数。
由于需要申请额外的空间来保存元素,并申请额外的数组来存储每个桶,所以空间复杂度为 。
算法的稳定性取决于对桶中元素排序时选择的排序算法。
由桶排序的过程可知,当待排序集合中存在元素值相差较大时,对映射规则的选择是一个挑战,可能导致元素集中分布在某一个桶中或者绝大多数桶是空桶的现象,对算法的时间复杂度或空间复杂度有较大影响,所以同计数排序一样,桶排序适用于元素值分布较为集中的序列。
一个简单明了的例子:

1 public static void bucketSort(int[] arr){ 2 3 // 计算最大值与最小值 4 int max = Integer.MIN_VALUE; 5 int min = Integer.MAX_VALUE; 6 for(int i = 0; i < arr.length; i++){ 7 max = Math.max(max, arr[i]); 8 min = Math.min(min, arr[i]); 9 } 10 11 // 计算桶的数量 12 int bucketNum = (max - min) / arr.length + 1; 13 ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum); 14 for(int i = 0; i < bucketNum; i++){ 15 bucketArr.add(new ArrayList<Integer>()); 16 } 17 18 // 将每个元素放入桶 19 for(int i = 0; i < arr.length; i++){ 20 int num = (arr[i] - min) / (arr.length); 21 bucketArr.get(num).add(arr[i]); 22 } 23 24 // 对每个桶进行排序 25 for(int i = 0; i < bucketArr.size(); i++){ 26 Collections.sort(bucketArr.get(i)); 27 } 28 29 // 将桶中的元素赋值到原序列 30 int index = 0; 31 for(int i = 0; i < bucketArr.size(); i++){ 32 for(int j = 0; j < bucketArr.get(i).size(); j++){ 33 arr[index++] = bucketArr.get(i).get(j); 34 } 35 } 36 }