wikioi 1160 蛇形矩阵

/*========================================================================
1160 蛇形矩阵
题目描述 Description
    小明玩一个数字游戏，取个n行n列数字矩阵（其中n为不超过100的奇数），数字的填补方法为：在矩阵中心从1开始以逆时针方向绕行，逐圈扩大，直到n行n列填满数字，请输出该n行n列正方形矩阵以及其的对角线数字之和.
输入描述 Input Description
    n（即n行n列）
输出描述 Output Description
    n+1行，n行为组成的矩阵，最后一行为对角线数字之和
样例输入 Sample Input
    3
样例输出 Sample Output
    5 4 3
    6 1 2
    7 8 9
    25
数据范围及提示 Data Size & Hint
==========================================================================*/

解析：

下面是n等于7和n等于5的时候数组的样子：

   

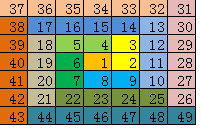
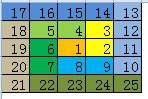
填充数组的方式 如下：

先手动填充数字1（其位置为(n/2,n/2），如上图所示。）
然后一层一层地填充其余部分的数据。（层数m=n/2）
对每一层的填充，按如下顺序处理：

先填充右边这一列（这一列最底下的数据先不填充，下同。）

接着填充上边的横行，然后填充左边这一列，最后填充下边的横行。

（每一段的填充范围如图颜色所示。）

对第x层（1<=x<=m),填充某一段时，该段数据个数为2*x。

比如n=5，第一层每一段的个数是2，第二层每一段的个数是4.

n=7时，第三层每一段的个数是6.

……所以，每一段的循环次数k=2*x。

下面的代码对这一点的处理稍微不同，但本质一样。下面的k从2开始，k/2要小于或等于m即可。

（段与段之间要注意修改坐标）

下面是代码：

#include<stdio.h>
int main()
{
    int i,j,n,a[100][100],k,m,t,p,sum=0;
    scanf("%d",&n);
    i=j=n/2;//最内层的1所在的位置 
    m=n/2;//循环填充的层数（不包括最内层的1） 
    a[i][i]=1;
    t=2;//准备放进数组的数据
    for(k=2;k/2<=m;k=k+2) 
    {
        j=j+1;
        for(p=1;p<=k;p++)//填充右侧这一列
        {
            a[i][j]=t;
            t++;
            i--;
        }
        i++;
        j--;
        for(p=1;p<=k;p++)//填充上边这一横行
        {
            a[i][j]=t;
            t++;
            j--;
        }
        j++;
        i++;
        for(p=1;p<=k;p++)//填充左边这一列
        {
            a[i][j]=t;
            t++;
            i++;
        }
        i--;
        j++;
        for(p=1;p<=k;p++)//填充下面这一横行
        {
            a[i][j]=t;
            t++;
            j++;
        }
        j--;
    }
    for(i=0;i<n;i++)//输出数组顺便求对角线元素的和
    {
        for(j=0;j<n;j++)
        {
            printf("%5d ",a[i][j]);
            if(i==j||i+j==n-1)  sum=sum+a[i][j];
        }
        printf("
");
    }
    printf("%d
",sum);
    return 0;
}