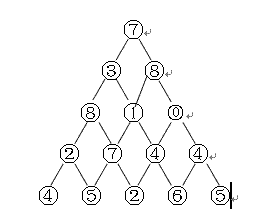
如图所示的数字三角形,从顶部出发,在每一结点可以选择向左走或得向右走,一直走到底层,要求找出一条路径,使路径上的值最大。
第一行是数塔层数N(1<=N<=100)。
第二行起,按数塔图形,有一个或多个的整数,表示该层节点的值,共有N行。
输出最大值。
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
86
解题思路:
参考北大郭炜老师
用二维数组存放数字三角形。
D( r, j) : 第r行第 j 个数字(r,j从1开始算)
MaxSum(r, j) : 从D(r,j)到底边的各条路径中,最佳路径的数字之和。
问题:求 MaxSum(1,1)
典型的递归问题。
D(r, j)出发,下一步只能走D(r+1,j)或者D(r+1, j+1)。故对于N行的三角形:
if ( r == N) MaxSum(r,j) = D(r,j)
else MaxSum( r, j) = Max{ MaxSum(r+1,j), MaxSum(r+1,j+1) } + D(r,j)
下面四段代码分别是存粹递归、记忆型递归、递推、空间优化的递推的代码:
1 #include <stdio.h> 2 3 #define maxN 101 4 5 int N; 6 int D[maxN][maxN]; //D[i][j]表示第i行第 j 个数字。其中i、j从1开始算 7 8 int maxSum[maxN][maxN]; //maxSum[i][j]表示从D(i,j)到底边的各条路径中,最佳路径的数字之和。 9 10 11 //代码一:纯粹递归。当N达到100是绝对是超时的。因为复杂度是O(2^N) 12 int fun1(int i,int j)//返回从(i,j)到达最底层的最大路径之和 13 { 14 if(i==N) return D[i][j]; 15 else 16 { 17 int x=fun1(i+1,j); 18 int y=fun1(i+1,j+1); 19 return D[i][j]+(x>y?x:y); 20 } 21 } 22 23 //代码二:记忆型递归,避免重复计算。时间复杂度O(n*n) 24 int fun2(int i,int j)//返回从(i,j)到达最底层的最大路径之和 25 { 26 if(maxSum[i][j]!=-1) return maxSum[i][j]; 27 28 if(i==N) maxSum[i][j]=D[i][j]; 29 else 30 { 31 int x=fun2(i+1,j); 32 int y=fun2(i+1,j+1); 33 maxSum[i][j]=D[i][j]+(x>y?x:y); 34 } 35 36 return maxSum[i][j]; 37 } 38 39 //代码三:递归变递推 40 int fun3() 41 { 42 int i,j; 43 for(j=1;j<=N;j++) maxSum[N][j]=D[N][j]; 44 45 for(i=N-1;i>=1;i--) 46 { 47 for(j=1;j<=i;j++) 48 { 49 int max=(maxSum[i+1][j]>maxSum[i+1][j+1]?maxSum[i+1][j]:maxSum[i+1][j+1]); 50 maxSum[i][j]=D[i][j]+max; 51 } 52 } 53 return maxSum[1][1]; 54 } 55 56 //代码四:递归变递推并在空间上做优化 57 int fun4() 58 { 59 int i,j; 60 61 for(i=N-1;i>=1;i--) 62 { 63 for(j=1;j<=i;j++) 64 { 65 int max=(D[i+1][j]>D[i+1][j+1]?D[i+1][j]:D[i+1][j+1]); 66 D[i][j]=D[i][j]+max; 67 } 68 } 69 return D[1][1]; 70 } 71 72 int main(int argc, char *argv[]) 73 { 74 int i,j; 75 freopen("001.in","r",stdin); 76 scanf("%d",&N); 77 for(i=1;i<=N;i++) 78 { 79 for(j=1;j<=i;j++) 80 { 81 scanf("%d",&D[i][j]); 82 maxSum[i][j]=-1; 83 } 84 } 85 86 //printf("%d ",fun1(1,1)); 87 //printf("%d ",fun2(1,1)); 88 //printf("%d ",fun3()); 89 printf("%d ",fun4()); 90 return 0; 91 }
补充一个深度优先搜索的实现。仅仅只是演示一下算法,时间复杂度应该是很高,无法AC的。

1 #include<stdio.h> 2 #define maxN 101 3 int n,a[maxN][maxN]={0}; 4 int xx[2]={1,1}; 5 int yy[2]={0,1}; 6 int ans=0,maxAns=0; 7 void dfs(int x,int y) 8 { 9 int i; 10 for(i=0;i<2;i++) 11 { 12 int newX=x+xx[i]; 13 int newY=y+yy[i]; 14 if(newX<=n&&newY<=n) 15 { 16 ans=ans+a[newX][newY]; 17 if(newX==n) 18 { 19 if(ans>maxAns) maxAns=ans; 20 } 21 else dfs(newX,newY); 22 ans=ans-a[newX][newY]; 23 } 24 } 25 } 26 int main() 27 { 28 int i,j; 29 freopen("data.in","r",stdin); 30 scanf("%d",&n); 31 for(i=1;i<=n;i++) 32 for(j=1;j<=i;j++) scanf("%d",&a[i][j]); 33 34 ans=maxAns=a[1][1]; 35 dfs(1,1); 36 37 printf("%d ",maxAns); 38 return 0; 39 }
其实本质和上面递归实现的做法是一致的,只是代码实现框架不同而已。
2193 数字三角形WW
题目链接:http://codevs.cn/problem/2193/
本道题目由上面数字三角形变化而来。具体变化是:从数字三角形顶部往底层走时必须经过某一个指定点,使之走的路程和最大
第1行n,表示n行
第2到n+1行为每个的权值
程序必须经过n div 2,n div 2这个点
最大值
2
1
1 1
2
n <=25
算法分析
这道题只需让必须经过的点的权值加上一个特别大的值,最后的结果再减去这个值就行了。实际上,状态转移方程和上面第一题是没有变的。
我这里在输入时顺便把所有元素累加求和得到sum。然后把这个sum加到必须走的那个点。
1 #include <stdio.h> 2 #define maxN 101 3 int n,a[maxN][maxN]; 4 int main(int argc, char *argv[]) 5 { 6 int i,j,x,y,sum=0; 7 scanf("%d",&n); 8 for(i=1;i<=n;i++) 9 for(j=1;j<=i;j++) 10 { scanf("%d",&a[i][j]); sum=sum+a[i][j]; } 11 x=n/2; y=n/2; 12 a[x][y]+=sum; 13 for(i=n-1;i>=1;i--) 14 { 15 for(j=1;j<=i;j++) 16 { 17 a[i][j]+=(a[i+1][j]>a[i+1][j+1]?a[i+1][j]:a[i+1][j+1]); 18 } 19 } 20 printf("%d ",a[1][1]-sum); 21 return 0; 22 }
2198 数字三角形WWW
题目链接:http://codevs.cn/problem/2198/
本道题目由上面第一题数字三角形变化而来。具体变化是:从数字三角形必须经过某一个点,使之走的路程和最大
第1行n,表示n行
第2到n+1行为每个的权值
第n+2行为两个数x,y表示必须经过的点
最大值
2
1
1 1
1 1
2
n<=25
算法分析
这个题目和第二题并没什么区别,唯一区别就是输入时多输入x和y表示必须要走过的点。
1 #include <stdio.h> 2 #define maxN 101 3 int n,a[maxN][maxN]; 4 int main(int argc, char *argv[]) 5 { 6 int i,j,x,y,sum=0; 7 scanf("%d",&n); 8 for(i=1;i<=n;i++) 9 for(j=1;j<=i;j++) 10 { scanf("%d",&a[i][j]); sum=sum+a[i][j]; } 11 //x=n/2; y=n/2; 12 scanf("%d%d",&x,&y); 13 a[x][y]+=sum; 14 for(i=n-1;i>=1;i--) 15 { 16 for(j=1;j<=i;j++) 17 { 18 a[i][j]+=(a[i+1][j]>a[i+1][j+1]?a[i+1][j]:a[i+1][j+1]); 19 } 20 } 21 printf("%d ",a[1][1]-sum); 22 return 0; 23 }
上面三道题目的代码中用到的动规状态转移方程都是逆推,从最后一行往前递推。其实也是可以顺着推的。比如第三题的代码可以像下面这一段这么写:(下面代码中,f[i][j]表示的是从(i,j)这个点到达(1,1)这个点的最大路径之和。另外,这里用了两个数组,其实仅用一个数组即可,类似上述代码。)
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 int n,x,y,w[35][35],ko; 6 long long f[35][35]; 7 int main() 8 { 9 scanf("%d",&n); 10 for(int i=1;i<=n;i++) 11 for(int j=1;j<=i;j++) 12 scanf("%d",&w[i][j]); 13 scanf("%d%d",&x,&y); 14 w[x][y]+=99999999; 15 f[1][1]=w[1][1]; 16 for(int i=2;i<=n;i++) 17 for(int j=1;j<=i;j++) 18 f[i][j]=w[i][j]+max(f[i-1][j],f[i-1][j-1]); 19 long long ans=0; 20 for(int i=1;i<=n;i++) 21 ans=max(ans,f[n][i]); 22 printf("%lld",ans-99999999); 23 return 0; 24 }
2189 数字三角形W
题目链接:http://codevs.cn/problem/2189/
这个题目仍然是由上面第一题的数字三角形变化而来。具体如下:
数字三角形
要求走到最后mod 100最大
第1行n,表示n行
第2到n+1行为每个的权值
mod 100最大值
2
1
99 98
99
n<=25
算法分析
这个题目的改动使得问题处理起来比较麻烦了。本来比较大的一个数,加上那么一点点,再取模,可能就很小了。显然这已经不再满足动态规划的无后效性原则了。怎么办呢?
可以开一个布尔型的三维数组,用f[i][j][k]表示走到位置(i,j)时路径权值之和再取模能否得到k这个值,于是得到这样一个状态转移方程:
f[i][j][k]=f[i][j][k] or f[i-1][j][(k-a[i][j]+m)%m] or f[i-1][j-1][(k-a[i][j]+m)%m],这里面加上m是为了防止出现负下标。
最后找一遍那个目标状态存在就行了。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=26; 6 int n; 7 int a[MAXN][MAXN]; 8 bool f[MAXN][MAXN][101]; 9 int main() 10 { 11 scanf("%d",&n); 12 for(int i=1;i<=n;i++) 13 for(int j=1;j<=i;j++) 14 cin>>a[i][j]; 15 16 for(int i=1;i<=n;i++)f[n][i][a[n][i]%100]=1; 17 18 for(int i=n-1;i>=1;i--) 19 for(int j=1;j<=i;j++) 20 for(int k=0;k<=99;k++) 21 f[i][j][k]=f[i+1][j][(k-a[i][j]+100)%100]||f[i+1][j+1][(k-a[i][j]+100)%100]; 22 23 for(int k=100;k>=1;k--) 24 if(f[1][1][k]==1){cout<<k;break;} 25 return 0; 26 }
下面这一段代码可能比较好理解:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 int n,a[26][26]={0}; 6 bool f[26][26][102]={0}; 7 int main() 8 { 9 cin>>n; 10 for (int i=1;i<=n;i++) //数据的读入 11 for (int j=1;j<=i;j++) 12 cin>>a[i][j]; 13 14 for (int i=1;i<=n;i++) //这一步的代码是为了将最后一排的所有数存下来 15 f[n][i][a[n][i]]=true; 16 17 for (int i=n-1;i>=1;--i) //这里是主要过程,思路:将所有的可能性mod100都存下来, 18 for (int j=1;j<=i;j++) 19 for (int k=0;k<=99;k++) 20 { 21 if (f[i+1][j][k]) f[i][j][(k+a[i][j])%100]=true; 22 if (f[i+1][j+1][k]) f[i][j][(k+a[i][j])%100]=true; 23 } 24 for (int k=99;k>=0;--k) //找出所有可能性中最大的可能,输出,这个题就AC咯、 25 if (f[1][1][k]) 26 { 27 cout<<k; 28 return 0; 29 } 30 }
4829 [DP]数字三角形升级版 & 4832 [DP]数字三角形升级版
(ps:两道题其实是一样的,据说数据规模不同)
题目仍然是由上面第一题的数字三角形变化而来,具体如下:
从数字三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,且你有一次机会可以把任何一个数重复加一遍。
和最大的路径称为最佳路径。你的任务就是求出最佳路径上的数字之和。
第一行:一个数,表示行数。
接下来n行为数塔
一个数即最优结果
5
1
1 3
1 1 3
1 1 1 3
7 1 1 1 3
18
三角形行数不大于1000。最大和不大于maxlongint
算法分析
这个似乎有点类似于背包问题的回溯法求解。可以对动规数组增加一维,用于记录从底层到达(i,j)这个位置的路径上是否曾经有数字被重复使用过。具体参见以下代码:
(代码来自codevs讨论版块)
1 #include<iostream> 2 using namespace std; 3 int n; 4 int a[1000][1000]; 5 int f[1000][1000][2]; 6 int i,j; 7 int main() 8 { 9 cin>>n; 10 for(i=0;i<n;i++) 11 for(j=0;j<=i;j++)cin>>a[i][j]; 12 for(i=0;i<n;i++){ 13 f[n-1][i][0]=a[n-1][i]; 14 f[n-1][i][1]=a[n-1][i]<<1;//f[n-1][i][1]=a[n-1][i]*2; 15 } 16 for(i=n-2;i>=0;i--) 17 for(j=0;j<=i;j++){ 18 f[i][j][0]=a[i][j]+max(f[i+1][j][0],f[i+1][j+1][0]); 19 f[i][j][1]=a[i][j]+max(f[i+1][j][1],f[i+1][j+1][1]); 20 f[i][j][1]=max(f[i][j][1],f[i][j][0]+a[i][j]); 21 } 22 cout<<f[0][0][1]<<endl; 23 return 0; 24 }
再补充一道数字三角形变形的题目:
关于数字三角形,还有一题:5585 数字三角形第k优解,暂时未搞懂怎解,希望各位大神留言解答呵呵。
参考资料:
【强烈建议阅读】http://blog.csdn.net/Little_Flower_0/article/details/47945611
【强烈建议阅读】http://blog.csdn.net/qq_35776409/article/details/62890528
http://www.cnblogs.com/zwfymqz/p/6790960.html
http://www.genshuixue.com/i-cxy/p/8020923
