- 总时间限制: 1000ms 内存限制: 65536kB
- 描述
-
有一块矩形大蛋糕,长和宽分别是整数w 、h。现要将其切成m块小蛋糕,每个小蛋糕都必须是矩形、且长和宽均为整数。切蛋糕时,每次切一块蛋糕,将其分成两个矩形蛋糕。请计算:最后得到的m块小蛋糕中,最大的那块蛋糕的面积下限。
假设w= 4, h= 4, m= 4,则下面的切法可使得其中最大蛋糕块的面积最小。
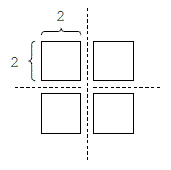
假设w= 4, h= 4, m= 3,则下面的切法会使得其中最大蛋糕块的面积最小:

- 输入
- 共有多行,每行表示一个测试案例。每行是三个用空格分开的整数w, h, m ,其中1 ≤ w, h, m ≤ 20 , m ≤ wh. 当 w = h = m = 0 时不需要处理,表示输入结束。
- 输出
- 每个测试案例的结果占一行,输出一个整数,表示最大蛋糕块的面积下限。
- 样例输入
-
4 4 4 4 4 3 0 0 0
- 样例输出
-
4 6
算法分析:
直接枚举DP
f[i][j][k]表示把i*j分成k块蛋糕时,最大的那块蛋糕的面积下限(最小值)。
枚举横切竖切形成的新蛋糕即可
1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 #define N 25 5 #define INF 5005 6 int f[N][N][N];int w,h,m; 7 int main(){ 8 w=h=m=20; 9 for(int i=1;i<=w;i++){ 10 for(int j=1;j<=h;j++){ 11 f[i][j][1]=i*j; 12 for(int k=2;k<=m;k++){ 13 f[i][j][k]=INF; 14 for(int r=1;r<i;r++){ 15 f[i][j][k]=min(f[i][j][k],max(f[r][j][k-1],(i-r)*j)); 16 for(int p=1;p<k;p++) 17 f[i][j][k]=min(f[i][j][k],max(f[r][j][p],f[i-r][j][k-p])); 18 } 19 20 for(int c=1;c<j;c++){ 21 f[i][j][k]=min(f[i][j][k],max(f[i][c][k-1],(j-c)*i)); 22 for(int p=1;p<k;p++) 23 f[i][j][k]=min(f[i][j][k],max(f[i][c][p],f[i][j-c][k-p])); 24 } 25 } 26 } 27 } 28 while(scanf("%d%d%d",&w,&h,&m)&&(w||h||m)){ 29 printf("%d ",f[w][h][m]);} 30 return 0; 31 }
来源:http://blog.csdn.net/qq_18455665/article/details/50512764