贝叶斯算法是一个典型的统计概率学算法,里面涉及到较多的统计学概念,贝叶斯分类器和贝叶斯网络也是以这个算法作为理论基础。先来看看几个绕不过去的统计学概念:
先验概率:事件发生前的预判概率,可以是基于历史数据统计,也可以由背景常识得出,一般是单独事件概率,如P(A) - 这个幼儿园男孩比例是多少、P(B)-这个幼儿园女孩比例是多少。
后验概率:事件发生后求的反向条件概率,在给定条件C以后,A发生的概率 P(A|C)- 有一个小孩会唱歌,请问他(她)是男孩的概率有多大(幼儿园中1/2的男孩会唱歌,2/3的女孩会唱歌)。
极大似然估计:就是利用已知的样本结果信息,反推最具可能(最大概率)导致这些样本结果出现的模型参数值。
贝叶斯分类的原理就是通过先验概率,利用贝叶斯公式计算出后验概率,选择最大后验概率所对应的分类结果。
经典贝叶斯公式:
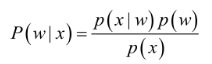
P(w)为先验概率,表示每种类别分布的概率;
P(x|w)为类条件概率,表示在某种类别前提下,某事发生的概率;
P(x)是用于归一化的证据因子,对于给定样本,证据因子与类标记无关;
P(w|x)为后验概率,表示某事已经发生了,它属于某一类别的概率,我们就是要找出后验概率最大的类别,作为分类的结果。
我们来看一个简单的例子:已知,在幼儿园中,会唱歌的男孩占男孩总数的1/2,会唱歌的女孩占女孩总数的2/3,并且幼儿园中男女比例为2:1,试问一个会唱歌的小孩为男孩和女孩的概率各为多少?
假设: w1=男孩,w2=女孩,x=会唱歌
先验概率 P(w1)=2/3,P(w2)=1/3
类条件概率 P(x|w1)=1/2, P(x|w2)=2/3
男孩和女孩会唱歌相互独立,P(x)= P(x|w1)P(w1) + P(x|w2)P(w2) = 5/9
根据贝叶斯公式计算出男孩和女孩的概率分别是60%和40%。(如果只考虑分类问题,只需要比较后验概率的大小,不用计算具体的值,所以P(x)的取值不重要)
通过上面的例子,我们就把通过贝叶斯公式进行分类的问题简化为通过训练数据来估计先验概率P(w)和类条件概率P(x|w)。
P(w)表达的是样本空间内各类样本所占的比例,通过简单的统计就可以计算出来,关键是类条件概率P(x|w)怎么确定。但类条件概率的估计非常困难,因为这是一个涉及到w所有属性的联合概率,但我们的数据量有限,不是所有样本取值都在数据集中出现,直接根据样本出现的频率来确定类条件概率P(x|w)会产生较大的偏差。
那怎么确定类条件概率呢,这里就要引入“极大似然估计”方法了,这是一种参数估计的方法:先假定其具有某种确定的概率分布形式(概率模型),再基于训练样本对概率分布的参数进行估计,简单来说,就是“先确定概率模型,再根据数据训练找到使得概率最大的模型参数”。
对于P(x|a)这个函数,x表示某一个具体的数据,a表示模型的参数。
如果a是已知的,x是变量,这个函数叫做概率函数,它描述对于不同的样本点x,其出现的概率是多少;
如果x是已知的,a是变量,这个函数叫做似然函数,它描述对于不同的模型参数,出现x这个样本点的概率是多少。我们需要求解的是后一种情况,所以这个过程叫做“极大似然估计”
-- 朴素贝叶斯分类
朴素贝叶斯假设所有属性相互独立,各属性独立地对分类结果发生影响,互不干扰。
朴素贝叶斯分类的基本过程:
1、数据集 X = {a1,a2,..... am}为待分类项,每个a为数据集X的一个特征属性;
2、有类别集合C = {y1,y2,... yn}
3、计算类条件概率 P(y1|x),P(y2|x),..... P(yn|x)
4、判断如果 P(yk|x)= max{P(y1|x),P(y2|x),..... P(yn|x)},则x属于yk
整个过程的难点在于第三步,计算各个类的条件概率,根据贝叶斯定理和朴素贝叶斯的假设,贝叶斯公式可以转化为如下表示:
(1)离散特征值处理
当特征属性为离散值时,P(x=xi|Y=c)= Dc,xi/Dc
Dc,xi: 类别为c中属性xi=x的样本总数
Dc:类别为c的样本总数
(2)连续特征值处理
假设连续变量服从某种概率分布(假设概率模型),然后使用训练数据估计概率模型的参数。
假设特征变量符合高斯分布,对于每个类别yi,特征属性Xi的类条件概率为:
其中和分别是第i类样本在第j个属性上取值的均值和方差,极大似然估计就是估计这两个参数。
朴素贝叶斯常用的几个模型分别为:
1、高斯模型(多用于连续值);
2、多项式模型(多用于离散值);
3、伯努利模型(也用于离散特征中,但每个特征的取值只能是0或1)
-- 朴素贝叶斯特点:
优点:
1、发源于古典数学理论,效率较高;
2、对小规模数据训练效果较好,适合多分类任务,适合增量训练;
3、算法简单,易于实现,常用于文本分类;
缺点:
1、朴素贝叶斯假设属性之间相互独立,但在实际情况中,属性较多或者属性相关性较大时,分类效果不好;
2、需要先假设先验概率,假设的模型有很多种,可能会由于选择的概率模型的原因导致分类效果不佳。
-- sklearn朴素贝叶斯分类
用20twenty news数据集为例进行文本分类的练习 ,一共20个新闻类别,20000篇新闻数据,利用朴素贝叶斯算法进行模型训练,示例代码如下:
from sklearn import metrics
from sklearn.datasets import load_files
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.naive_bayes import MultinomialNB
import numpy as np
#################### 20twenty_new ##########################
# categories = ['alt.atheism', 'soc.religion.christian', 'comp.graphics', 'sci.med']
twenty_train = load_files("20news-bydate-train", shuffle=True, encoding='latin1',random_state=42)
twenty_test = load_files("20news-bydate-test", shuffle=True, encoding='latin1',random_state=42)
count = CountVectorizer()
tfidf_transformer = TfidfTransformer()
count_vect = CountVectorizer()
X_train_counts = count_vect.fit_transform(twenty_train.data)
tfidf_transformer = TfidfTransformer()
X_train_tfidf = tfidf_transformer.fit_transform(X_train_counts)
'''
使用朴素贝叶斯分类(多项式分布),并做出简单的预测
'''
clf_Multi = MultinomialNB().fit(X_train_tfidf, twenty_train.target)
docs_test = twenty_test.data
X_test_counts = count_vect.transform(docs_test)
X_test_tfidf = tfidf_transformer.transform(X_test_counts)
predicted = clf_Multi.predict(X_test_tfidf)
print(metrics.classification_report(twenty_test.target, predicted, target_names=twenty_test.target_names))
print("accurary " + str(np.mean(predicted == twenty_test.target)))
=======================================================================
precision recall f1-score support
alt.atheism 0.80 0.52 0.63 319
comp.graphics 0.81 0.65 0.72 389
comp.os.ms-windows.misc 0.82 0.65 0.73 394
comp.sys.ibm.pc.hardware 0.67 0.78 0.72 392
comp.sys.mac.hardware 0.86 0.77 0.81 385
comp.windows.x 0.89 0.75 0.82 395
misc.forsale 0.93 0.69 0.80 390
rec.autos 0.85 0.92 0.88 396
rec.motorcycles 0.94 0.93 0.93 398
rec.sport.baseball 0.92 0.90 0.91 397
rec.sport.hockey 0.89 0.97 0.93 399
sci.crypt 0.59 0.97 0.74 396
sci.electronics 0.84 0.60 0.70 393
sci.med 0.92 0.74 0.82 396
sci.space 0.84 0.89 0.87 394
soc.religion.christian 0.44 0.98 0.61 398
talk.politics.guns 0.64 0.94 0.76 364
talk.politics.mideast 0.93 0.91 0.92 376
talk.politics.misc 0.96 0.42 0.58 310
talk.religion.misc 0.97 0.14 0.24 251
avg / total 0.82 0.77 0.77 7532
accurary 0.77389803505
作者:华为云专家周捷
@All开发者,想获取满满的技术干货吗?想了解最前沿的技术洞察吗?想得到最权威的学习认证吗?还有多维的交流平台以及有趣的有奖互动?
2020年华为开发者大会将于2月11-12日在深圳举办,这将是华为面向开发者群体的最顶级盛会,包含但不限于华为在云计算、人工智能、5G、IoT等多个领域,特别是智能计算双引擎鲲鹏和昇腾的最新创新与最佳实践,充满期待对吧,欢迎报名预约!