摘要:平时练习算法题学习算法知识时,经常会发现题解里写着“动态规划”,里面一上来就是一个复杂的dp公式,对于新人来说除了说声“妙啊”,剩下就是疑惑,他是怎么想到这个公式的?我能想到吗?这玩意工作中有用吗?
本文分享自华为云社区《动态规划究竟是怎么想到的?【奔跑吧!JAVA】》,原文作者:breakDraw。
平时练习算法题学习算法知识时,经常会发现题解里写着“动态规划”,里面一上来就是一个复杂的dp公式,对于新人来说除了说声

剩下就是疑惑,他是怎么想到这个公式的?我能想到吗?这玩意工作中有用吗?
加上“动态规划”这高端的名字,然后就劝退了不少试图去理解他的人。

动态规划听起来太吓人,可以换个说法
我在内心更喜欢叫他“状态缓存”
如果是服务开发,相信很熟悉这个词语, 利用缓存来加快一些重复的请求的响应速度。
而这个缓存的特点是 和其他缓存有所关联。
比如我们的服务要计算7天内的某金钱总和,计算后要缓存一下。
后来又收到一个请求,要计算8天内的金钱总和
那我们只需要取之前算过的7天内的金钱综合,加上第8天的金钱就行了。
1+4的思考套路
自己针对动态规划总结了一个自己的思考套路,我叫他1组例子4个问题,就叫1+4好了,通过这5个过程,可以站在普通人的角度(就是非acm大佬那种的角度),去理解动态规划是如何被思考出来的
- 在超时的思路上写出一组计算过程的例子
- 在超时例子的基础上,有哪些重复、浪费的地方?
- 如何定义dp数组
- 状态的变化方向是什么,是怎么变化的
- 边界状态是什么
简单例子
以一道简单题为例:
爬楼梯:
https://leetcode-cn.com/problems/climbing-stairs/
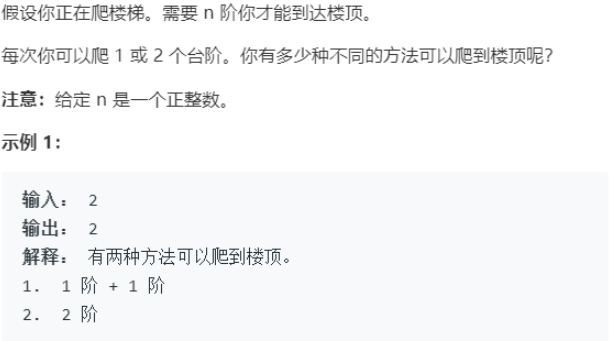
这时候就要静下心,观察这个解法的例子中是否有重复经历的场景,而这个重复经历的场景就叫状态。
我处理动态规划的题目时, 都会问自己3个问题,一般就能顺利地解决。
①在超时的思路上写出一组计算过程的例子
如果我们考虑最简单的解法, 就是从起点开始,每次选择走1步或者走2步,看下能否走到终点,能走到则方法数+1。
但这种方法注定超时(O(n^2))
但我还是照着这个过程模拟了一下,随便列了几个
1 ->2-> 3-> 4-> 5
1 ->2 ->3-> 5
1->3->4->5
1->3->5
②在超时例子的基础上,有哪些重复、浪费的地方?
在上面,我发现了重复的地方

也就是说
从3到5总共就2种路线,已经在1->2之后计算过了,我后面从1走到3再往后走时,没必要再去算了。
换言之,当我走到3的时候,其实早就可以知道后面还剩下多少种走法。
发现重复的地方后,就可以开始建立dp公式了。
③如何定义dp数组?
定义dp数组,也就是定义上面提到的重复的地方。重新看下之前的那句话
当我走到3的时候,其实早就可以知道后面还剩下多少种走法。
所以dp[3]代表的就是从3往后,有多少种可走的方法。
④状态的变化方向是什么,是怎么变化的
- 首先思考状态的变化方向
重新看这句话:
当我走到3的时候,其实早就可以知道后面还剩下多少种走法
说明结果取决于往 后面 的状态
因此我们要先计算后面的状态, 即从后往前算
- 接着思考这个后面的状态和当前的状态有什么联系,是怎么变化的
这个一般都包含在题目条件中
根据题意,要么走2步,要么走1步,因此每当我走到一层时,下一次就2种状态可以变化。
那么对于第3层而言,他后续有2种走法,走1步或者走2步
那么他的情况就是dp[3] = dp[3+1] + dp{3+2}
如果层数设为i,那么这个变化情况就是
dp[i] = dp[i+1] + dp[i+2]
⑤边界状态是什么?
边界状态就是不需要依赖后面的状态了,直接可以得到结果的状态。
在这里肯定就是最后一层dp[n], 最后一层默认是一种走法。 dp[n]=1
实现
根据上面的过程,自己便定义了这个状态和变化
- 定义:dp[i] : 代表从第i层往后,有多少种走法
- 方向和变化:dp[i] = dp[i+1] + dp[i+2];
- 边界: dp[n] = 1
根据这个写代码就很容易了
代码:
public int climbStairs(int n) { int[] dp = new int[n + 1]; dp[n] = 1; dp[n-1] = 1; for(int i = n-2; i >=0;i--) { dp[i] = dp[i+1] + dp[i+2]; } return dp[0]; }
进阶版,二维的动态规划
https://leetcode-cn.com/problems/number-of-ways-to-stay-in-the-same-place-after-some-steps/

①在超时的思路上写出一组计算过程的例子
超时的思路肯定是像搜索一样模拟所有的行走过程。
先假设1个steps=5, arrlen=3的情况
随便先列几个。模拟一下不断走的位置。数字指的是当前位置。
0->1->2->1->0->0
0->1->2->1->1->0
0->1->1->1->1->0
0->1->1->1->0->0
0->0->1->1->1->0
……
②在超时例子的基础上,有哪些重复、浪费的地方?
0->1->2->1->0->0
0->1->2->1->1->0
0->1->1->1->1->0
0->1->1->1->0->0
0->0->1->1->1->0
0->0->1->1->0->0
我发现这部分标粗的部分重复了,
换句话说
当我还剩2步且当前位置为1的时候,后面还有多少种走法,其实早就知道了。
③如何定义dp数组?
重新看这句话:
当我还剩2步且当前位置为1的时候,后面还有多少种走法,其实早就知道了。
涉及了2个关键因素: 剩余步数和当前值,所以得用二维数组
因此
dp[realstep][index]
就代表了 剩余步数为step且位置为index时, 后续还剩多少种走法。
④状态的变化方向是什么,是怎么变化的
- 先思考变化方向
“当我还剩2步且当前位置为1的时候,后面 还有多少种走法,其实早就知道了。”
这个后面是指啥, 后面会怎么变?
后面肯定是步数越来越少的情况, 并且位置会根据规律变化。 所以变化方向是步数变少,位置则按照规定去变。
那么这个固定越来越少的这个“剩余步数”,就是核心的变化方向。
我们计算时,可以先计算小的剩余步数的状态, 再去算大的剩余步数。
- 如何变化
根据题意和方向,剩余步数肯定-1, 然后位置有3种选择(减1,不变,加1), 那么方法就是3种选择的相加。
dp[step][index] = dp[step-1][index-1] + dp[step-1][index] + dp[step-1][index+1]
⑤边界状态是什么?
剩余步数为0时,只有当前位置为0才是我们最终想要的方案,把值设为1并提供给后面用,其他位置且步数为0时都认为是0。
dp[0][0] = 1;
dp[0][index] = 0;(index>0)
实现
那么最终出来了
- 定义:dp{realstep][index]: 剩余步数为step且位置为index时, 后续还剩多少种走法。
- 方向和变化:dp[step][index] = dp[step-1][index-1] + dp[step-1][index] + dp[step-1][index+1]
- 边界: dp[0][0] = 1;
内存溢出处理
不过这题因为是困难题,所以给上面这个公式设立了一个小难度:
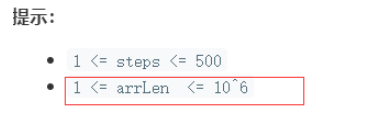
数组长度非常大,导致如果index的范围我们选择为0~arrLen-1, 那么最大情况dp[500][10^6]注定超时内存范围。
这时候就要去思考index设那么大是不是没必要
一般我们可以自己列这种情况的小例子,例如
step=2, arr=10
然后看下index有没有必要设成0~9,随便走几步
0->1->0
0->1->0
0->0->0
嗯?我发现就3种情况,arr后面那么长不用啦?
于是发现规律:
剩余的步数,必须支撑他返回原点!
也就是说,其实index的最大范围最多就是step/2, 不能再多了,再多肯定回不去了。
于是问题解决。
其他类似题目练习
https://leetcode-cn.com/problems/minimum-cost-for-tickets/