Codeforces round 699 赛后解题报告
本场比赛前 \(3\) 题的背景还不错,后面不知道有啥关联性。。。
A. Space Navigation
赛时我关注了一下做出提的人数,我在 6min 的时候提交,一次通过,但此时只有大概 800 个人通过,有点令人大跌眼镜。
分析题目,我们其实可以根据 \(s\) 算出这个飞船在 \(x\) 轴正负方向上和 \(y\) 轴正负方向上最远可以到达的坐标位置,四个量算出来后,和目的地的坐标一比较,答案自现。
//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,u,d,l,r,m;
signed main() {
int t=read();
while(t--) {
cin>>n>>m;
string s;
cin>>s;
int sz=s.size();
u=l=d=r=0;
for(int i=0;i<sz;i++) {
if(s[i]=='U') {
u++;
}
if(s[i]=='D') {
d++;
}
if(s[i]=='L') {
l++;
}
if(s[i]=='R') {
r++;
}
}
if(n>0) {
if(r<n) {
printf("NO\n");
continue;
}
}
else {
if(l<(-n)) {
printf("NO\n");
continue;
}
}
if(m>0) {
if(u<m) {
printf("NO\n");
continue;
}
}
else {
if(d<(-m)) {
printf("NO\n");
continue;
}
}
printf("YES\n");
}
return 0;
}
B. New Colony
本题我在 14min 时通过,当时只有 647 人通过。
本题 \(k\) 很大,其实是个纸老虎。我们想最简单的,如果有一次我的石头滚到了 \(n+1\) 处,那么下一个,还会滚到 \(n+1\) 处,因此我们只需要一直模拟,直到有石头滚到 \(n+1\) 时,退出循环,答案为 \(-1\)。若 \(k\) 次前,没有滚到 \(n+1\) 处,把模拟得出的答案输出即可,可以证明,时间复杂度为 \(O(\sum hn)\)
//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int MAXN=100+10;
int n,h[MAXN],k;
signed main() {
int t=read();
while(t--) {
n=read();k=read();
for(int i=1;i<=n;i++) {
h[i]=read();
}
h[n+1]=0;
bool flag=1;
int pos;
while(k--&&flag) {
pos=1;
while(pos<=n&&h[pos]>=h[pos+1]) {
pos++;
}
h[pos]++;
if(pos==n+1) {
flag=0;
pos=-1;
}
}
cout<<pos<<endl;
}
return 0;
}
C. Fence Painting
本题细节较多,因此我在 45min 通过时,只有 600 人左右通过。
首先容易想到倒序考虑,因为后来者的颜色肯定在上面。我们可以记录一下 \(a,b\) 中有多少颜色需要更换,有哪些颜色不需要更换。我们在考虑颜色时,首先考虑的就是那些需要更改的颜色,如果现在要考虑的颜色已经不再需要了,就选择下一个要涂的人所涂的那个栅栏即可,这样下一个人会盖过现在的颜色。
细节贼多,注意数组清空。
//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int MAXN=1e5+10;
int n,m,a[MAXN],b[MAXN],c[MAXN],ans[MAXN],tot;
stack<int> cnt[MAXN];
int ex[MAXN];
signed main() {
int t=read();
while(t--) {
n=read();m=read();
tot=0;
for(int i=1;i<=n;i++) {//细节,清空数组
int sz=cnt[i].size();
while(sz--) {
cnt[i].pop();
}
ex[i]=0;
}
for(int i=1;i<=n;i++) {
a[i]=read();
}
for(int i=1;i<=n;i++) {
b[i]=read();
if(b[i]!=a[i]) {
if(cnt[b[i]].empty()) {
tot++;//有多少种颜色需要更改
}
cnt[b[i]].push(i);
}
ex[b[i]]=i;//记录那些颜色出现
}
for(int i=1;i<=m;i++) {
c[i]=read();
}
int last=0;
bool flag=1;
for(int i=m;i;i--) {
if(!cnt[c[i]].empty()) {
ans[i]=cnt[c[i]].top();
cnt[c[i]].pop();
if(cnt[c[i]].empty()) {
tot--;
}
}
else {
if(last==0) {
//即考虑最后一个粉刷匠,单独处理
if(ex[c[i]]) {
ans[i]=ex[c[i]];
}
else {
//没地方画,输出NO
printf("NO\n");
flag=0;
break;
}
}
else {
ans[i]=last;
}
}
last=ans[i];
}
if(flag&&tot) {
//若颜色不够用,没有改好,输出NO
printf("NO\n");
}
else if(flag){
printf("yEs\n");
for(int i=1;i<=m;i++) {
printf("%lld ",ans[i]);
}
cout<<endl;
}
}
return 0;
}
D. AB Graph
我是SB。
比赛的时候由于有一种情况没有输出 Yes,挂了,赛后加上就过了。
而且话说这天早上刚考完 WC2021。不觉得WC的这道题和他很像吗。我当时吓出一身冷汗。
好啦不说废话,来分析本题。我们不要把它想得过于复杂,我们分成几种情况。我们令 \(w(u,v)\) 为从 \(u\) 出发,到 \(v\) 的这条边上的字符,令 \(x,y\) 表示这两种字符。
如果存在某两点 \(u,v\),使得 \(w(u,v)\) 和 \(w(v,u)\) 相同,那么我们可以对于任意 \(m\),构造出形如 \(u,v,u,v,u,\cdots\) 的答案,最后的串为 \(x,x,x\cdots\)。显然回文。
如果不存在,说明一定是两点之间的边,有为 a 的,也有为 b 的。如果 \(m\) 为奇数,那么随便找两点我们可以构造如下答案 \(u,v,u,v,\cdots,u,v\),那么经过的边形成的串为 \(x,y,x,\cdots,y,x\),明显回文。
我们只需要处理剩下的 \(m\) 为偶数的情况。我们需要找到如下图的结构:
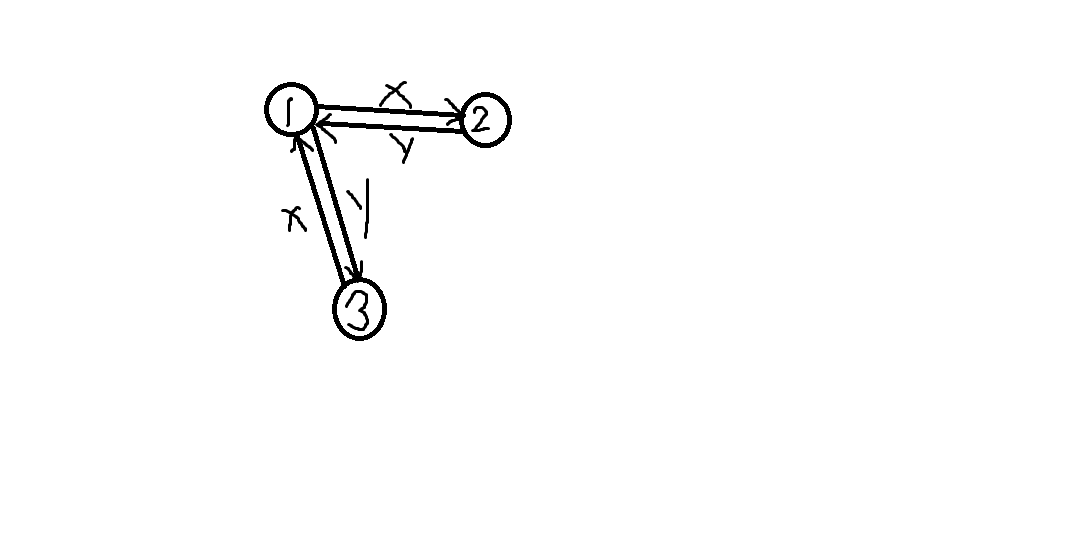
我们可以在 \(O(n^2)\) 的时间内找到这样的 \(1,2,3\)。易证,在目前讨论的大前提下,对于任意 \(n\geq 3\),都能至少找出一组这样的结构。我们可以构造出以下两种答案,根据 \(m\) 模 \(4\) 的余数决定选择哪一种。
- 第一种,经过的点为 \(3,1,2,1,3,1,2,3,\cdots,3,1,2,1,3,1,2\),得到的串为 \(x,x,y,y,x,x,\cdots,x,x\)。显然回文。
- 第二种,经过的点为 \(1,3,1,2,1,3,1,2,\cdots,1,3,1,2,1\),得到的串为 \(y,x,x,y,y,x,x,y,\cdots,y,x,x,y\)。显然回文。
其他情况输出 NO。
//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include<bits/stdc++.h>
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int MAXN=1e3+10;
int n,m;
char ch[MAXN][MAXN];
signed main() {
int t=read();
while(t--) {
n=read();
m=read();
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
cin>>ch[i][j];
}
}
bool flag=0;
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
if(i!=j&&ch[i][j]==ch[j][i]) {
printf("YES\n");
for(int k=1;k<=m;k+=2) {
printf("%d %d ",i,j);
}
if((m+1)&1) {
printf("%d\n",i);
}
else {
printf("\n");
}
flag=1;
break;
}
}
if(flag) {
break;
}
}
if(flag) {
continue;
}
if(m&1) {
printf("YES\n");
for(int i=1;i<=m;i+=2) {
printf("1 2 ");
}
cout<<endl;
continue;
}
int a,b,c;
bool fa=0,fb=0,f=0;
for(int i=1;i<=n;i++) {
fa=fb=0;
for(int j=1;j<=n;j++) {
if(ch[i][j]=='a') {
fa=1;
a=j;
}
if(ch[j][i]=='a') {
fb=1;
b=j;
}
}
if(fa&&fb) {
c=i;
f=1;
break;
}
}
if(!f) {
printf("NO\n");
continue;
}
printf("YES\n");
if(m%4==0) {
for(int i=0;i+4<=m;i+=4) {
printf("%d %d %d %d ",c,b,c,a);
}
printf("%d\n",c);
}
else {
for(int i=0;i+4<=m;i+=4) {
printf("%d %d %d %d ",b,c,a,c);
}
printf("%d %d %d\n",b,c,a);
}
}
return 0;
}
E. Sorting Books
这个官方题解只讲了转移方程,根本没讲原理,这里全部重新做个解释。
我们先考虑答案的范围。如果我们贪心,那么最多操作次数为 \(n\) 次,且一本书最多会被移动一次。
定状态
我们令 \(l_i,r_i\) 分别为第 \(i\) 种颜色从左往右数最早出现/最晚出现的位置。令 \(f_i\) 为在最后将所有书归好类后,\([i,n]\) 内最多有多少本书无需移动。明显,我们需要倒序枚举。最后的答案为 \(n-f_1\)。
我们记 \(tot_{i,j}\) 为在 \([j,n]\) 中,颜色为 \(i\) 的书本有多少本。
列状态转移方程
- 首先我们考虑的是 \(i\) 这本书要移动,那么此时最多可以保留不动的就是 \(f_{i+1}\) 本。
- 如果 \(i\) 这本书不移动,那么显然颜色为 \(a_i\) 的书都不要动,即 \(tot_{a_i,i}\) 本。那为什么在 \(i\neq l_{a_i}\),不加上 \(f_{r_{a_i}+1}\) 呢?我们可以重点关注一下样例:
5
1 2 2 1 3
若加上了,我们得到的 \(f\) 数组为 \(4,4,3,2,1\)(下标从 \(1\) 开始)。明显是错误的,应该为 \(3\)。为什么会错呢?我们来具体分析发生了甚么。
从本质出发,为什么可以保持颜色为 \(a_i\) 的书不移动,就是因为把 \([i,r_{a_i}]\) 中颜色不为 \(a_i\) 的全部移走。如果过早地进行了与有区间的合并,可能就会有两个区间有部分重叠。只有等所有颜色为 \(a_i\) 的数都出现过了,才可以进行区间的合并。
那上面那个样例说事,我们来理清关系:
- \(f_1=f_2\)
- \(f_2=f_4+1\)
- \(f_4=f_5+1\)。
好,到这里,就出现了问题。我们已经将 \([4,4],[5,5]\) 合并为了 \([4,5]\)。而在 \([2,3]\) 出现后,我们又进行了合并,有区间 \([2,5]\)。说明我们不可能将 \(2\) 移走了。我饿么您此时为了做出最优决策,只能将第一个 \(1\) 移走。明显是错误的。因为在 \([1,4]\) 区间可以被计算时,\([4,4]\) 已经“名花有主”了。
边界&初值
无。好干脆啊。
//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int MAXN=5e5+10;
int n;
int a[MAXN],l[MAXN],r[MAXN],f[MAXN],tot[MAXN];
signed main() {
cin>>n;
for(int i=1;i<=n;i++) {
a[i]=read();
if(!l[a[i]]) {
l[a[i]]=i;
}
}
for(int i=n;i;i--) {
if(!r[a[i]]) {
r[a[i]]=i;
}
}
for(int i=n;i;i--) {
tot[a[i]]++;
if(i==l[a[i]]) {
f[i]=max(tot[a[i]]+f[r[a[i]]+1],f[i+1]);
}
else {
f[i]=max(f[i+1],tot[a[i]]);//正确
// f[i]=max(tot[a[i]]+f[r[a[i]]+1],f[i+1];//错误
}
}
cout<<n-f[1]<<endl;
return 0;
}
F. AB tree
怎么又是 DP?这个官方题解很多不严谨的地方,我会一一纠正。
这个题是真的毒瘤。
首先我们考虑答案的最小值。若根节点的深度为 \(1\),深度最大的节点为 \(dm\),深度为 \(dmax\)。那么答案最小为 \(dmax\)。因为对于 \(1->dm\) 的路径上就会有 \(dmax\) 个不同的字符串。只要我们保证所有深度相同的节点字符都一样,就可以达到答案的最小值 \(dmax\)。
但是我们还需要满足 字符 a 的个数限制。我们令其有 \(a\) 个。显然我们要做一个背包,来确定是否可以做到在同一深度的点染成一个字符。时复杂度为 \(O(n^2)\)。显然,我们需要优化。
我们令深度为 \(i\) 的点有 \(sz_i\) 个。我们可以把 \(sz_i\) 相同的深度合并到一起,做多重背包。那么最多有多少个不同的 \(sz_i\) 呢?官方题解给出的数量是 \(O(\sqrt n)\)。很容易举出返利:\(23=1+2+3+4+5+6+2\)。那么真正的数量为多少呢?我们设数量为 \(x\)。为了使得 \(x\) 最大,不同的 \(x\) 个数一定是 \(1,2,3,\cdots ,x\)。解不等式组:
解集为 \(0\leq x\leq \frac{-1+\sqrt{8n+1}}{2}\)。我们可以粗略地认为 \(0\leq x\leq \sqrt{2n}\)。所以 \(x\) 最大为 \(\sqrt{2n}\)。
我们言归正传,如何 DP 呢?用二进制优化肯定超时了。单调队列优化应该是可以的,但是不利于我们后面构造方案。我们只能采取另一种方式。
基础多重背包
我们回顾一下最基础的做法。
定状态
先解决一些基本的定义,定义第 \(i\) 个物品最多可选 \(tot_i\) 个,所占空间为 \(val_i\)。共有 \(m\) 个物品。
令 \(f_{i,j}\) 表示考虑到前 \(i\) 个物品,是否存在总体积为 \(j\) 的方案。
转移方程
若存在 \(k\),满足 \(0\leq k\cdot val_i\leq j\),且 \(f_{i-1,j-k\cdot val_i}=\operatorname{true}\),则 \(f_{i,j}=\operatorname{true}\)。
否则 \(f_{i,j}=\operatorname{false}\)。
边界&&初值
\(f_{0,0}=\operatorname{true}\)。
很显然这个背包肯定超时,怎么优化呢?我们发现这里和普通被白哦不同的是我们只需要知道是否存在这种方案,而不需要求出一个最大值。这就是突破口。
优化后的背包算法
我们可以定义 \(k_{i,j}\),表示对于 \(f_{i,j}\),最小的满足条件的 \(k\)。(\(k\) 的定义同上。)
很显然,\(k_{i,j}\) 也需要转移,转移方程很简单:
那么对应的 \(f_{i,j}\) 的转移就简单了很多,我们不用在额外枚举 \(k\) 了。
如果最后 \(f_{m,a}=\operatorname{ture}\),就说明我们可以做到答案为 \(dmax\)。利用 \(k\) 数组,倒序构造一下即可。
我们考虑剩下的情况。什么时候答案为 \(dmax+1\) 呢。我们可以想象。如果对于两个深度相同的点来说,如果他们两个染上了相同的字符,但是他们付清的前缀不同,这两个串一定也不同,而且这个不同会传导到他们的子孙节点上。因此为了做到答案为 \(dmax+1\),只能在叶子节点处有不同的字符。
我们考虑贪心。我们从深度为 \(1\) 的节点一直考虑到深度为 \(dmax\) 的点。设现在还有 \(m\) 割点未被染色,有 \(y\) 个 a 可用,\(sz_i\leq \max(y,m-y)\),那么就用一个字符覆盖这一层。
我们考虑是否在任何情况下都可以做到答案为 \(dmax+1\)。若这一层都是非叶节点,我们知道所有非叶节点都有至少一个儿子,那么他们的数量必然小于等于 \(\frac{m}{2}\),且 \(\frac{m}{2}\leq \max(y,m-y)\)。因此永远可以做到答案为 \(dmax+1\)。我们只需要按上面的步骤贪心计算即可。
接下来就是一些恶心人的地方了,正如你们所见,我一开被疯狂卡空间,原因是我开的 \(f,k\) 数组都开了 \(500*100000\)。后来我想到一个绝妙的解决方法。。。
我们可以只开 \(500*100000\) 的空间。我们想,到底 \(a\) 代表 a 的数量还是 b 的熟练干其实不重要,所以如果 \(a>\frac{n}{2}\),就让 \(a=n-a\),只是标记一下,最后换回来即可。
代码挺长,下标特别乱。
//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int MAXN=1e5+10,inf=1e9;
int n,cnt,m,a,dmax,b;
int h[MAXN],sz[MAXN],k[500][MAXN>>1],f[500][MAXN>>1],tot[500],d[500],index[MAXN],size[MAXN];
set<int> s;
char ans[MAXN];
vector<int> dep[MAXN],vec[MAXN];
bool rev;
struct edge {
int v,nxt;
}e[MAXN<<1];
void addedge(int u,int v) {
e[++cnt].v=v;
e[cnt].nxt=h[u];
h[u]=cnt;
}
void insert(int u,int v) {
addedge(u,v);
addedge(v,u);
}
void dfs(int u,int fa,int d) {
dmax=max(d,dmax);
dep[d].push_back(u);
size[u]=1;
for(int i=h[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=fa) {
dfs(v,u,d+1);
size[u]+=size[v];
//子树大小
}
}
}
bool cmp(int x,int y) {
return size[x]<size[y];
}
signed main() {
cin>>n>>a;
b=n-a;
if(a>b) {
swap(a,b);
rev=1;
}
for(int i=2;i<=n;i++) {
insert(i,read());
}
dfs(1,0,1);
for(int i=1;i<=n;i++) {
sz[i]=dep[i].size();
//深度为 i 的深度集合
if(!sz[i]) {
continue;
}
sort(dep[i].begin(),dep[i].end(),cmp);
vec[sz[i]].push_back(i);
//大小为 sz_i 的深度集合
if(s.find(sz[i])==s.end()) {
d[++m]=sz[i];
index[sz[i]]=m;
tot[m]++;
s.insert(sz[i]);
}
else {
tot[index[sz[i]]]++;
}
}
f[0][0]=1;
for(int i=1;i<=m;i++) {
fill(k[i],k[i]+n+1,-inf);
for(int j=0;j<=a;j++) {
if(f[i-1][j]) {
f[i][j]=1;
k[i][j]=0;
}
else {
if(j>=d[i])
k[i][j]=k[i][j-d[i]]+1;
if(k[i][j]>=0&&j>=k[i][j]*d[i]&&k[i][j]<=tot[i]) {
f[i][j]=f[i-1][j-k[i][j]*d[i]];
}
else {
f[i][j]=0;
k[i][j]=-inf;
}
}
}
}
if(f[m][a]) {
printf("%d\n",dmax);
for(int i=m;i;i--) {
for(int j=0;j<k[i][a];j++) {
for(int l=sz[vec[d[i]][j]]-1;l>=0;l--) {
ans[dep[vec[d[i]][j]][l]]='a';
}
}
a-=d[i]*k[i][a];
}
for(int i=1;i<=n;i++) {
if(ans[i]!='a') {
ans[i]='b';
}
}
if(!rev)
printf("%s\n",ans+1);
else {
for(int i=1;i<=n;i++) {
printf("%c",'a'+'b'-ans[i]);
}
}
}
else {
/*if(b==489) {
printf("henhenhenaAAAAAAA\n");
return 0;
}*/
printf("%d\n",dmax+1);
char x='a',y='b';
if(rev) {
swap(a,b);
}
for(int i=1;i<=n;i++) {
if(!sz[i]) {
break;
}
if(b>a) {
swap(x,y);
swap(a,b);
}
while(sz[i]&&a) {
ans[dep[i][sz[i]-1]]=x;
sz[i]--;
a--;
}
while(sz[i]&&b) {
ans[dep[i][sz[i]-1]]=y;
sz[i]--;
b--;
}
}
printf("%s\n",ans+1);
}
//fclose(stdin);
//fclose(stdout);
return 0;
}
/*
9 6
1 2 2 4 4 4 3 1
*/