莫队算法
基本莫队算法介绍
莫队算法是一个分块算法,是由某国家集训队大佬提出的一个算法,我们就用一道 SDOI2009 的题来引入吧。
HH的项链
大概概括一下题意就是我们给定一个长度为 \(n\) 的自然数数列 \(a_1,a_2,a_3......a_{n-1},a_n\)。有 \(q\) 次询问,每次给出 \(l,r\),我们需要回答在 \([l,r]\) 内有多少不同的数。其中,\(n\le 5\cdot 10^4,m\le 2\cdot 10^5,a_i\le 10^6\)(这是原数据的范围,洛谷上有所加强)。
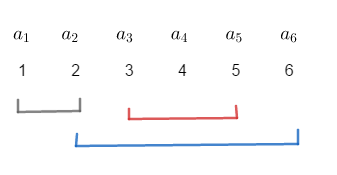
这就是题目的样例,那么我们知道,最暴力的方法就是对于每一次询问清空累加数组,每次都重新统计,时间复杂度为 \(O(q\cdot n)\)。
那么我们再加一个小优化,我们知道,对于第 \(2,3\) 次询问来说,他们有重复部分 \([3,5]\)。那么这个部分我们就不用重复处理,只需要加上 \([2,2],[6,6]\) 两个区间即可。
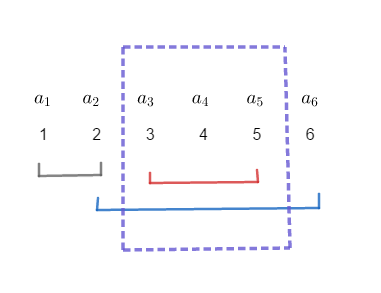
但是这样时间复杂度依然还是 \(O(q\cdot n)\)。我们如果造了这样一组数据,使得相邻两次的询问区间都没有交集,这样的时间复杂度反而还不如之前的暴力(指常数)。因此,我们一定需要一种较为稳定,且时间复杂度小的一种算法,也就是莫队。
众所周知,莫队是一个离线的算法。我们先对询问排序,这样可以让算法的时间复杂度大大退化,达到 \(O(q\cdot \sqrt{n}+ n\cdot \sqrt{n})\)。
莫队算法引用了分块的思想,我们定义:一个连续的数列称为一个块。 一个块的长度就是这个块所包含的数的个数。所以一个长度为 \(n\) 的数列可以分成至少 \(\lfloor\frac{n}{\lfloor \sqrt{n}\rfloor}\rfloor\) 个长度为 \(\lfloor \sqrt{n}\rfloor\) 的块,还有一个长度小于 \(\sqrt{n}\) 的块(这个块的长度可以为0)。注意我们接下来的讨论全部忽视这个小块,其涉及到的常数问题不讨论,且认为 \(\lfloor\frac{n}{\lfloor \sqrt{n}\rfloor}\rfloor=\sqrt{n}\)。 这会大大减少我的Latex公式编辑量。这样我们的时间复杂度和后续一些问题会比较好理解一些。毕竟这点误差还是在我们的接受范围内的。除非你要做 POJ 上的题,老爷机会让你崩溃的。
咳咳,我们回到正题。我们说一下排序的方式,然后再说一下为什么这样排序。我们先把数列分成 \(\sqrt{n}\) 个 长度为 \(\sqrt{n}\) 的块,如图。再说一遍:这里认为 \(\sqrt{n}=2\),但是这里有三个块,我们后面仍然认为只有 \(\sqrt{n}\) 块
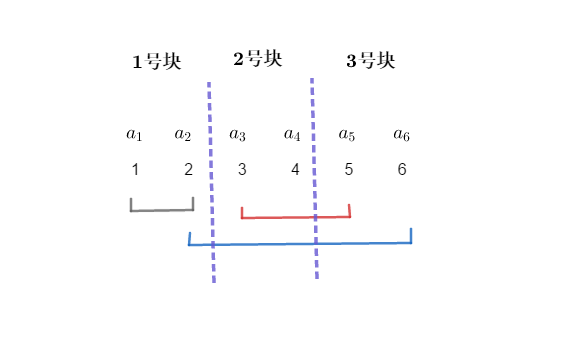
分好块了,我们现在说一下排序的细则:我们以询问区间的左端点 \(l\) 所在的块的编号为第一关键字,以右端点 \(r\) 的编号为第二关键字进行排序(注意有些人学的莫队是以右端点 \(r\) 所在的块的编号为第二关键字的,这个在部分情况下会有略微差别,一般认为是卡常,因为时间复杂度差别不是很大,本文中无说明情况下,以 \(r\) 的编号为第二关键字)。对样例进行完了排序后就是这样的一幅图:
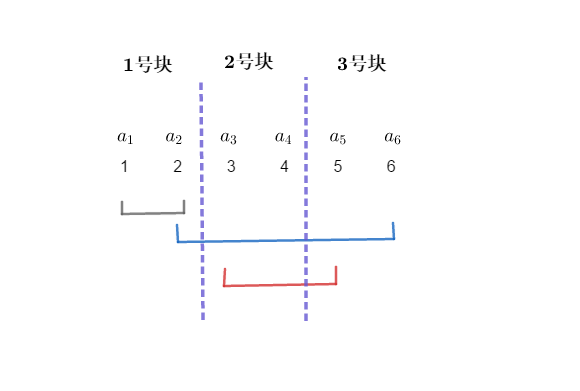
可能这个样例看着不是很明显优化在哪里,但是如果我们来推算一下时间复杂度,就知道这个算法的优点了。
我们首先考虑左端点的移动情况,由于我们排过序,所有在一个块内的移动最多 \(\sqrt{n}\),因为一个块的长度为 \(\sqrt{n}\)。如果是跨块的移动,可能为 \(n\),但这是unsustainable不可持续的,一旦移动到了下一个块中,就不会后移,所以跨块操作的平均情况应该是 \(\sqrt{n}\)。所以左端点的移动复杂度就为 \(O(q\sqrt{n})\)
我们再来看右端点,对于右端点来说,她是按编号排的序。所以对于左端点在于一个块中的询问来说,右端点的极端情况是从 \(1\) 一直移动到 \(n\)。我们总共有 \(\sqrt{n}\) 个块,所以与端点的比较好估算,是 \(O(n\sqrt{n})\)。
所以莫队算法的总时间复杂度就是 \(O(n\sqrt{n}+q\sqrt{n})\),可以通过此题。但由于洛谷上此题数据有所加强,无法使用莫队通过,需要用树状数组的方法来做,这里不再赘述这个问题。莫队的代码见下:
想要测这道题的同学可以到这里来测试
#include <bits/stdc++.h>
using namespace std;
const int maxn=5e4+10;
struct pr {
int l,r,id,bel;
}q[maxn*20];
int ans[maxn*20],a[maxn*20],n,q,num[1000010],cur;
bool cmp(pr x,pr y) {
if(x.bel!=y.bel) {
return x.bel<y.bel;
}
return x.r<y.r;
}
void add(int x) {
num[x] ++;
if (num[x] == 1)
cur ++;
}
void del(int x) {
num[x] --;
if (num[x] == 0)
cur --;
}
int main() {
cin >> n;
int blocks = sqrt(n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
cin >> q;
for (int i = 1; i <= q; ++i) {
q[i].id = i;
scanf("%d %d", &q[i].l, &q[i].r);
q[i].bel = (q[i].l - 1) / blocks + 1;//计算左端点所在的块
}
sort(q + 1, q + q + 1, cmp);
int l = 1, r = 0;
for (int i = 1; i <= q; ++i) {
while (l < q[i].l) del(a[l++]);//这些是 l,r 的移动
while (l > q[i].l) add(a[--l]);
while (r < q[i].r) add(a[++r]);
while (r > q[i].r) del(a[r--]);
ans[q[i].id] = cur;//统计情况;
}
for (int i =1 ; i <= q; ++i) {
printf("%d\n",ans[i]);
}
return 0;
}
但可能小伙伴们还有一些问题,比如说一下两个最有代表性:
Q1: 为什么选取块的长度为 \(\sqrt{n}\)?
A1: 解答这个问题,我们要先搞清一点,\(q\sqrt{n},n\sqrt{n}\) 中的 \(\sqrt{n}\) 含义不同。一个是块长,一个是块的个数。我们现在设块长为 \(k\)。那么时间复杂度为 \(O(qk+n\cdot \frac{n}{k})\)。可以用基本不等式得到:\(qk+n\cdot \frac{n}{k}\geq 2\sqrt{qn^2}\),也可以知道当 \(qk=n\cdot \frac{n}{k}\) 时,即 \(k=\frac{n\sqrt{q}}{q}\) 时,可以取到最小值 \(2\sqrt{qn^2}\)。所以最理想的块长为 \(\frac{n\sqrt{q}}{q} \approx \sqrt{n}\),时间复杂度最小为 \(2\sqrt{qn^2}\approx n\sqrt{n}+q\sqrt{n}\)。
我们可以来测一下这两种的区别:
\(\sqrt{n}\) 版:

\(\frac{n\sqrt{q}}{q}\) 版:

可见没什么大区别。所以我们一般采取长度为 \(\sqrt{n}\) 的块即可。
Q2: 为什么要分块,为何不能以左端点的编号为第一关键字?
A2: 我们可以这样想,以左端点为第一关键字的话,相当于块的长度 \(k=1\)。根据上面的推导知道这样时间复杂度是 \(O(q+n^2)\)。所以不可以的。
[国家集训队]小Z的袜子
那么我们再来看这样一道题。这道题明显是上一题的一个变形,只是我们要把上面的 \(\operatorname{add},\operatorname{del}\) 函数稍做调整。\(\operatorname{add}\) 就是把目前相同袜子颜色对答案贡献加上,把原来的减掉,\(\operatorname{del}\) 也一样。我们就可以得到以下代码:
void add(int x) {
cur-=num[x]*(num[x]-1);
num[x] ++;
cur+=num[x]*(num[x]-1);
}
void del(int x) {
cur-=num[x]*(num[x]-1);
num[x] --;
cur+=num[x]*(num[x]-1);
}
注意分数要约分即可。
带修莫队
莫队这种算法,一定会有修改呀。如果我们在查询的时候有修改,怎么办呢?我们的询问顺序打乱了,怎么处理修改呢?
[国家集训队]数颜色
我们还是以一道例题引入。题目自己看一看,我把样例的图放上来,具体就不解释了:
注意,我们这里改一改原来题目中的字母,在代码中不改。我们定义有 \(k\) 次操作,有 \(m\) 个修改操作,有 \(q\) 个询问操作。所以有 \(m+q=k\)。
其实我们很容易想到,我们记录一下每次询问前有多少次修改操作,因为我们不改变修改的顺序,这样,我们每次还要记录一下当前维护的区间进行了几次修改,然后我们只需要根据这些信息,可以把已进行的修改改回去,或者再继续改下去。
这道题洛谷的数据有所加强,原数据评测请到这里
慢着,这样就可以了吗?这样可以通过原数据,但是在洛谷上加强的数据无法通过。所以我们要想办法继续优化我们的算法。我们先来算一算时间复杂度。
左端点和右端点的移动仍然相同。我们算一下修改的时间复杂度。我们完全可以设计一种数据,先进行 \(\frac{q}{2}\) 次询问,然后集中进行 \(m\) 次修改,最后在把之前的询问再问一遍,这样你每次就要来回的修改,时间复杂度为 \(O(qm)\)。总时间复杂度为 \(O(q\sqrt{n}+n\sqrt{n}+qm)\)。更极限情况下,\(q=m=\frac{n}{2}\)。这样时间复杂度为 \(O(\frac{3\cdot n\sqrt{n}}{2}+\frac{n^2}{4})\)。显然炸掉。
我们的已解决办法就是来改一下块长,故技重施。我们还是取最极端的情况 \(q=m=\frac{n}{2}\)。此时设块长为 \(l\)(\(k\) 已经有意义了,所以换一个参数),最好的 \(l=\sqrt[3]{n^2}\)。这样就可以通过此题。另外,此题最好以右端点 \(r\) 所在块为第二关键字。这样在本题中发挥更好。(最后就是要加上一个火车头,开个 O2 才能通过)。
#pragma GCC diagnostic error "-std=c++11"
#pragma GCC target("avx")
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")//壮观
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int maxn=133334;
struct query {
int l,r,id,bell,belr,num;
}q[maxn];
struct modify {
int x,val,pre;
}c[maxn];
bool cmp(query x,query y) {
if(x.bell!=y.bell) {
return x.bell<y.bell;
}
if(x.belr!=y.belr)
return x.belr<y.belr;
return x.num<y.num;
}
int n,ans[maxn],m,a[maxn],cur,b[maxn],num[1000010];
void add(int x) {
num[x]++;
if(num[x]==1) {
cur++;
}
}
void del(int x){
num[x]--;
if(num[x]==0) {
cur--;
}
}
signed main() {
n=read();m=read();
int block=pow(n,2.0/3),mnum=0,cntq=0,cntm=0;
fill(ans,ans+1+m,-1);
for(int i=1;i<=n;i++) {
a[i]=read();
b[i]=a[i];
}
for(int i=1;i<=m;i++) {
char s;
cin>>s;
if(s=='Q') {
q[++cntq].l=read();
q[cntq].r=read();
q[cntq].bell=(q[cntq].l-1)/block+1;
q[cntq].belr=(q[cntq].r-1)/block+1;
q[cntq].id=i;
q[cntq].num=mnum;
}
else {
c[++cntm].x=read();
c[cntm].val=read();
c[cntm].pre=b[c[cntm].x];
b[c[cntm].x]=c[cntm].val;
mnum++;
}
}
int l=1,r=0,ch=0;
sort(q+1,q+cntq+1,cmp);
for(int i=1;i<=cntq;i++) {
while(l<q[i].l) del(a[l++]);
while(l>q[i].l) add(a[--l]);
while(r<q[i].r) add(a[++r]);
while(r>q[i].r) del(a[r--]);
while(ch>q[i].num) {
if(c[ch].x>=l&&c[ch].x<=r) {
del(c[ch].val);
add(c[ch].pre);
}
a[c[ch].x]=c[ch].pre;
ch--;
}
while(ch<q[i].num) {
ch++;
a[c[ch].x]=c[ch].val;
if(c[ch].x>=l&&c[ch].x<=r) {
del(c[ch].pre);
add(c[ch].val);
}
}
ans[q[i].id]=cur;
}
for(int i=1;i<=m;i++) {
if(ans[i]!=-1) {
printf("%lld\n",ans[i]);
}
}
return 0;
}