算法分析-快速排序QUICK-SORT

设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

一趟快速排序的算法是：

1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；

2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；

3）从j开始向前搜索，即由后开始向前搜索(j--)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；

4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；

5）重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）。

示例

假设用户输入了如下数组：

下标	0	1	2	3	4	5
数据	6	2	7	3	8	9

创建变量i=0（指向第一个数据）, j=5(指向最后一个数据), k=6(赋值为第一个数据的值)。

我们要把所有比k小的数移动到k的左面，所以我们可以开始寻找比6小的数，从j开始，从右往左找，不断递减变量j的值，我们找到第一个下标3的数据比6小，于是把数据3移到下标0的位置，把下标0的数据6移到下标3，完成第一次比较：

下标	0	1	2	3	4	5
数据	3	2	7	6	8	9

i=0 j=3 k=6

接着，开始第二次比较，这次要变成找比k大的了，而且要从前往后找了。递加变量i，发现下标2的数据是第一个比k大的，于是用下标2的数据7和j指向的下标3的数据的6做交换，数据状态变成下表：

下标	0	1	2	3	4	5
数据	3	2	6	7	8	9

i=2 j=3 k=6

称上面两次比较为一个循环。

接着，再递减变量j，不断重复进行上面的循环比较。

在本例中，我们进行一次循环，就发现i和j“碰头”了：他们都指向了下标2。于是，第一遍比较结束。得到结果如下，凡是k(=6)左边的数都比它小，凡是k右边的数都比它大：

下标	0	1	2	3	4	5
数据	3	2	6	7	8	9

如果i和j没有碰头的话，就递加i找大的，还没有，就再递减j找小的，如此反复，不断循环。注意判断和寻找是同时进行的。

然后，对k两边的数据，再分组分别进行上述的过程，直到不能再分组为止。

注意：第一遍快速排序不会直接得到最终结果，只会把比k大和比k小的数分到k的两边。为了得到最后结果，需要再次对下标2两边的数组分别执行此步骤，然后再分解数组，直到数组不能再分解为止（只有一个数据），才能得到正确结果。

 

 

Array.prototype.partition = function (start, end) {
    var i = start; //首元素
    var j = end; //最后一个元素
    var key = this[i]; //设置标兵
    var temp;
    while (j > i) {  //随着j--和i++，必然会相遇，这时候当前小标两边都排好序了
        
        //注意，如果右边换过一次，跳出循环，再从左边开始找。
        while (j > i) {
            if (this[j] < key) {
                temp = this[j];
                this[j] = this[i];
                this[i] = temp;
                break;
            } else {
                --j;
            }
        }
        
        while (j > i) {
            if (this[i] > key) {
                temp = this[i];
                this[i] = this[j];
                this[j] = temp;

                break;
            }
            ++i;
        }

    }
    console.log(i);
    console.log(A);

    return i;
};

Array.prototype.QUICK_SORT = function (start, end) {
    if (end > start) {
        var q = this.partition(start, end);
        arguments.callee.call(this,start, q - 1);
        arguments.callee.call(this,q + 1, end);
    }
};

var A = [3, 3, 4, 2,6,3,7,21,734,3265,2,4,60,0];
console.log(A);
A.QUICK_SORT(0, A.length-1);

下面给出算法导论里的伪代码，它的伪代码其实更加优秀：修改的只是partition部分。

先给出伪代码和过程：

 

 

 

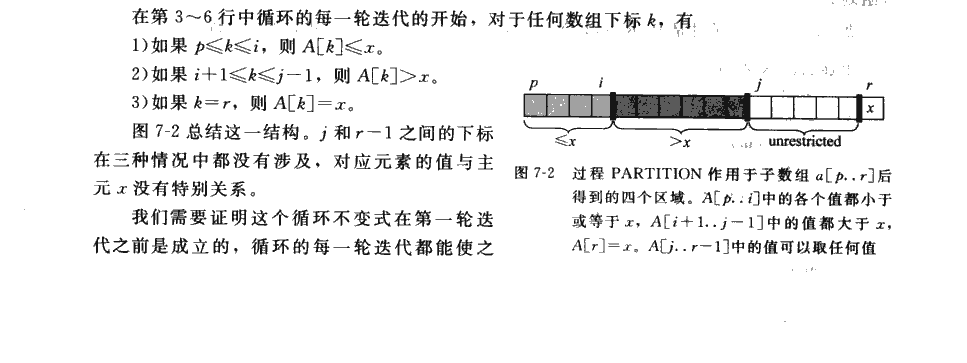
下面给出实现代码：

Array.prototype.partition = function (p, r) {
    var x = this[r];
    var i = p - 1;

    for (var j = p; j < r; j++) {
        if (this[j] <= x) {
            i++;
            this.swap(i, j);
        }
    }
    this.swap(i + 1, r);
    return i + 1;
};

Array.prototype.swap = function (i, j) {
    var temp = this[i];
    this[i] = this[j];
    this[j] = temp;
};

Array.prototype.QUICK_SORT = function (p, r) {
    if (r > p) {
        var q = this.partition(p, r);
        arguments.callee.call(this, p, q - 1);
        arguments.callee.call(this, q + 1, r);
    }
};

var A = [3, 3, 4, 2, 6, 3, 7, 21, 734, 3265, 2, 4, 60, 0];
console.log(A);
A.QUICK_SORT(0, A.length - 1);
console.log(A);

这个代码的优势很明显：首先不需要考虑越界了，然后就是循环少了。

 下面来探讨它的性能问题：

 我们用代换法来证明T(n) = T(n-1)+ T(0) + theta(n) = T(n-1) + theta(n);  T(n) = T(n - 1) + theta(n) = theta(n) + theta(n-1) + ... + theta(1) = theta(n^2)

思考：

当数组A的所有元素都具有相同值时，QUICKSORT的时间复杂度是什么？  

 分析：

当数组A所有元素相同时，QUICKSORT中的划分时极为不平衡的,n-1:0的划分,T(n)=T(n-1)+Θ(n)解这个递归式T(n)=Θ(n^2) 

 思考：

银行经常会按照交易时间，来记录某一账户的交易情况。但是，很多人却喜欢收到银行对账单是按照支票号码的顺序来排列的。这是因为，人们通常  都是按照支票号码的顺序来开出支票的，而商人也通常都是根据支票编号的顺序兑付支票。这一问题时按照交易时间排序的序列转换成按支票号排序的序列，它是指上是一个对几乎有序的输入序列进行排序的问题。请证明：在这个问题上，INSERTION-SORT的性能往往要优于QUICKSORT？

分析：

插入排序在基本有序的情况下，基本无需移动任何元素来插入，所以只有外层循环了n次，所以时间复杂度为O(n)

 快速排序在基本有序的情况下，在划分数组时，划分得非常不平衡，那么其时间复杂度是O(nlgn),而达到完全有序时，时间 复杂度达到O(n^2)，所以总之插入排序要优于快速排序。 

思考：

假设快速排序的每一层所做的划分的比例都是1-a:a，其中0<a<=1/2且是一个常数。是证明，在相应的递归树中，叶结点的最小深度大约是  -lgn/lga,最大深度大约是-lgn/lg(1-a)(无需考虑整数舍入问题) 

分析：

最小深度为每次划分后都是选择最小的一部分继续往下走，每次乘以a。一次迭代减少的元素数从n到an，迭代m次直到剩下的元素为1。

则(a^m)*n = 1， a^m = 1/n，取对数得mlga = -lgn，m = -lgn/lga。

同理可得((1-a)^M)*n = 1，M = -lgn/lg(1-a)。

思考：

试证明：在一个随机输入数组上，对于任何常数0<a<=1/2，PARTITION产生比1-a:a更平衡的划分的概率约为1-2a      

证明：

则X+Y=n  那么根据书上根据平衡的定义，X-Y差值越大，比例就越高，那么越不平衡，只有X-Y差值越小，越接近0，X约等于Y的时候  越平衡。

 分三种情况讨论：1）当X/n<a时，那么Y/n>1-a, |X-Y|/n>1-2a>0               

                              2）当X/n>1-a时，那么Y<a, |X-Y|/n>1-2a>0         

                              3）当a<X/n<1-a时，那么a<Y<1-a,0<|X-Y|/n<1-2a

 只有当|X-Y|/n距离小于一个数时，才可能X-Y差值趋向于0,划分的就越平衡。所以我们选择情况3的这种划分。  在an与(1-a)n之间取X的值，因为划分X落在区间[0,n]上是等可能性的，所以符合均匀分布，落在[an,(1-a)n}]上的任意一点  的概率也是等可能的，所以P{an≤x≤(1-a)n}=((1-a)n-an)/(n-0)=1-2a。得证！ 

思考：为什么我们分析随机化算法的期望运行时间，而不是其最坏运行时间呢？

 分析：随机化算法不能改变最坏情况下得运行时间，但是能降低最坏情况发生的概率。

思考：

在RANDOMIZED-QUICKSORT的运行过程中，在最坏情况下，随机数生成器RANDOM被调用了多少次？在最好情况下呢？ 

 分析：

最好情况是均匀划分，其时间复杂度 T(n)=2T(n/2)+1 =>主定理case1得T(n)=Θ(n)   

最坏情况是分成不平衡的划分，其时间复杂度 T(n)=T(n-1)+T(0)+1 各式相加得=>T(n)=Θ(n)