










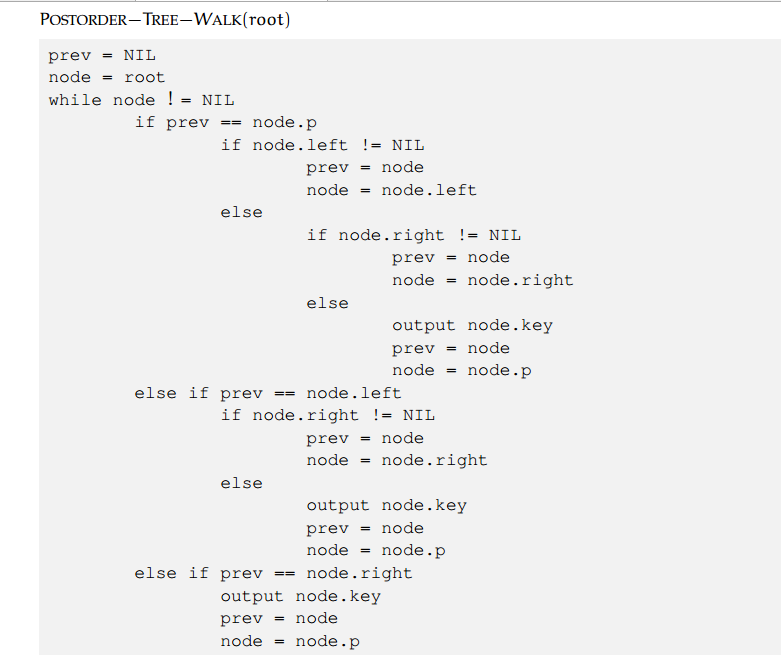
前序遍历:


后序遍历:







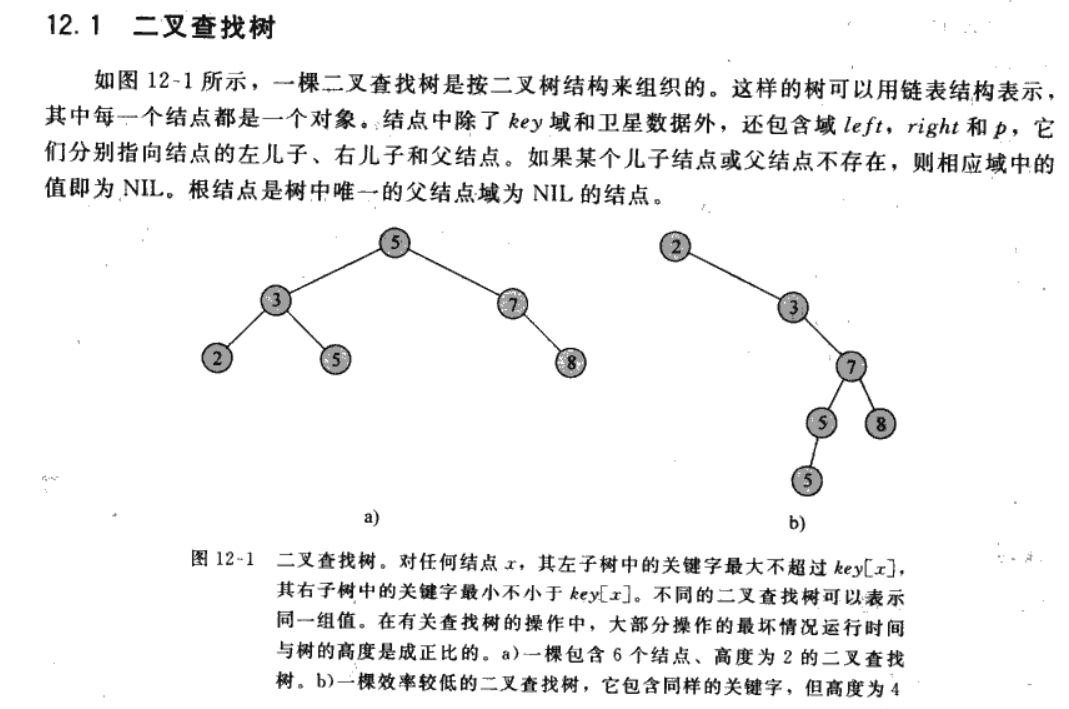
二叉查找树按照二叉树进行组织。二叉查找树关键字的存储方式总是瞒住二叉查找树性质:
设x为二查查找树种一个节点。如果y是x的左子树中的一个节点,那么key[x] >= key[y]。如果y是x的右子树的一个节点,那么key[x] <= key[y]。
这样对二叉查找树进行中序遍历就可得到书中所有元素的一个非降序排列。
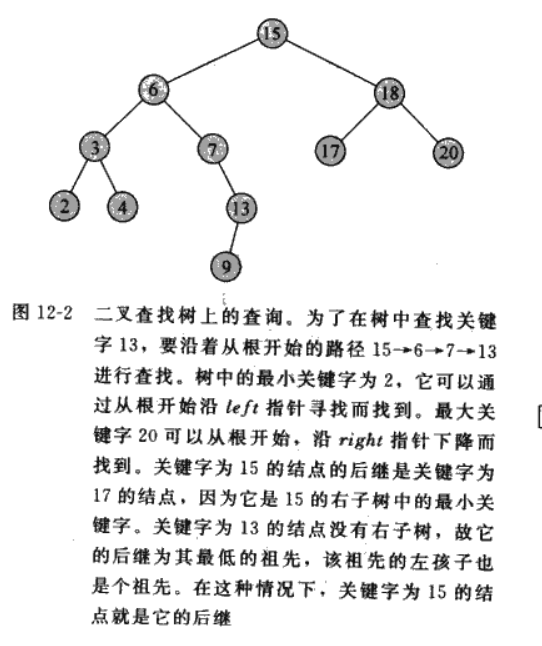
查找某一个存在节点的前驱和后继。某一个节点x的后继就是大于key[x]的关键字中最小的那个节点,前驱就是小于key[x]的关键字中最大的那个节点。查找二叉前驱和后继节点的算法如下所示:
1 typedef struct _node { 2 struct _node *left_child; 3 struct _node *right_child; 4 struct _node * parent; 5 ctype data; 6 }node; //树节点数据结构定义 7 8 typedef node* Tree; 9 10 //查找二叉查找树中关键字最小的节点,返回指向该节点的指针 11 Tree tree_minimum(Tree root) 12 { 13 Tree p = root; 14 while (p->left_child != null) 15 p = p->left_child; 16 return p; 17 } 18 19 //查找二叉查找树中关键字最大的节点,返回指向该节点的指针 20 Tree tree_maxmum(Tree root) 21 { 22 Tree p = root; 23 24 while (p->right_child != null) 25 { 26 p = p->right_child; 27 } 28 return p; 29 } 30 31 //查找二叉查找树中节点x的后继节点,返回指向该节点的指针 32 //在查找过程中,如果节点x右子树不为空,那么返回右子树的最小节点即可 33 //如果节点x的右子树为空,那么后继节点为x的某一个祖先节点的父节点,而且该祖先节点是作为其父节点的左儿子 34 Tree tree_successor(Tree x) 35 { 36 if (x->right_child != null) 37 return tree_minimum(x->right_child); 38 39 //x用来保存待确定的节点 40 //y为x的父节点 41 Tree y = x->parent; 42 43 while (y != NULL && x == y->right_child) 44 { 45 x = y; 46 y = y->parent; 47 } 48 return y; 49 } 50 51 52 //查找二叉查找树中节点x的前驱节点,返回指向该节点的指针 53 //在查找过程中,如果节点x左子树不为空,那么返回左子树的最大节点即可 54 //如果节点x的左子树为空,那么前驱节点为x的某一个祖先节点的父节点,而且该祖先节点是作为其父节点的右儿子 55 Tree tree_predecessor(Tree x) 56 { 57 if (x->left_child != null) 58 return tree_maxmum(x->left_child); 59 60 Tree y = x->parent; 61 while (y != NULL && x == y->left_child) 62 { 63 x = y; 64 y = y->parent; 65 } 66 return y; 67 }






插入算法
首先执行查找算法,找出被插结点的父亲结点。
判断被插结点是其父亲结点的左、右儿子。将被插结点作为叶子结点插入。
若二叉树为空。则首先单独生成根结点。
注意:新插入的结点总是叶子结点。

1 struct BiTree { 2 int data; 3 BiTree *lchild; 4 BiTree *rchild; 5 }; 6 7 //在二叉排序树中插入查找关键字key 8 BiTree* InsertBST(BiTree *t,int key) 9 { 10 if (t == NULL) 11 { 12 t = new BiTree(); 13 t->lchild = t->rchild = NULL; 14 t->data = key; 15 return t; 16 } 17 18 if (key < t->data) 19 t->lchild = InsertBST(t->lchild, key); 20 else 21 t->rchild = InsertBST(t->rchild, key); 22 23 return t; 24 } 25 26 //n个数据在数组d中,tree为二叉排序树根 27 BiTree* CreateBiTree(BiTree *tree, int d[], int n) 28 { 29 for (int i = 0; i < n; i++) 30 tree = InsertBST(tree, d[i]); 31 return tree; 32 }
三、二叉搜索树的删除
对于二叉搜索树的删除操作,主要是要理解其中的几种情况,写起来还是比较简单的。
当然一开始还是需要判断要删除的节点是否存在于我们的树中,如果要删除的元素都不在树中,就直接返回false;否则,再分为以下四种情况来进行分析:
》要删除的节点无左右孩子
》要删除的节点只有左孩子
》要删除的节点只有右孩子
》要删除的节点有左、右孩子
删除方法解释:
对于第一种情况,我们完全可以把它归为第二或者第三种情况,就不用再单独写一部分代码进行处理;
》如果要删除的节点只有左孩子,那么就让该节点的父亲结点指向该节点的左孩子,然后删除该节点,返回true;
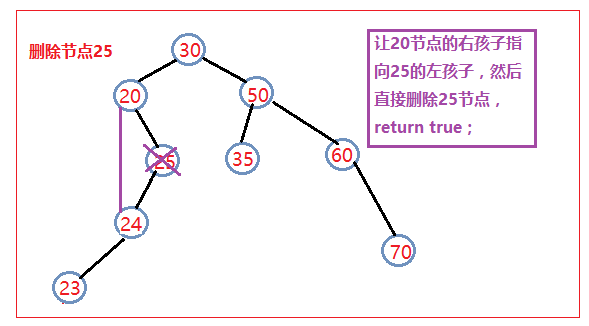
》如果要删除的节点只有右孩子,那么就让该节点的父亲结点指向该节点的右孩子,然后删除该节点,返回true;
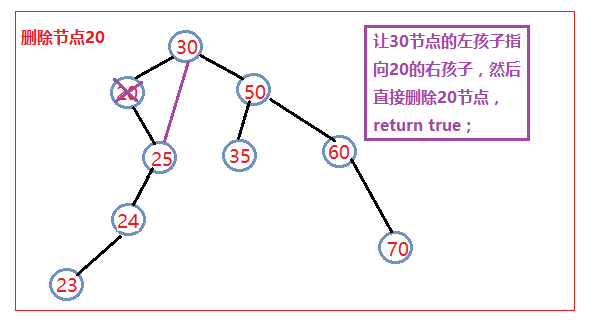
对于上面这两种情况我们还应该在之前进行一个判断,就是判断这个节点是否是根节点,如果是根节点的话,就直接让根节点指向这个节点的左孩子或右孩子,然后删除这个节点。
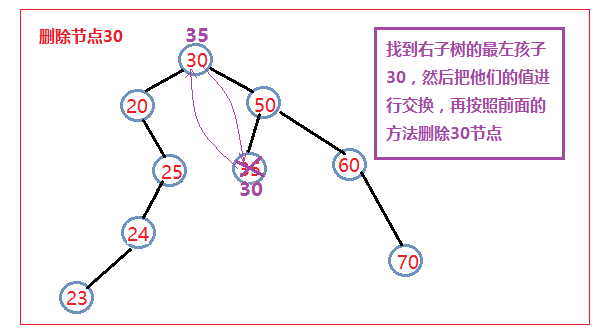
》最后一种也是最麻烦的一种就是要删除的节点的左右孩子都存在。此时我们的删除方法如下:
1、找到该节点的右子树中的最左孩子(也就是右子树中序遍历的第一个节点)
2、把它的值和要删除的节点的值进行交换
3、然后删除这个节点即相当于把我们想删除的节点删除了,返回true;
1 bool Remove(const K& key) 2 { 3 assert(_root); 4 Node* parent = NULL; 5 Node* pcur = _root; 6 Node* del = pcur; 7 while (pcur != NULL && pcur->_key != key) 8 { 9 if (pcur->_key > key) 10 { 11 parent = pcur; 12 pcur = pcur->_left; 13 } 14 else if (pcur->_key < key) 15 { 16 parent = pcur; 17 pcur = pcur->_right; 18 } 19 } 20 if (pcur == NULL) 21 return false; 22 if (pcur->_left == NULL) //只有右孩子 23 { 24 //如果pcur就是根节点的话,让根节点指向根的右 25 if (pcur == _root) 26 _root = pcur->_right; 27 else if (pcur == parent->_left) 28 { 29 parent->_left = pcur->_right; 30 } 31 else 32 { 33 parent->_right = pcur->_right; 34 } 35 del = pcur; 36 } 37 else if (pcur->_right == NULL) //只有左孩子 38 { 39 //如果是根节点,让根节点指向根的左 40 if (pcur == _root) 41 _root = pcur->_left; 42 else if (parent->_left == pcur) 43 { 44 parent->_left = pcur->_left; 45 } 46 else 47 parent->_right = pcur->_left; 48 del = pcur; 49 } 50 //pcur左右孩子都不为空 51 else 52 { 53 //找到节点右子树的最左节点 54 Node* left = pcur->_right; 55 parent = pcur; 56 while (left->_left) 57 { 58 parent=left; 59 left = left->_left; 60 } 61 del = left; 62 pcur->_key = left->_key; //交换节点的值 63 if (parent->_left == left) 64 { 65 parent->_left = left->_right; 66 } 67 else 68 { 69 parent->_right = left->_right; 70 } 71 72 } 73 delete del; 74 return true; 75 }
===================================================================