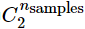一、分类
1、精确率
被识别成正类的,有多少是真正的正类。
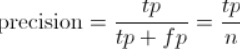
2、召回率
真正的正类,有多少等被找出来(召回)。
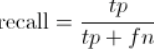
3、准确率
被分类样本总数中,有多少是正确分类的。
4、F1
F1 = 2 * (precision * recall) / (precision + recall)
5、平均精确率(AP)average precision
Precision-recall曲线以下面积
6、AUC(area under curve)
TP-FP曲线以下面积
二、回归
1、MSE(平均平方误差)

2、RMSE(平均平方根误差)
为MSE平方根
3、MAE(平均绝对值误差)

4、 R2 score
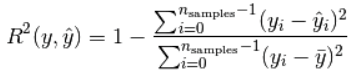
R2决定系数表达了模型多大程度解释了因变量的变化。
如果单纯用残差平方和等指标衡量模型效果会受到因变量的数量级的影响。例如:例如一个模型中的因变量:10000、20000…..,而另一个模型中因变量为1、2……,这两个模型中第一个模型的残差平方和可能会很大,而另一个会很小,但是这不能说明第一个模型就别第二个模型差。所以指标式中的分式的分母,相当于除掉了因变量的数量级。
5、可解释方差得分
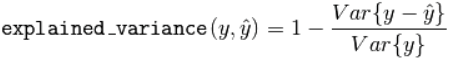
三、聚类
1、没有给定类别标签
1.1紧密度
计算每个类到其质心的平均距离,再计算所有类的平均距离的平均。越小越好。缺点:没有考虑类间距离。

1.2间隔性
计算各类质心两两之间的距离平均。越大越好。缺点:没有考虑类内距离凝聚性。
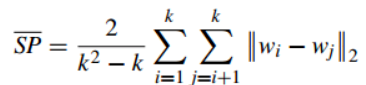
1.3Davies-Bouldin Index(戴维森堡丁指数)(分类适确性指标)(DB)(DBI)
任意两类别的类内距离平均距离(CP)之和除以两聚类中心距离最大值,然后求平均。缺点:因使用欧式距离,所以对于环状分布聚类评测很差。
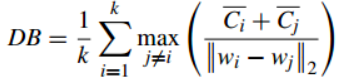
1.4Dunn Validity Index (邓恩指数)(DVI)
任意两个簇元素的最短距离(类间)除以任意簇中的最大距离(类内)。缺点:对离散点的聚类测评很高、对环状分布测评效果差
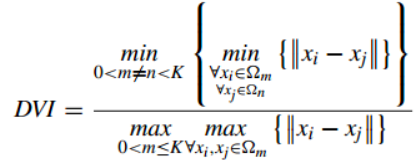
2、给定类别标签
2.1Cluster Accuracy (准确性)(CA)
聚类正确的百分比
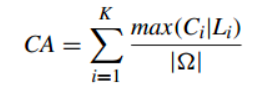
2.2Rand index(兰德指数)(RI) 、Adjusted Rand index(调整兰德指数)(ARI)

C表示实际类别信息,K表示聚类结果,a表示在C与K中都是同类别的元素对数,b表示在C与K中都是不同类别的元素对数
其中表示数据集中可以组成的对数,RI取值范围为[0,1],值越大意味着聚类结果与真实情况越吻合。
为了实现“在聚类结果随机产生的情况下,指标应该接近零”,调整兰德系数(Adjusted rand index)被提出,它具有更高的区分度:
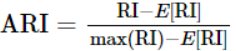
2.3Normalized Mutual Information (标准互信息)(NMI)、Mutual Information(互信息)(MI)
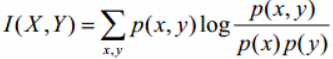
标准化互聚类信息都是用熵做分母将MI值调整到0与1之间,一个比较多见的实现是下面所示:

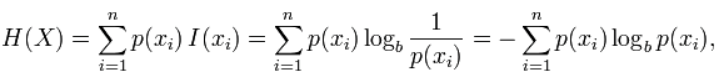
2.4同质性、完整性
我们假定数据集有N个数据。分类classes使用C=ci|i=1,…,n,聚类结果clusters,K= {ki|1,…,m }。 所以A = a{ij}中的aij表示数据属于class ci 和 clusterkj
同质性是指:每一个cluster(聚类结果簇)中所包含的数据应归属于一个class(类)。

完整性是指:所有属于同一个class的数据应该被归到相同的cluster中。

其中: