对于有顺序的数组的查询操作,首先想到二分
二分查找分三种情况:
- 寻找一个数(基本的二分搜索)
[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为3
返回 4
- 寻找左侧边界的二分搜索
[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回: 1(第一个2的索引)
- 寻找右侧边界的二分搜索
[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回: 3(最后一个2的索引)
1. 寻找一个数(基本的二分搜索)
- 查找的数不为重复元素
[1, 2, 2, 3, 4, 5, 6, 7] 查找元素为3
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
2. 寻找左侧边界的二分搜索
[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回: 1(第一个2的索引)
找到 target 时不要立即返回,而是缩小「搜索区间」的上界 right,在区间 [left, mid] 中继续搜索,即不断向左收缩,达到锁定左侧边界的目的。
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// 搜索区间为 [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
}
// 检查出界情况
if (left >= nums.length || nums[left] != target)
return -1;
return left;
}
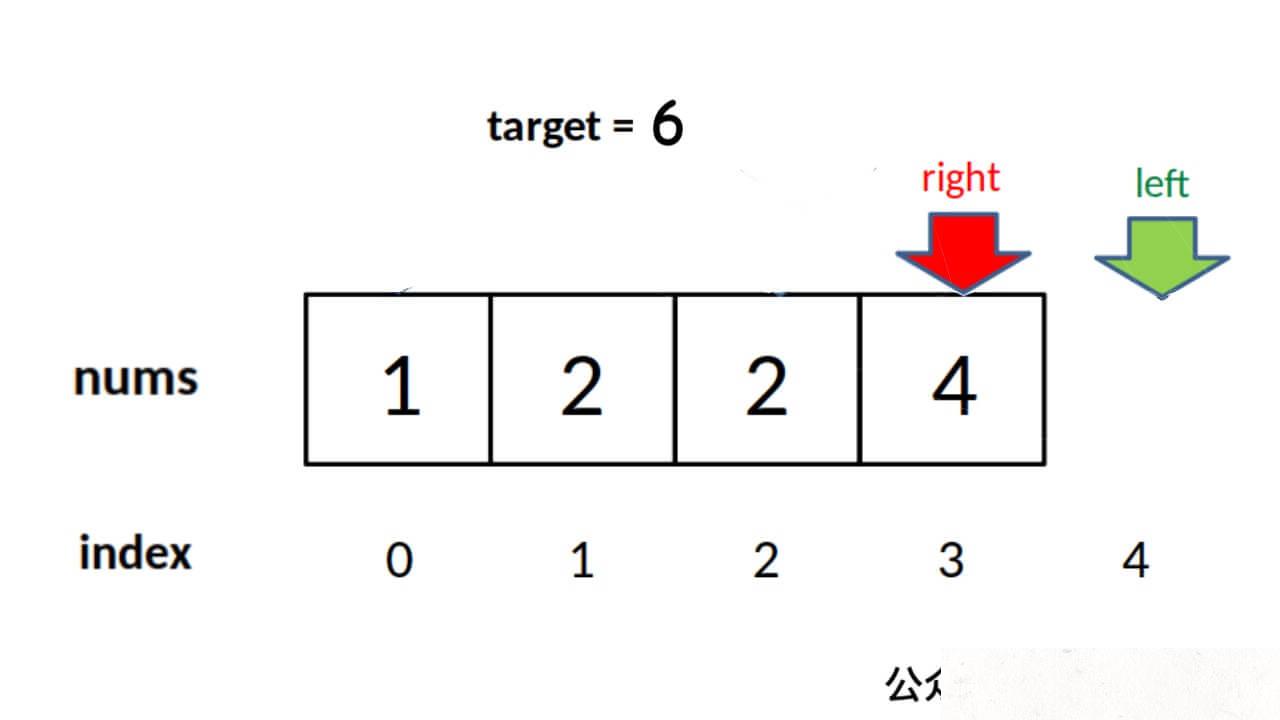
由于 while 的退出条件是 left == right + 1,所以当 target 比 nums 中所有元素都大时,会存在以下情况使得索引越界
因此,最后返回结果的代码应该检查越界情况
- 寻找右侧边界的二分搜索
[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回: 3(最后一个2的索引)
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 这里改成收缩左侧边界即可
left = mid + 1;
}
}
// 这里改为检查 right 越界的情况,见下图
if (right < 0 || nums[right] != target)
return -1;
return right;
}
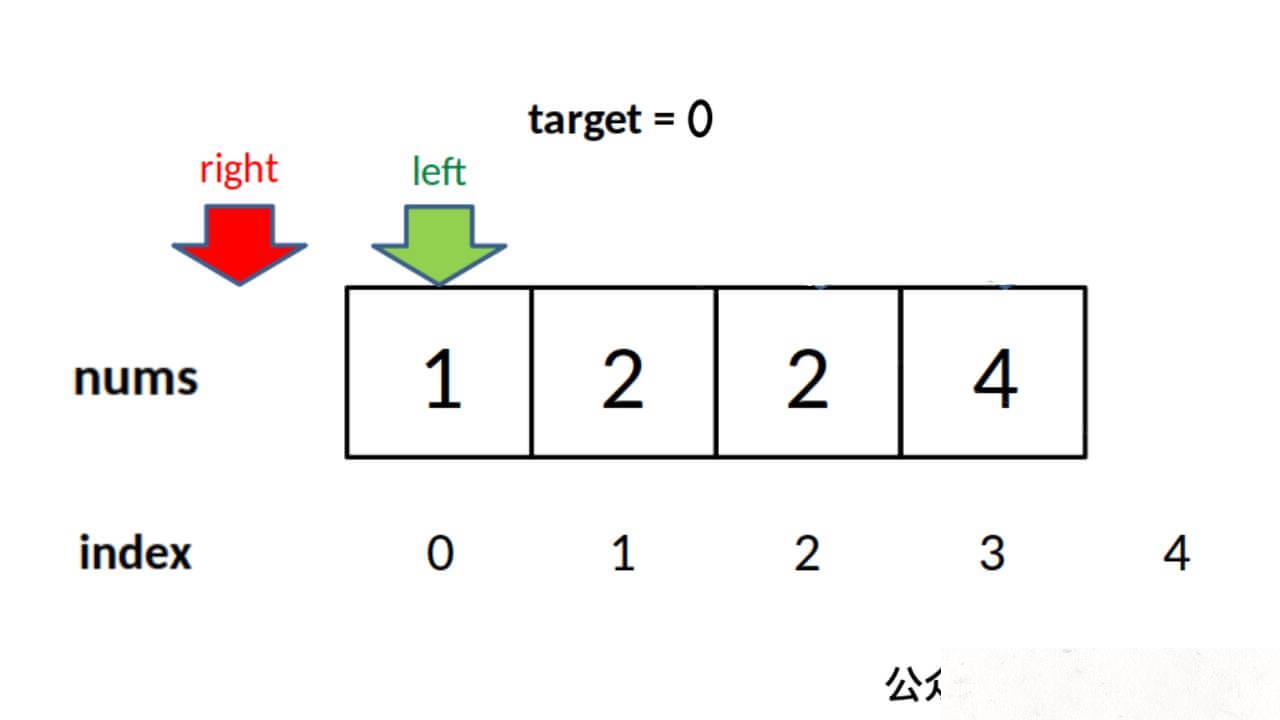
- 当 target 比所有元素都小时,right 会被减到 -1,所以需要在最后防止越界:
常见的二分查找的题
1、 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
- 0 <= nums.length <= 105
- -109 <= nums[i] <= 109
- nums 是一个非递减数组
- -109 <= target <= 109
题解:寻找左右边界的二分查找
- 如果数组为空,返回[-1, -1]
2.寻找目标值的左边界,并判断 l 的越界情况;
- 越界: 返回
- 不越界:将 l 添加到结果数组中
3.寻找目标值的右边界
- 由于步骤2中已经求出了左边界,故有边界一定存在,直接添加到res中
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] res = new int[]{-1, -1 };
int len = nums.length;
if(len == 0) return res ;
int l = 0, r = len - 1;
//寻找目标值的左边界
while(l <= r) {
int mid = l + (r - l) / 2;
if(nums[mid] >= target){
r = mid - 1;
}else{
l = mid + 1;
}
}
if(l >= len || nums[l] != target){
return res;
}else {
res[0] = l;
l = 0;
r = len - 1;
//寻找目标值的右边界
while(l <= r) {
int mid = l + (r - l) / 2;
if(nums[mid] <= target){
l = mid + 1;
}else{
r = mid - 1;
}
res[1] = r;
}
}
return res;
}
}
旋转数组的最小值
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
示例 1:
输入:[3,4,5,1,1,2]
输出:1
示例 2:
输入:[2,2,2,0,1]
输出:0
算法流程:
-
初始化: 声明 l, r 双指针分别指向 nums 数组左右两端;
-
循环二分: 设 m = l + (r - l) / 2为每次二分的中点,可分为以下三种情况:
(1)当 nums[m] > nums[r] 时: m 一定在 左排序数组 中,即旋转点 x 一定在 [m + 1, r] 闭区间内,因此执行 l = m + 1;
(2)当 nums[m] < nums[r] 时: m 一定在 右排序数组 中,即旋转点 x 一定在[l, m] 闭区间内,因此执行 r = m;
(3)当 nums[m] = nums[r] 时: 无法判断 m 在哪个排序数组中,即无法判断旋转点 x 在 [l, m] 还是 [m + 1, r] 区间中。解决方案: 执行 r = r - 1 缩小判断范围,分析见下文。
-
返回值: 当 l = r 时跳出二分循环,并返回 旋转点的值 nums[l]即可。
public class minNumInRotateArray {
public static void main(String[] args) {
int[] arrays = {4,4};
int res = solution(arrays);
System.out.println(res);
}
public static int solution(int[] arrays) {
int l = 0, r = arrays.length - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if(arrays[mid] > arrays[r]){
l = mid + 1;
}else if(arrays[mid] < arrays[r]){
r = mid;
}else {
r--;
}
}
return arrays[l];
}
}
33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5, ,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
- 1 <= nums.length <= 5000
- -10^4 <= nums[i] <= 10^4
- nums 中的每个值都 独一无二
- 题目数据保证 nums 在预先未知的某个下标上进行了旋转
- -10^4 <= target <= 10^4
public class minNumInRotateArray {
public static void main(String[] args) {
int[] arrays = {5,6,76,1,2,3,4};
int res = solution(arrays, 4);
System.out.println(res);
}
public static int solution(int[] arrays, int target) {
int l = 0, r = arrays.length - 1, mid = 0;
while (l <= r) {
mid = l + (r - l) / 2;
if (arrays[mid] == target) {
return mid;
}
// 先根据 nums[mid] 与 nums[lo] 的关系判断 mid 是在左段还是右段
if (arrays[mid] >= arrays[l]) {
// 再判断 target 是在 mid 的左边还是右边,从而调整左右边界 lo 和 hi
if (target >= arrays[l] && target < arrays[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (target > arrays[mid] && target <= arrays[r]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
}