POJ1456 Supermarket

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#define max(a, b) ((a) > (b) ? (a) : (b))

const int INF = 0x3f3f3f3f;
const int MAXN = 10000 + 10;
const int MAXP = 10000 + 10;

inline void read(int &x)
{
    x = 0;char ch = getchar(), c = ch;
    while(ch < '0' || ch > '9')c = ch, ch = getchar();
    while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar();
    if(c == '-') x = -x; 
}

int fa[MAXP], rank[MAXN], value[MAXN], t[MAXN], cnt[MAXN], n, ans, ma;

int find(int x)
{
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

bool cmp(int a, int b)
{
    return value[a] > value[b];
}

int main()
{
    while(scanf("%d", &n) != EOF)
    {
        ans = ma = 0;
        for(register int i = 1;i <= n;++ i)
            read(value[i]), read(t[i]), cnt[i] = i, ma = max(ma, t[i]);
        for(register int i = 1;i <= ma;++ i)
            fa[i] = i;
        std::sort(cnt + 1, cnt + 1 + n, cmp);
        register int p;
        for(register int i = 1;i <= n;++ i)
        {
            p = cnt[i];
            int tmp = find(t[p]);
            if(tmp != 0) ans += value[p], fa[tmp] = tmp - 1;
        }
        printf("%d
", ans);
    }
    return 0;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#define max(a, b) ((a) > (b) ? (a) : (b))

const int INF = 0x3f3f3f3f;
const int MAXN = 10000 + 10;
const int MAXP = 10000 + 10;

inline void read(int &x)
{
    x = 0;char ch = getchar(), c = ch;
    while(ch < '0' || ch > '9')c = ch, ch = getchar();
    while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar();
    if(c == '-') x = -x; 
}

int value[MAXN], t[MAXN], cnt[MAXN], n, ans, ma;

bool cmp(int a, int b)
{
    return t[a] > t[b];
} 

struct cmpp
{
    bool operator()(int a, int b)
    {
        return value[a] < value[b];
    }    
};

std::priority_queue<int, std::vector<int>, cmpp> q;

int main()
{
    while(scanf("%d", &n) != EOF)
    {
        while(q.size())q.pop();
        ans = ma = 0;
        for(register int i = 1;i <= n;++ i)
            read(value[i]), read(t[i]), cnt[i] = i;
        std::sort(cnt + 1, cnt + 1 + n, cmp);
        int p = 1;ma = t[cnt[1]];
        for(register int i = ma;i >= 1;-- i)
        {
            while(t[cnt[p]] == i)q.push(cnt[p]), ++p;
            if(q.size())ans += value[q.top()],q.pop();
        }
        printf("%d
", ans);
    } 
    return 0;
}

Supermarket

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 13387		Accepted: 6019

Description

A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σ_x∈Sellpx. An optimal selling schedule is a schedule with a maximum profit.
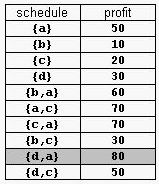
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.

Input

A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output

For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input

4  50 2  10 1   20 2   30 1

7  20 1   2 1   10 3  100 2   8 2
   5 20  50 10

Sample Output

80
185

Hint

The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.

Source

Southeastern Europe 2003

 

【题解】

　　贪心题目，都是优先买价值高的，需要保证时间合法。不难发现过期晚的可以在这个时间之前任意时刻买，所以时间一般降序处理。

　　做法一：可以降序枚举时间，把对应时间刚好马上就要过期但没过期的加入优先队列中，每个时间从优先队列取出价值最高的即可。正确性显然

       做法二：用并查集维护某个时间向前追溯到的第一个没有买东西的时间。然后按价值降序枚举物品，把他的时间p所代表的父亲t合并到t-1上，如果t是0代表不能选。正确性亦显然。

       标程见上房