【NOIp模拟赛】花

【问题描述】

商店里出售n种不同品种的花。为了装饰桌面，你打算买m支花回家。你觉得放两支一样的花很难看，因此每种品种的花最多买1支。求总共有几种不同的买花的方案？答案可能很大，输出答案mod p的值。

【输入格式】

一行3个整数n，m，p，意义如题所述。

【输出格式】

一个整数，表示买花的方案数。

【输入输出样例1】

flower.in	flower.out
4 2 5	1

         见选手目录下的flower /flower1.in与flower /flower1.out

 

【输入输出样例1说明】

    用数字1,2,3,4来表示花的种类的话，4种花里买各不相同的2支的方案有(1,2)、(1,3)、(1,4)、(2,3)、(2,4)、(3,4)，共6种方案，模5后余数是1。

【输入输出样例2】

         见选手目录下的flower /flower2.in与flower /flower2.out

【数据范围】

对于30%的数据，n,m≤10

对于50%的数据，n,m≤1000

对于80%的数据，1≤m≤n≤50,000

对于100%的数据，1≤m≤n≤1,000,000，p≤1,000,000,000

分析

30分，直接用组合数公式算。

50分，利用杨辉三角的递推式，在加的过程中取余。

100分，还是利用组合数的公式，在计算之前是可以约分的。在对分子分母进行质因数分解继续约分，最后可能要用到快速幂。

组合数公式

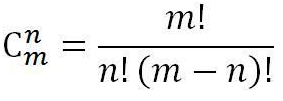
代码

50分代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1000+5;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
int n,m,p;
int c[maxn][maxn];
int main()
{
    freopen("flower.in","r",stdin);
    freopen("flower.out","w",stdout);
    n=read();m=read();p=read();
    c[1][0]=1; c[1][1]=1;
    for(int i=2;i<=n;i++)
    {
        c[i][0]=1;c[i][i]=1;
        for(int j=1;j<i;j++)
        c[i][j]=(c[i-1][j]%p+c[i-1][j-1]%p)%p;
    }
    printf("%d
",c[n][m]);
    return 0;
}

100代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1000000+5;
typedef long long ll;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
int n,m,p,tot;
int prime[maxn],cnt[maxn];
bool a[maxn];
ll ans=1;
void mkp()
{
    for(int i=2;i<=n;i++)
    {
        if(!a[i]) prime[++tot]=i;
        for(int j=1;j<=tot&&prime[j]*i<=n;j++)
        {
            a[prime[j]*i]=1;
            if(i%prime[j]==0) break;
        }
    }
}
void work1(int x)
{
    for(int i=1;i<=tot;i++)
    {
        while(x%prime[i]==0) 
        {
            cnt[prime[i]]++;
            x=x/prime[i];
        }
        if(x==1) break;
        if(!a[x])
        {
            cnt[x]++;
            break;
        }
    }
}
void work2(int x)
{
    for(int i=1;i<=tot;i++)
    {
        while(x%prime[i]==0) 
        {
            cnt[prime[i]]--;
            x/=prime[i];
        }
        if(x==1) break;
        if(!a[x])
        {
            cnt[x]--;
            break;
        }
    }
}
ll power(int a,int y)
{
    ll b=a,res=1;
    while(y)
    {
        if(y&1) res=((res%p)*(b%p))%p;
        b=((b%p)*(b%p))%p;
        y=y>>1;
    }
    return res;
}
int main()
{
    freopen("flower.in","r",stdin);
    freopen("flower.out","w",stdout);
    n=read();m=read();p=read();
    mkp();
    for(int i=1;i<=tot;i++)
    if(m<n-m) m=n-m;
    for(int i=m+1;i<=n;i++) work1(i);
    for(int i=1;i<=n-m;i++) work2(i);
    for(int i=1;i<=tot;i++)
    {
        if(cnt[prime[i]])
        ans=((ans%p)*power(prime[i],cnt[prime[i]]))%p;
    }
    printf("%lld
",ans);
    return 0;
}