【问题描述】
由于去NOI的火车“堵”了数不清时间，小Z和小D打完ETG，闲着无聊开始看今年的JSOI省选题，并尝试着修改题目：
对于一个长度为L≥2的序列，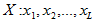
，如果满足对于任意的1≤i<j≤L，均有为质数，则他们把X称为一个“质数序列”。
现在有一个长度为N的序列，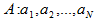
，他希望从中选取一个包含元素最多的子序列，使得这个子序列是一个质数序列。如果元素个数相同，则使子序列之和最大（在此意义下，保证有唯一解）。
因为他们还要xx，所以这个任务就交给你了。
【输入格式】
从文件 prime.in 中读入数据。
输入第一行包含一个正整数 N。
接下来一行包含N个正整数，依次描述。
【输出格式】
输出到文件 prime.out 中。
输出两行，第一行一个整数L，表示最长质数子序列的长度，第二行L个整数从小到大输出，表示最长质数子序列（元素个数相同，则使子序列之和最大）。
【样例输入】
3
2 3 4
【样例输出】
2
3 4
【数据规模与约定】
对于30%的数据满足。
对于60%的数据满足，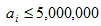
。
对于100%的数据满足，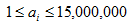
。
分析
首先来看一个性质
当两个数都大于1时
奇数+奇数=偶数（>2,不是质数）
偶数+偶数=偶数（不是质数）
所以当原序列中没有1时，原序列只可能有两个数且一个是奇数一个是偶数。
若序列中有1时，1+1=2，2是质数。设cnt为序列中1的个数
当cnt<2时，序列中最多可能有两个元素一奇一偶，所以直接可以用两重for循环分别枚举奇数和偶数，枚举出所有的排列判断它们的和是不是质数，最后保留最优解就行了。
当cnt>=2时，为了保证序列最长所有的1肯定是要保留的，此时序列中还可以再加进来一个偶数，我们再枚举所有偶数判断更新就行了。
50分
不考虑1的情况暴力枚举
100分
对有1的情况进行特判
代码
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=1000+5; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} return x*f; } int n,tot,cnt,ans,x1,x2; int a[maxn],ou[maxn],ji[maxn]; bool pd(int x) { if(x<2) return 0; for(int i=2;i*i<=x;i++) if(x%i==0) return 0; return 1; } int main() { freopen("prime.in","r",stdin); freopen("prime.out","w",stdout); n=read(); for(int i=1;i<=n;i++) { a[i]=read(); if(a[i]&1) ji[++ji[0]]=a[i]; else ou[++ou[0]]=a[i]; } sort(ji+1,ji+ji[0]+1); sort(ou+1,ou+ou[0]+1); while(ji[cnt+1]==1) cnt++; if(cnt<2) { for(int i=ji[0];i>=1;i--) for(int j=ou[0];j>=1;j--) { int tmp=ji[i]+ou[j]; if(pd(tmp)&&tmp>ans) { ans=tmp; x1=ji[i]; x2=ou[j]; } } if(x1>x2){int t=x1; x1=x2; x2=t;} printf("%d %d %d",2,x1,x2); }else if(cnt>=2) { for(int i=ou[0];i>=1;i--) if(pd(ou[i]+1)){ans=ou[i]; break;} if(ans!=0) printf("%d ",cnt+1); else printf("%d ",cnt); for(int i=1;i<=cnt;i++) printf("%d ",1); if(ans!=0) printf("%d",ans); } fclose(stdin); fclose(stdout); return 0; }