题目描述
小Z是一个小有名气的钢琴家,最近C博士送给了小Z一架超级钢琴,小Z希望能够用这架钢琴创作出世界上最美妙的音乐。
这架超级钢琴可以弹奏出n个音符,编号为1至n。第i个音符的美妙度为Ai,其中Ai可正可负。
一个“超级和弦”由若干个编号连续的音符组成,包含的音符个数不少于L且不多于R。我们定义超级和弦的美妙度为其包含的所有音符的美妙度之和。两个超级和弦被认为是相同的,当且仅当这两个超级和弦所包含的音符集合是相同的。
小Z决定创作一首由k个超级和弦组成的乐曲,为了使得乐曲更加动听,小Z要求该乐曲由k个不同的超级和弦组成。我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小Z想知道他能够创作出来的乐曲美妙度最大值是多少。
输入输出格式
输入格式:
输入第一行包含四个正整数n, k, L, R。其中n为音符的个数,k为乐曲所包含的超级和弦个数,L和R分别是超级和弦所包含音符个数的下限和上限。
接下来n行,每行包含一个整数Ai,表示按编号从小到大每个音符的美妙度。
输出格式:
输出只有一个整数,表示乐曲美妙度的最大值。
输入输出样例
4 3 2 3 3 2 -6 8
11
说明
共有5种不同的超级和弦:
1. 音符1 ~ 2,美妙度为3 + 2 = 5
2. 音符2 ~ 3,美妙度为2 + (-6) = -4
3. 音符3 ~ 4,美妙度为(-6) + 8 = 2
4. 音符1 ~ 3,美妙度为3 + 2 + (-6) = -1
5. 音符2 ~ 4,美妙度为2 + (-6) + 8 = 4最优方案为:乐曲由和弦1,和弦3,和弦5组成,美妙度为5 + 2 + 4 = 11。
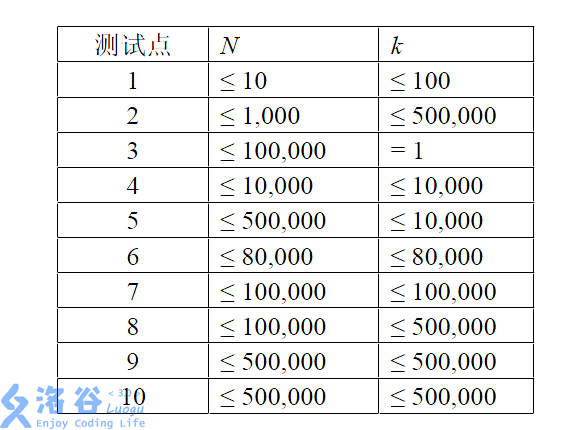
所有数据满足:-1000 ≤ Ai ≤ 1000,1 ≤ L ≤ R ≤ n且保证一定存在满足要求的乐曲。
分析
首先我们想一下k=1的情况,这就变成了求最大子段和。求最大子段和的做法是先记录前缀和,如果要求以i为开始的最大子段和,已知i的前缀和为s[i],现在就是要求一个最大的s[j],使s[j]-s[i]最大当然j要满足题目所给的条件,所以这个s[j]要尽可能的大,这个问题就转变为了区间求最大值。求区间最大值效率高的是RMQ算法。
如果k不等于1。那我们每次都要找一个最大的子段,我们就可以用二叉堆维护一个三元组(i,l,r),表示以i开头,另一端在l到r之间的最大值,每次取堆首就行了。
代码
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> using namespace std; typedef long long ll; const int maxn=500000+5; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} return x*f; } int n,k,l,r; int a[maxn],f[maxn][20],log2[maxn]; ll ans; struct node { int i,l,r,t; bool operator < (const node &j) const{ return a[t]-a[i-1]<a[j.t]-a[j.i-1]; } }; priority_queue<node>q; void prework() { log2[0]=-1; for(int i=1;i<=n;i++) log2[i]=log2[i>>1]+1; for(int j=1;j<=18;j++) for(int i=1;i+(1<<j)-1<=n;i++) { int t1=f[i][j-1],t2=f[i+(1<<(j-1))][j-1]; f[i][j]=a[t1]>a[t2]? t1:t2; } } inline int query(int l,int r) { if(l==r) return l; int t=log2[r-l+1]; int t1=f[l][t],t2=f[r-(1<<t)+1][t]; return a[t1]>a[t2]? t1:t2; } int main() { n=read();k=read();l=read();r=read(); for(int i=1;i<=n;i++) { a[i]=read(); a[i]=a[i-1]+a[i]; f[i][0]=i; } prework(); for(int i=1;i<=n;i++) if(i+l-1<=n) { int t=min(n,i+r-1); q.push((node){i,i+l-1,t,query(i+l-1,t)}); } for(int i=1;i<=k;i++) { node t=q.top(); q.pop(); ans+=a[t.t]-a[t.i-1]; if(t.t-1>=t.l)q.push((node){t.i,t.l,t.t-1,query(t.l,t.t-1)}); if(t.t+1<=t.r) q.push((node){t.i,t.t+1,t.r,query(t.t+1,t.r)}); } printf("%lld ",ans); return 0; }