计算机网络学习笔记 3.3 差错控制

一、产生差错的原因

概括来说，传输中的差错都是由于噪声引起的。

全局性

由于线路本身电气特性所产生的 随机噪声 （热噪声），是信道固有的，随机存在的。

解决办法：提高信噪比来减少或避免干扰。（对传感器下手）

局部性

外界特定的短暂原因所造成的 冲击噪声 ，是产生差错的 主要原因 。

解决办法：通常利用编码技术来解决。

二、差错类型

差错分为两类：

• 位错（比特错） 
  比特位出错，1变成0，0变成1
• 帧错 
  发送：[#1]-[#2]-[#3] 
  发生帧错：
  • 丢失：收到[#1]-[#3]
  • 重复：收到[#1]-[#2]-[#2]-[#3]
  • 失序：收到[#1]-[#3]-[(2]

链路层为网络层提供服务：无确认无连接服务，有确认无连接服务，有确认面向连接服务。

通信质量好、有线传输链路：不使用确认和重传机制

通信质量差的无线传输链路：使用确认和重传机制

三、差错控制

这里主要讨论比特错（位错）

冗余编码

在有效数据（信息位）发送之前，先按某种关系附加上一定的冗余位，构成一个符合某一规则的码字后再发送。

• 当要发送的有效数据变化时，相应的冗余位也随之变化，使码字遵从不变的规则。
• 接收端根据收到码字是否仍符合原规则，从而判断是否出错。

检错编码

检错编码都采用冗余编码技术。

• 仅能检查出错误，不能纠正错误
• 常见的检错编码有奇偶校验码和循环冗余码。

奇偶校验码

奇偶校验码是奇校验码和偶校验码的统称，它由n-1位信息元和1位校验元组成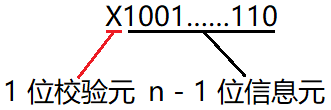 

奇校验码

• 在附加一个校验元后，码长为n的码字中"1"的个数为奇数

偶校验码

• 在附加一个校验元以后，码长为n的码字中"1"的个数为偶数

例： 
如果一个字符S的ASCI编码从低到高依次为1100101，采用奇校验，在下述收到的传输后字符中，哪种错误不能检测？

A. 11000011 B. 11001010 C. 11001100 D.11010011

答案：D

奇偶校验码特点

• 只能检查出 奇数个 比特错误，检错能力为 50% 。

例：11100100 奇校验：1 11100100

• 1位错：1 11100101，可以发现
• 2位错：1 01100101，不能发现

CRC循环冗余码

循环冗余码（Cyclic Redundancy Code，CRC）又称多项式码。

序列对应多项式

任何一个由二进制数位串组成的代码都可以与一个只含有0和1两个系数的多项式建立一一对应关系：

• 一个 k 位帧可以视为从 X ^k-1 到 X ⁰ 的 k 次多项式的系数序列，这个多项式的阶数为 k-1，高位是 X ^k-1 项的系数，下一位是 X ^k-2的系数，以此类推。

例： 
1110011有7位，表示成多项式是 X ⁵ +X ⁴ +X ² +X+1

多项式 X ⁶ +X ⁵ +X ⁴ +X+1 对应的数位串是 110110

模2除法

类似普通除法，按照模2运算规则，加法不进位，减法不借位，与 按位异或 相同。

计算： 按位异或

帧检验序列

给定一个 m bit的帧或报文，发送器生成一个 r bit的序列（位数有规定，即 r 是确定的），称为帧检验序列（FCS）。这样所形成的帧将由 m＋r 比特组成。

判断差错

发送方和接收方事先商定一个多项式G(x)（最高位和最低位必须为1），使这个带检验码的帧刚好能被预先确定的多项式 G(x) 整除。接收方用相同的多项式去除收到的帧，如果无余数，那么认为无差错。

计算冗余码

假设一个帧有m位，其对应的多项式为M(x)， 多项式 G(x) 的阶为 r，则计算冗余码的步骤如下：

1. 加0：在帧的低位端加上 r 个 0，得到被除数。
2. 模2除法。利用模2除法，用G(x)对应的数据串去除被除数，得到的余数即为冗余码（共 r 位，前面的 0 不可省略）。

例： 
要发送的数据是1101 0110 11，采用CRC校验，生成多项式是10011，那么最终发送的数据应该是?

答案： 
多项式阶数 r = 4，在要发送的数据后添加4个0得到被除数1101 0110 11 0000。用10011除被除数，得到余数1110，则帧检验序列（FCS）为1110。最终发送的数据是要发送的原数据拼接上帧检验序列，即1101 0110 11 1110。 
 
接收端检错 
把收到的每一个帧都除以同样的除数，然后检查得到的余数。

• 余数为0，判定这个帧没有差错，接受。
• 余数为不为0，判定这个帧有差错（无法确定到位）， 丢弃 。 
  FCS的生成以及接收端CRC检验都是 由硬件实现 ，处理很迅速，因此不会耽误数据的传输。

在数据链路层仅仅使用循环冗余检验CRC差错检测技术，只能做到对帧的无差错接收即“凡是接收端数据链路层接受的帧，我们都能以 非常接近于1的概率 认为这些帧在传输过程中没有产生差错”。接收端丢弃的帧虽然曾收到了，但是最终还是因为有差错被丢弃。

“凡是接收端数据链路层接收的帧均无差错”。

纠错编码

海明码

海明码：发现双比特错，只能纠正单比特错。

工作原理：动一发而牵全身

工作流程：

1. 确定校验码位数r
2. 确定校验码和数据的位置
3. 求出校验码的值
4. 检错并纠错

确定校验码位数r

海明不等式：2 ^r ≥ k + r + 1

r 为冗余信息位（校验位），k 为信息位，一共发送 k + r 位。

例：要发送的数据：D = 101101

数据的位数 k = 6，满足 2 ^r ≥ k + r + 1 的最小 r 为 4，也就是D = 101101 的海明码应该有 6 + 4 = 10位，男性英文名其中原数据 6 位，效验码 4 位。

确定校验码和数据的位置

假设这4位校验码分别为 P ₁ 、P ₂ 、P ₃ 、P ₄ ；数据从左到右为 D ₁ 、 D ₂ … D ₆

校验码放在 2 ⁿ 的位置，n = 0，1，…

例：要发送的数据：D = 101101，需插入校验码 P ₁ 、P ₂ 、P ₃ 、P ₄

海明码：

数据位	1	2	3	4	5	6	7	8	9	10
代码	P 1	P 2	D 1	P 3	D 2	D 3	D 4	P 4	D 5	D 6
值	待定	待定	1	待定	0	1	1	待定	0	1

求出校验码的值

1. 求二进制位数 
   看最后一个数据位数二进制表示是多少位 
   
   例：数据 D = 101101，数据位数为10，用二进制表示为1010，一共4位

2. 求二进制 
   将数据位用二进制表示

   二进制	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010
   代码	P 1	P 2	D 1	P 3	D 2	D 3	D 4	P 4	D 5	D 6
   值	待定	待定	1	待定	0	1	1	待定	0	1

3. 校验分组 
   P _i 校验二进制第 i 位 为 1 的数据 
   
   例：P ₁ 校验 D ₁ ，D ₂ ，D ₄ ，D ₅

   二进制	000 1	0010	001 1	0100	010 1	0110	011 1	1000	100 1	1010
   代码	P 1	P 2	D 1	P 3	D 2	D 3	D 4	P 4	D 5	D 6
   值	待定	待定	1	待定	0	1	1	待定	0	1

4. 确定校验位的值 
   校验位的值为被校验数据异或运算所得值 
   
   例：数据 D = 101101： 
   P ₁ = D ₁ ⊕ D ₂ ⊕ D ₄ ⊕ D ₅ = 1 ⊕ 0 ⊕ 1 ⊕ 0 = 0； 
   P ₂ = D ₁ ⊕ D ₃ ⊕ D ₄ ⊕ D ₆ = 1 ⊕ 1 ⊕ 1 ⊕ 1 = 0； 
   P ₃ = D ₂ ⊕ D ₃ ⊕ D ₄ = 0 ⊕ 1 ⊕ 1 = 0； 
   P ₄ = D ₅ ⊕ D ₆ = 0 ⊕ 1 = 1；

   二进制	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010
   代码	P 1	P 2	D 1	P 3	D 2	D 3	D 4	P 4	D 5	D 6
   值	0	0	1	0	0	1	1	1	0	1

   故101101的海明码为0010011101

检错并纠错

1. 计算错误位号 
   对于每个检错码 P _i ，与其校验的数据进行异或运算，得到错误位位号的第 i 位（从右往左数，二进制） S _i 
   
   例：101101 的海明码为 0010011101。假设第五位出错，因此接收到的数据位 0010 1 11101。 
   
   令所有要校验的位异或运算。

   二进制	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010
   代码	P 1	P 2	D 1	P 3	D 2	D 3	D 4	P 4	D 5	D 6
   值	0	0	1	0	1	1	1	1	0	1

   S ₁ = P ₁ ⊕ D ₁ ⊕ D ₂ ⊕ D ₄ ⊕ D ₅ = 0 ⊕ 1 ⊕ 1 ⊕ 1 ⊕ 0 = 1； 
   S ₂ = P ₂ ⊕ D ₁ ⊕ D ₃ ⊕ D ₄ ⊕ D ₆ = 0 ⊕ 1 ⊕ 1 ⊕ 1 ⊕ 1 = 0； 
   S ₃ = P ₃ ⊕ D ₂ ⊕ D ₃ ⊕ D ₄ = 0 ⊕ 1 ⊕ 1 ⊕ 1 = 1； 
   S ₄ = P ₄ ⊕ D ₅ ⊕ D ₆ = 1 ⊕ 0 ⊕ 1 = 0； 
   
   得到错误位为 S ₄ S ₃ S ₂ S ₁ = 0101

2. 纠错 
   若错误位号为 0，则说明无错，否则出错的位位号即为错误位号。 
   
   例：101101 的海明码为 0010011101，第五位出错。错误位为 0101 
   二进制序列为0101，恰好对应十进制 5，即出错位是第5位。

习题

1、为了纠正2比特的错误，编码的海明距应该为（ ）。

A. 2 B. 3 C. 4 D. 5

答案：B 
解析： 
海明码"纠错"d位，需要码距为 2d＋1 的编码方案；"检错"d位,，则只需码距为 d+1。