题目链接
题目大意
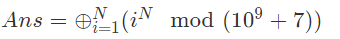
题目思路
前缀知识
积性函数指对于所有互质的整数a和b有性质\(f(ab)=f(a)f(b)\)的数论函数。
直接快速幂会nlogn会t
那么显然就要优化一下
令\(f(x)=x^n\)
显然\(f(a*b)=f(a)*f(b)\)
\(f(x)\)为完全积性函数则求出所有质因子的\(f(x)\),然后欧拉筛即可
代码
#include<bits/stdc++.h>
#define fi first
#define se second
#define debug cout<<"I AM HERE"<<endl;
using namespace std;
typedef long long ll;
const int maxn=1e7+3e6+5,inf=0x3f3f3f3f,mod=1e9+7;
const int eps=1e-6;
int n;
ll f[maxn],ans=1;
int prime[maxn],cnt;
bool isprime[maxn];
ll qpow(ll a,ll b){
ll ans=1,base=a;
while(b){
if(b&1){
ans=ans*base%mod;
}
base=base*base%mod;
b=b>>1;
}
return ans;
}
void getprime(int n){
for(ll i=2;i<=n;i++){//开ll因为后面要计算i*prime[j]
if(!isprime[i]){
prime[++cnt]=i;
f[i]=qpow(i,n);
}
for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
f[i*prime[j]]=f[i]*f[prime[j]]%mod;
isprime[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
ans^=f[i];
}
}
signed main(){
cin>>n;
getprime(n);
cout<<ans<<endl;
return 0;
}