马拉车算法

含义

就是一个\(O(n)\)的复杂度求解最长回文子串的算法

思路

思路的话我随便说下

首先回文串可能是奇数也可能是偶数，那么对称中心就有可能是两个字符的空隙，所以先给每个字符插如一个隔板符号 '|' 第0个字符插入'~' 防止出现超出边界的问题

如abcbs -> ~|a|b|c|b|s|

设\(p[i]\)以\(i\)为中点的回文半径包括自己本身

例如|a|b|a| 那么\(p[4]=4\)

我们也维护一个$ mx$ 和 \(id\)，表示对于当前计算的\([1,i-1]\)中，\(i + p[i]\) 的最大值是$ mx\(，\)mx \(对应的\) i \(记为\)id$

当你现在开始计算 p[i] 时，默认$ p[1..i-1] $都已经算出。如果 \(mx > i\)，那么根据对称得出

\(p[i] >= min(p[2 \times id - i], mx - i+1)\)

由下图可以看出

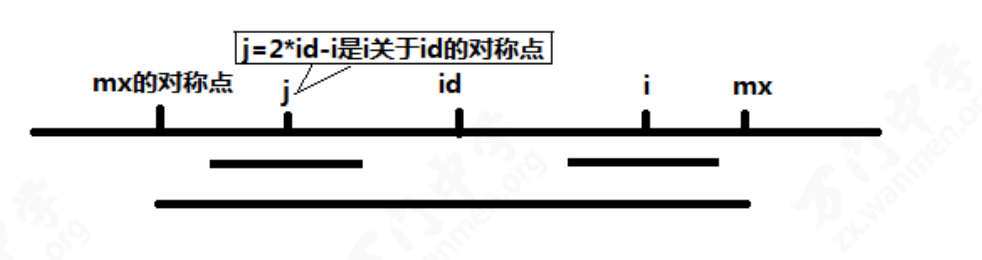
而最后的答案即为\(max(p[i])-1\)

很多人都没有解释为什么，其实很简单

根据\(p[i]\)的定义，那么扩展的回文串的长度即为\(2p[i]-1\)

而其中#占\(p[i]\)个，所以原回文串的长度即为\(p[i]-1\)

这个算法挺简单的，感觉比kmp都要简单很多

模板题

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//typedef pair<int,int> pii;
#define fi first
#define se second
#define debug printf("aaaaaaaaaaa\n");
const int maxn=2e7+5,inf=0x3f3f3f3f,mod=998244353;
const ll INF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-7;
char temp[maxn];
char s[maxn];
int p[maxn];
int main(){
    scanf("%s",temp+1);
    int n=strlen(temp+1);
    n=2*n+1;
    s[0]='~';
    for(int i=1;i<=n;i++){
        if(i%2){
            s[i]='|';
        }else{
            s[i]=temp[i/2];
        }
    }
    int mx=0,id=1,ans=0;
    for(int i=1;i<=n;i++){
        p[i]=min(p[2*id-i],mx-i+1);
        while(s[i+p[i]]==s[i-p[i]]) p[i]++;
        if(p[i]+i-1>=mx){
            mx=p[i]+i-1;
            id=i;
            ans=max(ans,p[i]-1);
        }
    }
    printf("%d\n",ans);
    return 0;
}