（整理自AndrewNG的课件，转载请注明。整理者：华科小涛@http://www.cnblogs.com/hust-ghtao/）
在遇到线性回归问题时，我们总是令。可是我们为什么这样选择代价函数呢？我们提到过是为了使目标变量（指
）的真实值和预测值的距离最小，想想也算合理。但是本篇博文将从概率的角度解释为什么这么选择代价函数，相信大家看完之后就会明白这个选择之后蕴含的更加深层次的原因。
首先，让我们假设：输入变量和目标变量满足等式，其中误差
表示在建模过程中没有考虑到的，但是对预测结果有影响的因素或者是指随机的噪声。根据实际观测和中心极限定理知，这些因素都服从正态分布，进一步假设这些误差之间是独立同分布的,则它们的和也服从正态分布，且均值为0，方差为
。上述结论可以写成：
，这表明
：
，其中符号表示以
为参数，给定
时
的分布。如果给定
（设计矩阵，包括所有的
）和
，则目标变量的分布可以写成：
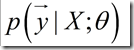，对于给定的，我们可以将它看成关于
的函数。从另一个角度，我们也可以把它看成是关于的函数，称为似然函数：
，由于已经假设之间独立同分布，这个公式可以写成：
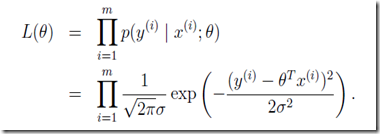，现在已经得出表示和
之间关系的概率模型，现在回到最初的问题，如何学习参数
？最大似然函数原理：我们应该选择使似然函数最大时对应的
值，因为这么选择，训练集中的对应的样本发生的概率是最大的。就是说，事件发生了，我们就认为此事件发生的概率是最大的。
所以我们要求出使取得最大值时的
：为方便计算，一般对似然函数取对数：
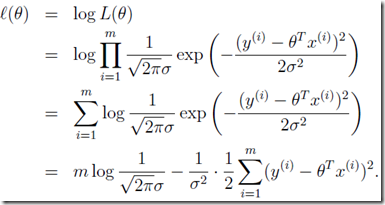，显然，使最大化，等价于是
最小化，这不就是我们最初选择的代价函数么？任务完成。
总结一下：通过对数据作出合理的概率假设，得出最小二乘回归可以使得似然函数取得最大值的结论。另外，在前面的回归方法中，我们没有考虑到方差的影响，此文章证明
的选择确实与
无关。在没有提出概率解释之前，我们用距离的概念解释了选择代价函数为最小二乘的合理性，本文又通过概率进行了解释，两方面互相呼应，使理解更加深刻。一点点小体会：要多读书，只有博采众长，才可以相互印证。