继续总结一下RCNN系列。上篇RCNN- 将CNN引入目标检测的开山之作 介绍了CNN用于目标检测的基本思想和流程。后续出现了SPPnet,Fast-RCNN ,Faster-RCNN等一些列改进。最终实现了端对端学习,同时带来速度与精度的提升。
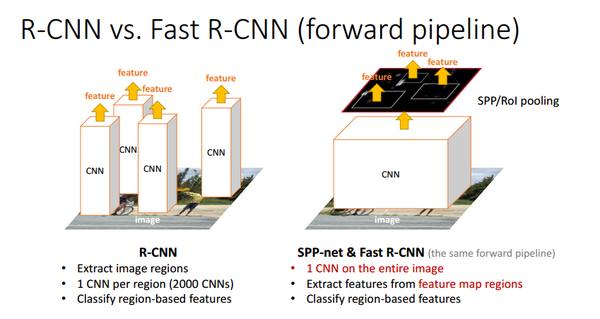
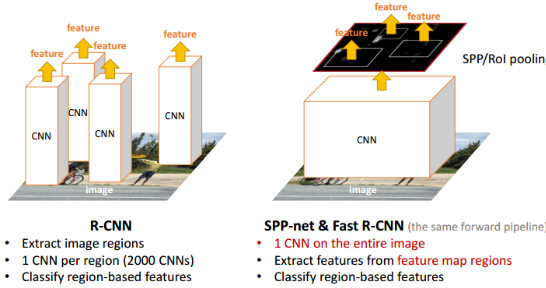
在RCNN中CNN阶段的流程大致如下:
红色框是selective search 输出的可能包含物体的候选框(ROI)。
一张图图片会有~2k个候选框,每一个都要单独输入CNN做卷积等操作很费时。SPP-net提出:能否在feature map上提取ROI特征,这样就只需要在整幅图像上做一次卷积。
虽然总体流程还是 Selective Search得到候选区域->CNN提取ROI特征->类别判断->位置精修,但是由于所有ROI的特征直接在feature map上提取,大大减少了卷积操作,提高了效率。
有两个难点要解决:
1. 原始图像的ROI如何映射到特征图(一系列卷积层的最后输出)
2. ROI的在特征图上的对应的特征区域的维度不满足全连接层的输入要求怎么办(又不可能像在原始ROI图像上那样进行截取和缩放)?
【空间金字塔池化 (Spatial Pyramid Pooling)】
对于难点2我们分析一下:
-
这个问题涉及的流程主要有: 图像输入->卷积层1->池化1->...->卷积层n->池化n->全连接层。
- 引发问题的原因主要有:全连接层的输入维度是固定死的,导致池化n的输出必须与之匹配,继而导致图像输入的尺寸必须固定。
不就是为了使一些列卷积层的最后输出刚维度好是全连接层的输入维度吗?聪明的你有没有好的解决办法?先思考几秒钟。
解决办法可能有:
- 想办法让不同尺寸的图像也可以使 池化n 产生固定的 输出维度。(打破图像输入的固定性)
- 想办法让全连接层(罪魁祸首)可以接受非固定的输入维度。(打破全连接层的固定性,继而 也打破了图像输入的固定性)
- 其它方法(肯定不止这两个解决办法,读者有新想法欢迎交流)
以上的方法1就是SPPnet的思想。它在池化n 的地方做了一些手脚 (特殊池化手段:空间金字塔池化),使得 不同尺寸的图像也可以使 池化n 产生固定的 输出维度。
(至于方法2 其实就是全连接转换为全卷积,作用的效果等效为在原始图像做滑窗,多个窗口并行处理,具体方法日后在写)
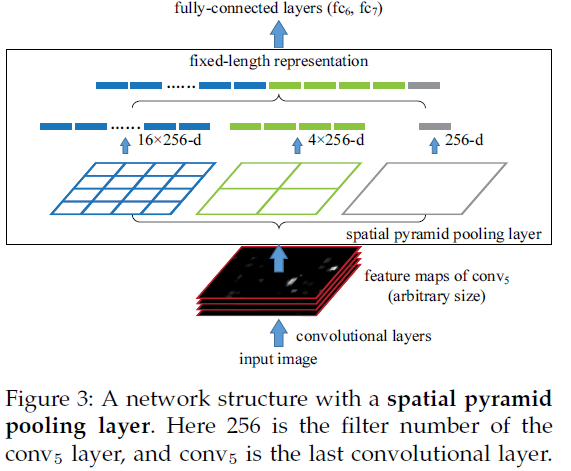
所谓空间金字塔池化就是沿着 金字塔的低端向顶端 一层一层做池化。
假设原图输入是224x224,对于conv5出来后的输出是13x13x256的,可以理解成有256个这样的filter,每个filter对应一张13x13的reponse
map。如果像上图那样将reponse map分成1x1(金字塔底座),2x2(金字塔中间),4x4(金字塔顶座)三张子图,分别做max pooling后,出来的特征就是(16+4+1)x256 维度。如果原图的输入不是224x224,出来的特征依然是(16+4+1)x256维度。这样就实现了不管图像尺寸如何 池化n 的输出永远是 (16+4+1)x256 维度。
实际运用中只需要根据全连接层的输入维度要求设计好空间金字塔即可。
【整幅图像做一次卷积】
将conv5的pool层改为SPP之后就不必把每一个都ROI抠出来送给CNN做繁琐的卷积了,整张图像做卷积一次提取所有特征再交给SPP即可。
R-CNN重复使用深层卷积网络在~2k个窗口上提取特征,特征提取非常耗时。SPPNet将比较耗时的卷积计算对整幅图像只进行一次,之后使用SPP将窗口特征图池化为一个固定长度的特征表示。如下图 第二个流程:
(备注:还有难点1没有提,找了一些资料看,总感觉没有彻底搞清楚,有些公式不知怎么推导得到的,改日再写吧)
参考:
-
RCNN学习笔记(3):Spatial Pyramid
Pooling in Deep Convolutional Networks for Visual Recognition(SPP-net)
-
http://mp7.watson.ibm.com/ICCV2015/slides/iccv2015_tutorial_convolutional_feature_maps_kaiminghe.pdf
- 《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition 》

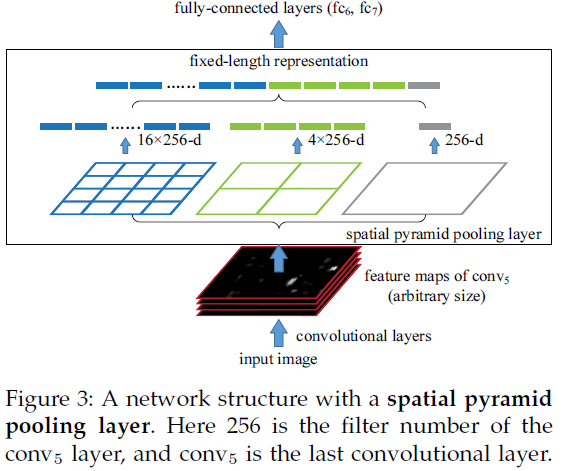 假设原图输入是224x224,对于conv5出来后的输出是13x13x256的,可以理解成有256个这样的filter,每个filter对应一张13x13的reponse
map。如果像上图那样将reponse map分成1x1(金字塔底座),2x2(金字塔中间),4x4(金字塔顶座)三张子图,分别做max pooling后,出来的特征就是(16+4+1)x256 维度。如果原图的输入不是224x224,出来的特征依然是(16+4+1)x256维度。这样就实现了不管图像尺寸如何 池化n 的输出永远是 (16+4+1)x256 维度。
假设原图输入是224x224,对于conv5出来后的输出是13x13x256的,可以理解成有256个这样的filter,每个filter对应一张13x13的reponse
map。如果像上图那样将reponse map分成1x1(金字塔底座),2x2(金字塔中间),4x4(金字塔顶座)三张子图,分别做max pooling后,出来的特征就是(16+4+1)x256 维度。如果原图的输入不是224x224,出来的特征依然是(16+4+1)x256维度。这样就实现了不管图像尺寸如何 池化n 的输出永远是 (16+4+1)x256 维度。