排序算法五：交换排序之快速排序

排序算法五：交换排序之快速排序

---

声明：引用请注明出处http://blog.csdn.net/lg1259156776/

---

引言

在我的博文《“主宰世界”的10种算法短评》中给出的首个算法就是高效的排序算法。本文将对排序算法做一个全面的梳理，从最简单的“冒泡”到高效的堆排序等。

系列博文的前三篇讲述了插入排序的三种不同类型，本文讲述第二大类的排序算法：交换排序，包括冒泡排序和快速排序。

---

排序相关的的基本概念

• 排序：将一组杂乱无章的数据按一定的规律顺次排列起来。
  
  • 数据表( data list): 它是待排序数据对象的有限集合。
  • 排序码(key):通常数据对象有多个属性域，即多个数据成员组成,其中有一个属性域可用来区分对象,作为排序依据。该域即为排序码。每个数据表用哪个属性域作为排序码，要视具体的应用需要而定。
• 分类
  
  • 内排序：指在排序期间数据对象全部存放在内存的排序；
  • 外排序：指在排序期间全部对象个数太多，不能同时存放在内存，必须根据排序过程的要求，不断在内、外存之间移动的排序。

---

排序算法的分析

排序算法的稳定性

如果在对象序列中有两个对象r[i]和r[j] ,它们的排序码k[i]==k[j] 。如果排序前后,对象r[i]和r[j] 的相对位置不变，则称排序算法是稳定的；否则排序算法是不稳定的。

排序算法的评价

时间开销

• 排序的时间开销可用算法执行中的数据比较次数与数据移动次数来衡量。
• 算法运行时间代价的大略估算一般都按平均情况进行估算。对于那些受对象排序码序列初始排列及对象个数影响较大的，需要按最好情况和最坏情况进行估算

空间开销

算法执行时所需的附加存储。

---

交换排序

交换排序的基本思想是：两两比较待排序记录（数据表）的关键字（排序码），发现两个记录的次序相反时即进行交换，直到没有反序的记录为止。主要包括冒泡排序和快速排序。

---

快速排序

基本思想

• 任选一个记录，以其关键字为“枢轴”，序列中比它小的移动到该记录之前，反之移动到它之后。
• 通过一趟排序将待排的记录分割成两个区域，一个区域中记录的关键字比另一个区域的关键字小（一次划分）。
• 然后左右两边分别处理进行相同的操作直到排好。

快速排序是一个递归算法，平均时间复杂度为O(nlog(n))，inplace操作，需要最小的额外内存。

图示

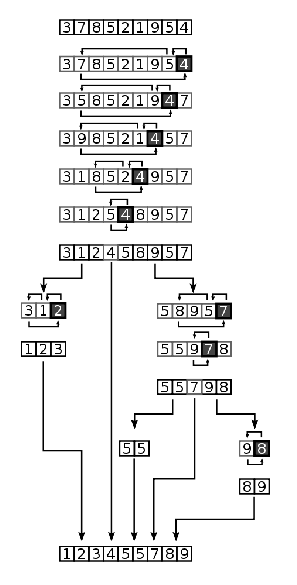
图中很清楚的描述了数据表以4分割为两个子数据表，然后两个自数据表再分别以2和7继续分割为4个数据表，就这样一直递归到不能再分割为止，然后构成的整个已经完成排序的数据表。

####快速排序的c plus plus描述

#include <iostream>
#include <iomanip>

using namespace std;

#define SIZE 9

/* swap a[i] and a[j] */
void swap(int a[], int i, int j)
{   
    int temp;
    temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}

void print(const int arr[])
{
    for(int i=0;i < SIZE; i++) {
        cout << setw(3) << arr[i];
    }
    cout << endl;
}

/* sort arr[left]...arr[right] into increasing order */
void qsort(int a[], int left_index, int right_index)
{
    int left, right, pivot;
    if(left_index >= right_index) return;

    left = left_index;
    right = right_index;

        // pivot selection
    pivot = a[(left_index + right_index) /2];

        // partition
    while(left <= right) {
        while(a[left] < pivot) left++;
        while(a[right] > pivot) right--;
        if(left <= right) {
            swap(a,left,right);
            left++; right--;
        }
        print(a);       
    }

        // recursion
    qsort(a,left_index,right);
    qsort(a,left,right_index);
}

int main()
{
    int a[SIZE]={1, 12, 5, 26, 7, 14, 3, 7, 2};
    print(a);
    qsort(a,0,SIZE-1);
}

输出为：

  1 12  5 26  7 14  3  7  2
  1  2  5 26  7 14  3  7 12
  1  2  5  7  7 14  3 26 12
  1  2  5  7  3 14  7 26 12
  1  2  5  7  3 14  7 26 12
  1  2  3  7  5 14  7 26 12
  1  2  3  7  5 14  7 26 12
  1  2  3  7  5 14  7 26 12
  1  2  3  5  7 14  7 26 12
  1  2  3  5  7  7 14 26 12
  1  2  3  5  7  7 14 12 26
  1  2  3  5  7  7 12 14 26

运行中的细节为：

1 12  5 26  7 14  3  7  2
1 12 5 26 7 14 3 7 2
  pivot element = 7
  swap(12,2)
  1  2  5 26  7 14  3  7 12
  swap(26,7)
  1  2  5  7  7 14  3 26 12
  swap(7,3)
  1  2  5  7  3 14  7 26 12
  1  2  5  7  3 14  7 26 12
1 2 5 7 3
  pivot element = 5
  swap(5,3)
  1  2  3  7  5 14  7 26 12
  1  2  3  7  5 14  7 26 12
1 2 3
  pivot element = 2
  swap(2,2)
  1  2  3  7  5 14  7 26 12
7 5
  pivot element = 7
  swap(7,5)
  1  2  3  5  7 14  7 26 12
14 7 26 12
  pivot element = 7
  swap(14,7)
  1  2  3  5  7  7 14 26 12
14 26 12
  pivot element = 26
  swap(26,12)
  1  2  3  5  7  7 14 12 26
14 12
  pivot element = 14
  swap(14,12)
  1  2  3  5  7  7 12 14 26

上面给出的算法实现中使用的是直接取区间中间位置的值作为轴来调整，最后得到的right值作为下一个左区间的右值，而left作为下一个右区间的左值，从而实现递归完成。从这个运行的细节可以看出整个快速排序算法的执行过程。

算法分析

最好情况：每次划分所取的基准都是当前无序区的”中值”记录，划分的结果是基准的左、右两个无序子区间的长度大致相等。总的关键字比较次数：0(nlgn)。
最坏情况：每次划分选取的基准都是当前无序区中关键字最小(或最大)的记录，划分的结果是基准左边的子区间为空(或右边的子区间为空)，而划分所得的另一个非空的子区间中记录数目，仅仅比划分前的无序区中记录个数减少一个。因此，快速排序必须做n-1次划分，第i次划分开始时区间长度为n-i+1，所需的比较次数为n-i(1≤i≤n-1)，故总的比较次数达到最大值：n(n−1)/2=O(n2)。

因为快速排序的记录移动次数不大于比较的次数，所以快速排序的最坏时间复杂度应为0(n2)，最好时间复杂度为O(nlgn)。但就平均性能而言，它是基于关键字比较的内部排序算法中速度最快者，快速排序亦因此而得名。它的平均时间复杂度为O(nlgn)。

快速排序是非稳定的。

快速排序在系统内部需要一个栈来实现递归。若每次划分较为均匀，则其递归树的高度为O(lgn)，故递归后需栈空间为O(lgn)。最坏情况下，递归树的高度为O(n)，所需的栈空间为O(n)。

基准关键字的选择

在当前无序区中选取划分的基准关键字是决定算法性能的关键。

1. “三者取中”的规则。
   “三者取中”规则，即在当前区间里，将该区间首、尾和中间位置上的关键字比较，取三者之中值所对应的记录作为基准。

2. 取位于low和high之间的随机数k(low≤k≤high)，用R[k]作为基准。
   选取基准最好的方法是用一个随机函数产生一个取位于low和high之间的随机数k(low≤k≤high)，用R[k]作为基准，这相当于强迫R[low..high]中的记录是随机分布的。用此方法所得到的快速排序一般称为随机的快速排序。

---

附录

以下为使用最右边元素作为分割轴并采用模板类实现的快速排序算法。

#include <iostream>
using namespace std;

template<class T>
void exchg(T &a, T &b)
{
    T tmp = b;
    b = a;
    a = tmp;
}

template<class T>
int partition(T a[], int left, int right)
{
    T pivot = a[right];
    int i = left - 1;
    int j = right;
    for(;;)
    {
        while(a[--j] > pivot);
        while(a[++i] < pivot);
        if(i >= j) break;
        exchg(a[i], a[j]);
    }
    exchg(a[right], a[i]);
    return i;
}

template<class T>
void quick(T a[], int left, int right)
{
    if(left >= right) return;
    int p = partition(a, left, right);
    quick(a, left, p-1);
    quick(a, p+1, right);
}

int main()
{
    char a[] = {'A','S','O','R','T','I','N','G',
                'E','X','A','M','P','L','E'};
    quick(a, 0, sizeof(a)/sizeof(a[0])-1);
    return 0;
}

---

2015-9-25 艺少