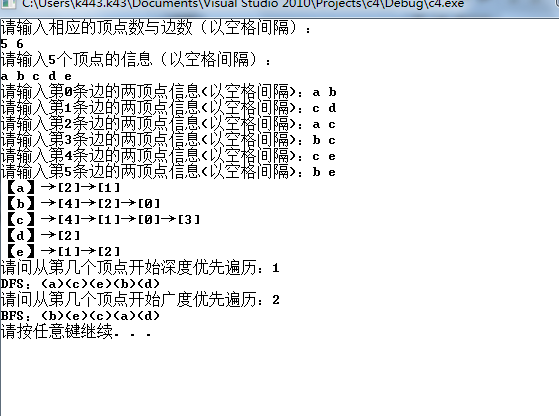
/* 首先,根据用户输入的顶点总数和边数,构造无向图,然后以用户输入的顶点 为起始点,进行深度优先、广度优先搜索遍历,并输出遍历的结果。 */ #include <stdlib.h> #include <iostream> #define MVNum 100 //最大的顶点数 using namespace std; /*——————图的邻接表存储表示——————*/ //边的结点表-在顶点表后面 typedef struct ArcNode { int adjvex; //邻接点域-该边所指向顶点的位置下标 struct ArcNode* nextarc; //链域-邻接的下一顶点位置 //otherInfo info; //用来纪录权值 }ArcNode; //单链表表头-结构体(类似于头结点) typedef struct VNode { char data; //顶点的信息值 ArcNode* firstarc; //指向第一条依附该顶点的下一结点-指向类型为边ArcNode }VNode, AdjList[MVNum]; //AdjList邻接表类型 //图ALGraph typedef struct { AdjList vertices; //定义一个邻接表类型,vertices最多有MVNum个 int vexnum; //顶点数 int arcnum; //边数 }ALGraph; //链队列结构体 typedef struct QNode { int data; struct QNode* next; }QNode,*QueuePtr; //链队头指针结构体 typedef struct { QueuePtr front; //队头 QueuePtr rear; //队尾 }LinkQueue; //寻找v1,v2的下标 int LocateVex(ALGraph& G, char NodeInfo) { int flag = 0; //匹配NodeInfo for (int i = 0; i < G.vexnum; i++) { if (G.vertices[i].data == NodeInfo) { flag = i; return i; break; } } if (flag) return flag; else exit(errno); } //邻接表生成无边图 void CreateUDG(ALGraph& G) { //输入数据 cout << "请输入相应的顶点数与边数(以空格间隔):" << endl; cin >> G.vexnum >> G.arcnum; //初始化顶点信息 cout << "请输入" << G.vexnum << "个顶点的信息(以空格间隔):" << endl; for (int i = 0; i < G.vexnum; i++) { cin >> G.vertices[i].data; G.vertices[i].firstarc = NULL; //各顶点结点的指针域置空 } //初始化边的连接信息 for (int i = 0; i < G.arcnum; i++) { char v1, v2; //v1,v2为一条边连接的两个顶点 cout << "请输入第" << i << "条边的两顶点信息(以空格间隔):"; cin >> v1 >> v2; //求v1,v2在vertices的下标 int idx_v1 = LocateVex(G, v1); int idx_v2 = LocateVex(G, v2); //调用边的结点表,生成以v1为头结点的单链表构成的邻接表 ArcNode* p1 = new ArcNode; //生成第一个边连接的结点(后面的那一个) p1->adjvex = idx_v2; //存入结点的下标 //关联头结点,用头插法,插入结点 p1->nextarc = G.vertices[idx_v1].firstarc; G.vertices[idx_v1].firstarc = p1; //调用边的结点表,生成以v2为头结点的单链表构成的邻接表 ArcNode* p2 = new ArcNode; //生成第一个边连接的结点(后面的那一个) p2->adjvex = idx_v1; //存入结点的下标 //关联头结点,用头插法,插入结点 p2->nextarc = G.vertices[idx_v2].firstarc; G.vertices[idx_v2].firstarc = p2; } } //邻接表的遍历 void TraverseAdjList(ALGraph& G) { for (int i = 0; i < G.vexnum; i++) { cout << "【" << G.vertices[i].data << "】→"; //临时头指针用于遍历 ArcNode* temp = G.vertices[i].firstarc; //当temp不为空,输出链表 while (temp) { //输出顶点序号 cout<<"["<<temp->adjvex<<"]"; temp=temp->nextarc; if (temp) cout << "→"; } putchar(10); } } //深度优先遍历 int visisted_D[MVNum] = { 0 }; //辅助数组 void DFS_AL(ALGraph& G, int v) { //从v顶点开始访问 cout <<"("<< G.vertices[v].data <<")"; //访问过后置1 visisted_D[v] = 1; //临时结点用于遍历,指向头结点后一结点 ArcNode *temp = G.vertices[v].firstarc; //循环遍历 while (temp) { int w = temp->adjvex; //如果辅助数组visisted[w] == 0递归调用DFS_AL if (visisted_D[w] == 0) { DFS_AL(G, w); } //temp指向下一结点 temp = temp->nextarc; } } //广度优先遍历 int visisted_B[MVNum] = { 0 }; //辅助数组 //队列初始化 void InitQuenue(LinkQueue& Q) { Q.rear = new QNode; Q.front = Q.rear; Q.front->next = NULL; } //入队-尾插法 void EnQuenue(LinkQueue& Q,int v) { QNode* cur = new QNode; cur->data = v; cur->next = NULL; Q.rear->next = cur; Q.rear = cur; } //出队-返回队头int u void DeQuenue(LinkQueue& Q, int &u) { QNode* temp = Q.front->next; Q.front->next = temp->next; //队头u更新 u = temp->data; //如果最后一个被删,队尾指向队头 if (Q.rear == temp) { Q.rear = Q.front; } delete temp; } //返回u的第一个邻结点 int FirstAdjvex(ALGraph& G, int u) { int w = G.vertices[u].firstarc->adjvex; return w; } //返回u的下一个邻结点 int NextAdjVex(ALGraph& G, int u, int w) { //临时结点temp指向头结点的第一个邻结点,w此时为第一结点序号 ArcNode *temp = G.vertices[u].firstarc; while (temp->adjvex != w) { temp = temp->nextarc; } //若w结点的下一结点不为空,返回结点序号w的下一结点序号 if (temp->nextarc) return temp->nextarc->adjvex; //否则返回-1,使其退出循环 else return -1; delete temp; } void BFS_AL(ALGraph& G, int v) { //从v顶点开始访问 cout << "(" << G.vertices[v].data << ")"; //访问过后置1 visisted_B[v] = 1; //创建队列 LinkQueue Q; InitQuenue(Q); EnQuenue(Q,v); int u = v; //用于找邻接点 //队列非空出队 while (Q.rear != Q.front) { //出队,并把队头置为u DeQuenue(Q, u); for (int w = FirstAdjvex(G, u); w >= 0; w = NextAdjVex(G, u, w)) { //若结点序号w未访问则进行访问 if (!visisted_B[w]) { cout << "(" << G.vertices[w].data << ")"; //输出数据 visisted_B[w] = 1; //打上访问标记 EnQuenue(Q, w); //将结点w入队 } }//进行下一次w的邻结点查找 } } void main() { ALGraph G; //邻接表生成无边图 CreateUDG(G); //遍历邻接表 TraverseAdjList(G); //深度优先遍历 cout << "请问从第几个顶点开始深度优先遍历:"; int v; cin >> v; cout << "DFS:"; DFS_AL(G, v-1); putchar(10); //广度优先遍历 cout << "请问从第几个顶点开始广度优先遍历:"; cin >> v; cout << "BFS:"; BFS_AL(G, v - 1); putchar(10); system("pause"); }
//深度优先遍历由递归实现。也可用栈来实现(与BFS队列操作类似)。
//广度优先遍历由队列实现。需要先让开始进行遍历的顶点入队,再进行出队,但是出队需保存出队的结点序号值作为表头,用于遍历该层,并同时将辅助数组visisted_B[v]置为1,以表示已经访问,然后根据邻接表结构进行类似于树的层次遍历操作,每个结点访问过后都要将visisted_B[v]置为1,当其中一层遍历完过后,先进的第一个结点出队,并更新出队值,同时开始遍历以该结点序号为头结点的单链表,直到每层遍历完后结束。
//在广度优先遍历过程中,进行出队操作时,一开始用形参int u来进行接收,导致队头值u(表头)无法更新,造成只能遍历初始顶点的那一条单链表,后改为形参 int &u解决队头值更新问题。