坑死了......
题意:给你个有向图,你需要把点分成k种,满足每条边都是分层的(从i种点连向i + 1种点,从k连向1)。
要确保每种点至少有一个。
求k的最大值,最小值。
n <= 1e5, m <= 1e6, k >= 3。
解:
首先可以发现,如果存在一个环,那么k一定是环长的约数。
然后我们把所有环长的gcd求出来就行了......
考虑这几种情况:
情况①:

这启示我们要拓扑排序或建反向边。鉴于这个图可能有环,我们建长度为-1的反向边。
情况②:
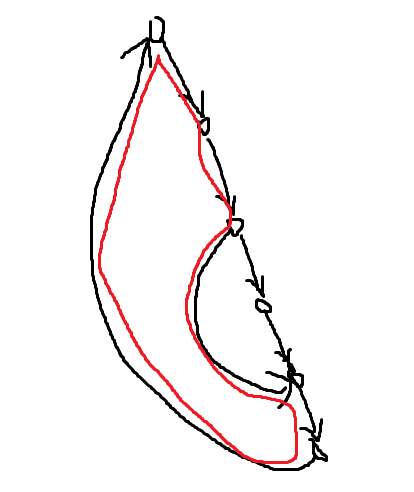
这个红色的环怎么办?
事实上只要别的两个环满足了,这个组合起来的环也能够被满足(意会一下)。
情况⑨:
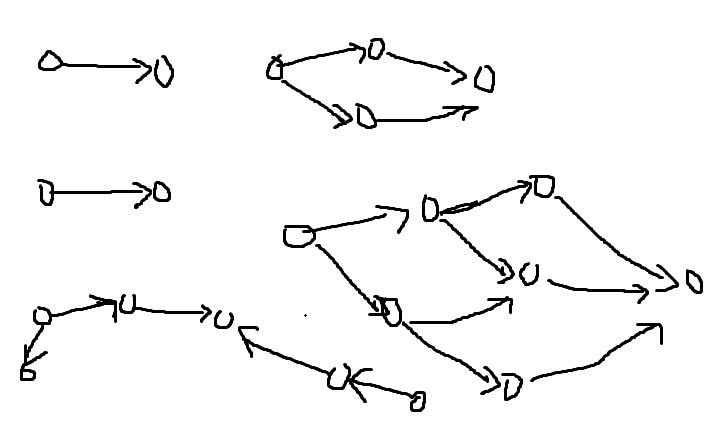
这启示我们在无环/环长全部为0的时候进行特殊处理。
然后写代码的时候出了一堆错......50分暴力发现比正解还难打,不会写......

1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 5 const int N = 100010, M = 1000010, INF = 0x3f3f3f3f; 6 7 struct Edge { 8 int nex, v, len; 9 }edge[M << 1]; int top = 1; 10 11 int e[N], m, n, vis[N], small, large, fd, g; 12 13 int gcd(int a, int b) { 14 if(!b) { 15 return a; 16 } 17 return gcd(b, a % b); 18 } 19 20 inline void add(int x, int y, int z) { 21 top++; 22 edge[top].nex = e[x]; 23 edge[top].len = z; 24 edge[top].v = y; 25 e[x] = top; 26 return; 27 } 28 29 void DFS(int x, int in_e) { // error : in_edge space 30 small = std::min(small, vis[x]); 31 large = std::max(large, vis[x]); 32 //printf("vis[%d] = %d ", x, vis[x]); 33 for(int i = e[x]; i; i = edge[i].nex) { 34 if((i ^ 1) == in_e) { 35 continue; 36 } 37 int y = edge[i].v; 38 if(vis[y] == INF) { 39 vis[y] = edge[i].len + vis[x]; 40 DFS(y, i); 41 } 42 else { 43 int cir = abs(edge[i].len + vis[x] - vis[y]); // error : abs(vis[x] - vis[y]) + 1 44 //printf(">_< >>> [%d]%d [%d]%d ", x, vis[x], y, vis[y]); 45 //printf("cir = %d ", cir); 46 g = gcd(g, cir); 47 fd = 1; 48 } 49 } 50 return; 51 } 52 53 int main() { 54 55 scanf("%d%d", &n, &m); 56 for(int i = 1, x, y; i <= m; i++) { 57 scanf("%d%d", &x, &y); 58 add(x, y, 1); 59 add(y, x, -1); 60 } 61 memset(vis, 0x3f, sizeof(vis)); 62 int lenth = 0; 63 for(int i = 1; i <= n; i++) { 64 if(vis[i] == INF) { 65 large = small = 1; 66 vis[i] = 1; 67 DFS(i, 0); 68 lenth += large - small + 1; 69 } 70 } 71 72 //printf("fd = %d ", fd); 73 74 if(!fd || !g) { // error : !g space 75 if(n <= 2 || lenth <= 2) { // error : lenth <= 2 space 76 printf("-1 -1"); 77 } 78 else { 79 printf("%d 3", lenth); 80 } 81 return 0; 82 } 83 if(g < 3) { 84 printf("-1 -1"); 85 } 86 else { 87 printf("%d ", g); 88 for(int i = 3; i <= g; i++) { 89 if(g % i == 0) { 90 printf("%d", i); 91 break; 92 } 93 } 94 } 95 96 return 0; 97 }
太毒瘤了......
