
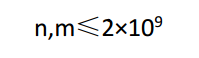
解:先推一个式子,然后就是CRT了...
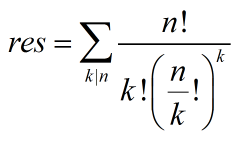
那个阶乘怎么求呢?主要是分母可能有0,这时我们把分母的因子p全部提出来,上下次数相减判断即可。
细节颇多......注意在快速幂开始的时候a %= MO是个好习惯。

1 #include <cstdio> 2 #include <algorithm> 3 4 typedef long long LL; 5 const int N = 100010; 6 const LL MO = 1e9 - 401, mod[] = {0, 2, 13, 5281, 7283}; 7 8 int turn; 9 LL ans[5], n, m, nn[10000][5]; 10 //LL inv[10000][5], invn[10000][5]; 11 12 inline LL qpow(LL a, LL b, LL c) { 13 LL ans = 1; 14 a %= c; 15 while(b) { 16 if(b & 1) ans = ans * a % c; 17 a = a * a % c; 18 b = b >> 1; 19 } 20 return ans; 21 } 22 23 inline LL Pow(LL a, LL b) { 24 LL ans = 1; 25 while(b) { 26 if(b & 1) ans = ans * a; 27 a = a * a; 28 b = b >> 1; 29 } 30 return ans; 31 } 32 33 LL exgcd(LL a, LL &x, LL b, LL &y) { 34 if(!b) { 35 x = 1; y = 0; 36 return a; 37 } 38 LL g = exgcd(b, x, a % b, y); 39 std::swap(x, y); 40 y -= x * (a / b); 41 return g; 42 } 43 44 inline LL getnn(LL x) { 45 if(!x) return 1; 46 LL t = x / mod[turn]; 47 LL ans = qpow(nn[mod[turn] - 1][turn], t, mod[turn]); 48 t = x % mod[turn]; 49 return ans * nn[t][turn] % mod[turn] * getnn(x / mod[turn]); 50 } 51 52 inline LL cal(LL k) { 53 54 //printf("cal %lld ", k); 55 //bool f = (turn == 2 && k == 2) || (turn == 2 && k == 1); 56 57 LL time = 0; 58 for(LL i = n; i > 1; i /= mod[turn]) { 59 time += i / mod[turn]; 60 //printf("1 time += %lld = %lld ", i / mod[turn], time); 61 } 62 for(LL i = k; i > 1; i /= mod[turn]) { 63 time -= i / mod[turn]; 64 //printf("2 time -= %lld = %lld ", i / mod[turn], time); 65 } 66 for(LL i = n / k; i > 1; i /= mod[turn]) { 67 time -= (i / mod[turn]) * k; 68 //printf("3 time -= %lld = %lld ", i / mod[turn], time); 69 } 70 if(time) { 71 //printf(" -- -- return 0 "); 72 //printf("mod = %lld ans = 0 ", mod[turn]); 73 return 0; 74 } 75 76 LL t1 = getnn(n), t2 = getnn(k), t3 = getnn(n / k); 77 /*if(f) { 78 printf("%lld %lld %lld ", t1, t2, t3); 79 }*/ 80 t3 = qpow(t3, k, mod[turn]); 81 t2 = qpow(t2, mod[turn] - 2, mod[turn]); 82 t3 = qpow(t3, mod[turn] - 2, mod[turn]); 83 84 //printf("return %lld ", t1 * t2 % mod[turn] * t3 % mod[turn]); 85 //printf("mod = %lld k = %lld ans = %lld ", mod[turn], k, t1 * t2 % mod[turn] * t3 % mod[turn]); 86 return t1 * t2 % mod[turn] * t3 % mod[turn]; 87 } 88 89 inline LL solve() { /// cal each prime 90 LL ans = 0; 91 for(LL i = 1; i * i <= n; i++) { 92 if(n % i) continue; 93 ans = (ans + cal(i)) % mod[turn]; 94 if(i * i < n) { 95 ans = (ans + cal(n / i)) % mod[turn]; 96 } 97 } 98 return ans; 99 } 100 101 inline void work() { 102 scanf("%lld%lld", &n, &m); 103 //m %= MO; 104 105 for(turn = 1; turn <= 4; turn++) { 106 ans[turn] = solve(); 107 //printf("ans %d %lld = %lld ", turn, mod[turn], ans[turn]); 108 } 109 110 111 /// excrt 112 /*LL a = ans[1], p = mod[1]; 113 for(int i = 2; i <= 4; i++) { 114 /// merge 115 //printf("merge %d ", i); 116 LL P = p * mod[i], x, y; 117 LL c1 = ((a - ans[i]) % P + P) % P; 118 //printf("a = %lld c1 = %lld ", a, c1); 119 LL g = exgcd(mod[i], x, p, y); 120 (x *= (c1 / g)) %= P; (y *= (c1 / g)) %= P; 121 a = (x * mod[i] % P + ans[i]) % P; 122 p = P; 123 //printf("merge %lld ans = %lld ", mod[i], a); 124 }*/ 125 /// crt 126 LL a = 0, p = MO - 1; 127 for(int i = 1; i <= 4; i++) { 128 a = (a + ans[i] * (p / mod[i]) % p * qpow(p / mod[i], mod[i] - 2, mod[i]) % p) % p; 129 } 130 131 //printf("over "); 132 a = (a % p + p) % p; 133 //printf("a = %lld ", a); 134 LL ans = qpow(m, a, MO); 135 printf("%lld ", ans); 136 return; 137 } 138 139 inline void prework() { 140 for(turn = 1; turn <= 4; turn++) { 141 //invn[0][turn] = inv[0][turn]turn] = nn[0][turn] = 1; 142 nn[0][turn] = 1; 143 //invn[1][turn] = inv[1][turn]turn] = nn[1][turn] = 1; 144 for(int i = 1; i < mod[turn]; i++) { 145 nn[i][turn] = nn[i - 1][turn] * i % mod[turn]; 146 //inv[i][turn] = inv[mod[turn] % i] * (mod[turn] - mod[turn] / i) % mod[turn]; 147 //invn[i][turn] = invn[i - 1][turn] * inv[i][turn] % mod[turn]; 148 } 149 } 150 return; 151 } 152 153 int main() { 154 155 freopen("cliquers.in", "r", stdin); 156 freopen("cliquers.out", "w", stdout); 157 158 prework(); 159 160 int T; 161 scanf("%d", &T); 162 while(T--) { 163 work(); 164 } 165 return 0; 166 }
两种CRT都写了。
