

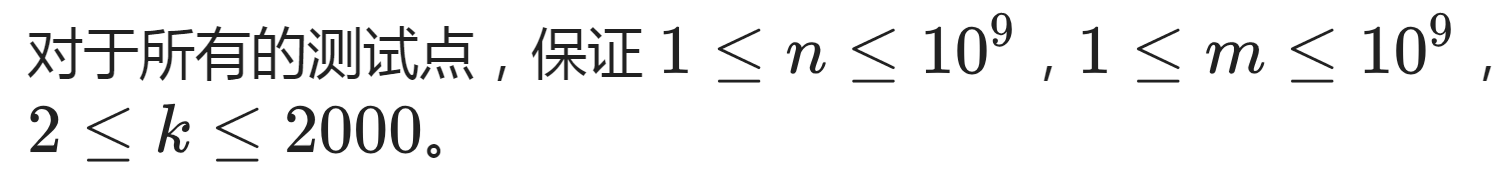
解:首先看这个纯循环到底是什么玩意.....
经过一番打表,发现纯循环小数就是分母与进制互质的既约分数。

1 #include <bits/stdc++.h> 2 3 std::bitset<1001> vis; 4 5 inline bool check(int x, int y) { /// x / y 6 //printf("x = %d y = %d ", x, y); 7 vis.reset(); 8 int rest = x % y; 9 if(!rest) return true; 10 int op = rest; 11 vis[op] = 1; 12 //printf("op = %d ", op); 13 while(true) { 14 rest *= 10; 15 int r = rest % y; 16 //printf("r = %d ", r); 17 if(vis[r]) { 18 //printf("return %d = %d ", r, op); 19 return r == op; 20 } 21 vis[r] = 1; 22 rest = r; 23 } 24 return false; 25 } 26 27 int gcd(int a, int b) { 28 if(!b) return a; 29 return gcd(b, a % b); 30 } 31 32 int main() { 33 34 int n; 35 scanf("%d", &n); 36 37 for(int i = 0; i <= n; i++) { 38 for(int j = 1; j <= n; j++) { 39 if(gcd(i, j) == 1) printf("%d ", (int)check(i, j)); 40 else printf(" "); 41 } 42 puts(""); 43 } 44 45 return 0; 46 }
那么就有了一个很显然的O(nmlogV)的做法...直接暴力枚举然后检验。实测24分。

1 #include <bits/stdc++.h> 2 3 int gcd(int a, int b) { 4 if(!b) return a; 5 return gcd(b, a % b); 6 } 7 8 int main() { 9 int n, m, k, ans = 0; 10 scanf("%d%d%d", &n, &m, &k); 11 if(1ll * n * m > 1000000000) return 0; 12 for(int i = 1; i <= m; i++) { 13 if(gcd(k, i) > 1) continue; 14 for(int j = 1; j <= n; j++) { 15 ans += gcd(i, j) == 1; 16 } 17 } 18 printf("%d ", ans); 19 return 0; 20 }
然后发现最里面那句话有点像phi...仔细思考之后发现不是。
现在开始鬼畜时间...推柿子。
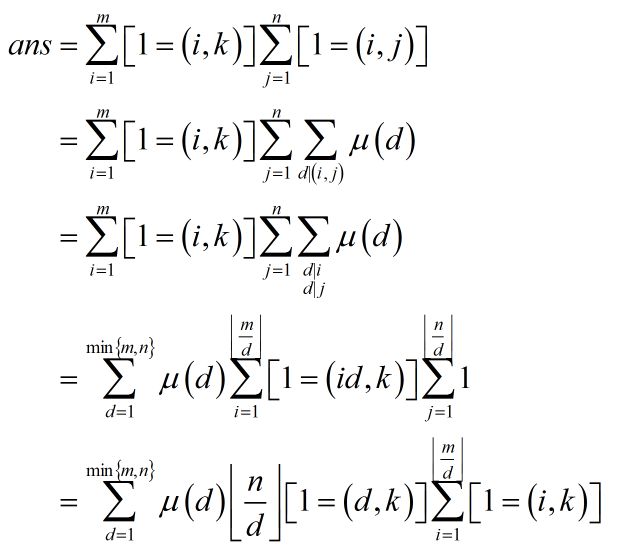
其中有两步转化,分别是把[x=1]用∑μ代替和把[1=(id,k)]用[1=(i,k)][1=(d,k)]代替。
于是考虑最后这个式子,发现有个东西[1=(a,k)],于是设这个东西为g(x),它的前缀和为f(x)。又令F为μ·g的前缀和。
那么答案就是下式:
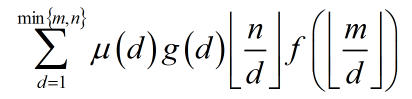
这个东西显然可以分块一波。后两项可以O(1)算,前面的可以线性预处理。于是我们有个O(n)的算法。可以获得84分。

1 #include <bits/stdc++.h> 2 3 typedef long long LL; 4 const int N = 20000010; 5 6 int miu[N], p[N], top, f[N], phi[N], n, m, k, F[N]; 7 bool vis[N]; 8 9 inline void getp(int n) { 10 phi[1] = miu[1] = 1; 11 for(int i = 2; i <= n; i++) { 12 if(!vis[i]) { 13 p[++top] = i; 14 miu[i] = -1; 15 phi[i] = i - 1; 16 } 17 for(int j = 1; j <= top && i * p[j] <= n; j++) { 18 vis[i * p[j]] = 1; 19 if(i % p[j] == 0) { 20 //miu[i * p[j]] = 0; 21 phi[i * p[j]] = phi[i] * p[j]; 22 break; 23 } 24 phi[i * p[j]] = phi[i] * (p[j] - 1); 25 miu[i * p[j]] = -miu[i]; 26 } 27 } 28 return; 29 } 30 31 int gcd(int a, int b) { 32 if(!b) return a; 33 return gcd(b, a % b); 34 } 35 36 inline void prework() { 37 for(int i = 1; i <= k; i++) { 38 f[i] = f[i - 1] + (gcd(i, k) == 1); 39 F[i] = F[i - 1] + (f[i] - f[i - 1]) * miu[i]; 40 } 41 int len = std::min(n, m); 42 for(int i = k + 1; i <= len; i++) { 43 f[i] = f[k] * (i / k) + f[i % k]; 44 F[i] = F[i - 1] + (f[i] - f[i - 1]) * miu[i]; 45 } 46 return; 47 } 48 49 inline int getf(int x) { 50 if(x <= k) return f[x]; 51 return f[k] * (x / k) + f[x % k]; 52 } 53 54 int main() { 55 LL ans = 0; 56 scanf("%d%d%d", &n, &m, &k); 57 if(1ll * n * m < 1e9) { 58 for(int i = 1; i <= m; i++) { 59 if(gcd(k, i) > 1) continue; 60 for(int j = 1; j <= n; j++) { 61 ans += gcd(i, j) == 1; 62 } 63 } 64 printf("%lld ", ans); 65 return 0; 66 } 67 if(n < N) { 68 getp(n); 69 prework(); 70 int len = std::min(n, m); 71 for(int i = 1, j; i <= len; i = j + 1) { 72 j = std::min(n / (n / i), m / (m / i)); 73 /// [i, j] 74 ans += 1ll * (F[j] - F[i - 1]) * (n / i) * getf(m / i); 75 } 76 printf("%lld ", ans); 77 } 78 return 0; 79 }
接下来补个k = 2 / 3的部分分。严格来说应该能应付k是质数的情况,然而后面k都是合数....
推倒过程几乎跟上面一样,最后得到这个东西:
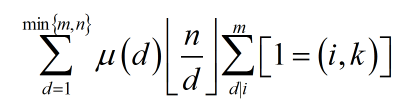
考虑怎么计算后面那个求和符号。当d和k不互质(d是k的倍数)的时候,答案显然是0。否则令t = i / d,答案就是与k互质的t个个数。这个东西我们可以用maxt - maxt / k来O(1)计算。

1 #include <bits/stdc++.h> 2 3 typedef long long LL; 4 const int N = 20000010; 5 6 int miu[N], p[N], top, f[N], phi[N], n, m, k, F[N]; 7 bool vis[N]; 8 9 inline void getp(int n) { 10 phi[1] = miu[1] = 1; 11 for(int i = 2; i <= n; i++) { 12 if(!vis[i]) { 13 p[++top] = i; 14 miu[i] = -1; 15 phi[i] = i - 1; 16 } 17 for(int j = 1; j <= top && i * p[j] <= n; j++) { 18 vis[i * p[j]] = 1; 19 if(i % p[j] == 0) { 20 //miu[i * p[j]] = 0; 21 phi[i * p[j]] = phi[i] * p[j]; 22 break; 23 } 24 phi[i * p[j]] = phi[i] * (p[j] - 1); 25 miu[i * p[j]] = -miu[i]; 26 } 27 } 28 return; 29 } 30 31 int gcd(int a, int b) { 32 if(!b) return a; 33 return gcd(b, a % b); 34 } 35 36 inline int calc(int d) { 37 if((d % k) == 0) { 38 return 0; 39 } 40 d = m / d; 41 return d - d / k; 42 } 43 44 inline void prework() { 45 for(int i = 1; i <= k; i++) { 46 f[i] = f[i - 1] + (gcd(i, k) == 1); 47 F[i] = F[i - 1] + (f[i] - f[i - 1]) * miu[i]; 48 } 49 int len = std::min(n, m); 50 for(int i = k + 1; i <= len; i++) { 51 f[i] = f[k] * (i / k) + f[i % k]; 52 F[i] = F[i - 1] + (f[i] - f[i - 1]) * miu[i]; 53 } 54 return; 55 } 56 57 inline int getf(int x) { 58 if(x <= k) return f[x]; 59 return f[k] * (x / k) + f[x % k]; 60 } 61 62 int main() { 63 LL ans = 0; 64 scanf("%d%d%d", &n, &m, &k); 65 if(1ll * n * m < 1e9) { 66 for(int i = 1; i <= m; i++) { 67 if(gcd(k, i) > 1) continue; 68 for(int j = 1; j <= n; j++) { 69 ans += gcd(i, j) == 1; 70 } 71 } 72 printf("%lld ", ans); 73 return 0; 74 } 75 if((k == 2 || k == 3) && (n <= 10000)) { 76 getp(n); 77 int len = std::min(n, m); 78 for(int i = 1; i <= len; i++) { 79 ans += 1ll * miu[i] * (n / i) * calc(i); 80 } 81 printf("%lld ", ans); 82 return 0; 83 } 84 /*if(n < N) { 85 getp(n); 86 prework(); 87 int len = std::min(n, m); 88 for(int i = 1, j; i <= len; i = j + 1) { 89 j = std::min(n / (n / i), m / (m / i)); 90 /// [i, j] 91 ans += 1ll * (F[j] - F[i - 1]) * (n / i) * getf(m / i); 92 } 93 printf("%lld ", ans); 94 }*/ 95 return 0; 96 }
