洛谷P3299 保护出题人

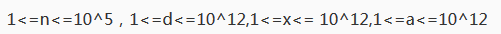
注意每一关的时候，前一关的植物会消失。保留整数指四舍五入。

解：冷静分析一波，列一个式子出来，发现每一关的植物攻击力要是(a_i + ... + a_j) / (x_i + d * (i - j))的最大值。1 <= j <= i

然后把这个东西写成前缀和，分母的i和j分离：(s_i - s_j-1) / (x_i + d * i - d * j))

发现就是两个点(x_i + d * i, s_i)和(d * j, s_j-1)之间的斜率。

于是维护一个下凸包然后凸包上三分就行了。注意到插入的点的横坐标单增，单调栈即可。

整数三分，就考虑l + 1 = r的时候怎么取，也比较好写。

#include <bits/stdc++.h>

typedef long long LL;
const int N = 100010;
const double eps = 1e-12;

struct Vec {
    double x, y;
    Vec(double X = 0, double Y = 0) {
        x = X;
        y = Y;
    }
    inline Vec operator + (const Vec &w) const {
        return Vec(x + w.x, y + w.y);
    }
    inline Vec operator - (const Vec &w) const {
        return Vec(x - w.x, y - w.y);
    }
    inline double operator * (const Vec &w) const {
        return x * w.y - y * w.x;
    }
};
typedef Vec Poi;

Poi node[N];
LL a[N], x[N], sum[N], d;
int n, top, stk[N];

int main() {
    scanf("%d%lld", &n, &d);
    for(int i = 1; i <= n; i++) {
        scanf("%lld%lld", &a[i], &x[i]);
        sum[i] = sum[i - 1] + a[i];
    }
    double ans = 0;
    for(int i = 1; i <= n; i++) {
        Poi now(x[i] + i * d, sum[i]);
        node[i] = Poi(i * d, sum[i - 1]);
        while(top > 1 && (node[stk[top]] - node[stk[top - 1]]) * (node[i] - node[stk[top]]) < eps) {
            top--;
        }
        stk[++top] = i;
        //printf("stk %d = %d (%lld %lld) 
", top, i, i * d, sum[i - 1]);
        //printf("now (%lld %lld) 
", x[i] + i * d, sum[i]);
        int l = 1, r = top;
        while(l < r) {
            int mid = (l + r) >> 1;
            int ml = stk[mid], mr = stk[mid + 1];
            double vl = (double)(sum[i] - sum[ml - 1]) / (x[i] + (i - ml) * d),
                   vr = (double)(sum[i] - sum[mr - 1]) / (x[i] + d * (i - mr));
            //printf("vl = %lf vr = %lf 
", vl, vr);
            //printf("x = %lld y = %lld = %lld + %d * %lld 
", sum[i], x[i] + i * d, x[i], i, d);
            if(vl < vr) {
                l = mid + 1;
            }
            else {
                r = mid;
            }
        }
        ans += (double)(sum[i] - sum[stk[r] - 1]) / (x[i] + (i - stk[r]) * d);
        //printf("ans += %lf 
", (double)(sum[i] - sum[stk[r] - 1]) / (x[i] + (i - stk[r]) * d));
        //printf("r = %d 
", r);
        /*for(int j = 1; j <= top; j++) {
            printf("%d ", stk[j]);
        }
        puts("");*/
    }

    printf("%.0f
", ans);
    return 0;
}