20172315 2018-2019-2 《程序设计与数据结构》第七周学习总结
教材学习内容总结
- 二又查找树是一种含有附加属性的二又树,即其左孩子小于父结点,而父结点又小于或等于右孩子。
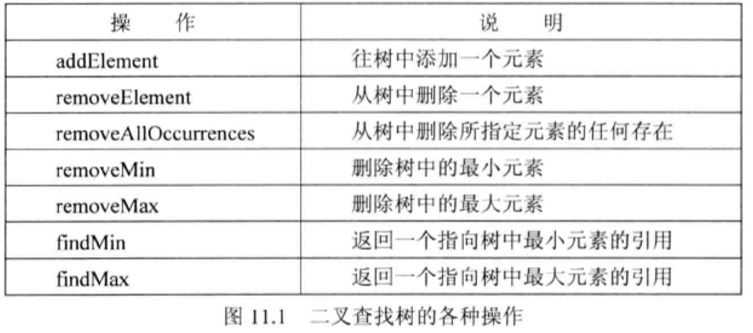
- 每个BinaryTreeNode对象要维护一个指向结点所存储元素的引用,另外还要维护指向结点的每个孩子的引用。
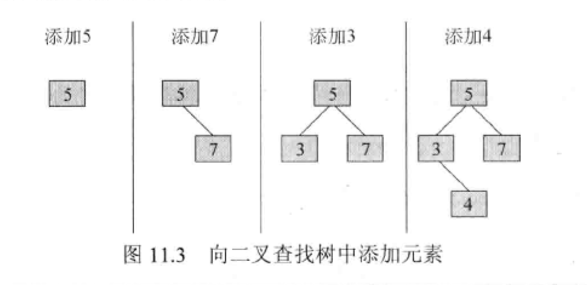
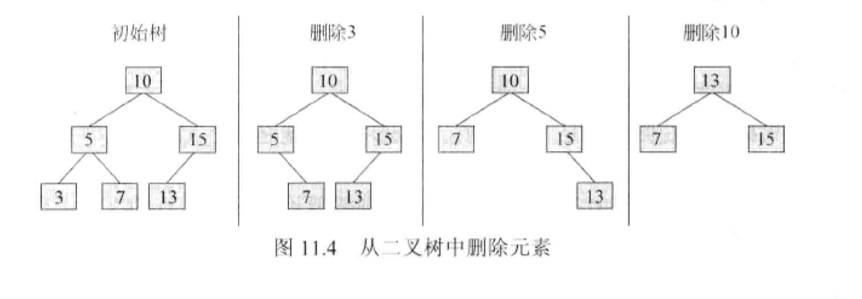
- 从二又查找树中删除一个元素时,必须推选出另一个结点来代替要被删除的那个结点。
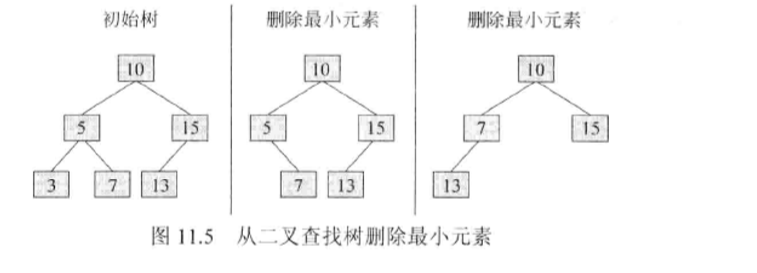
- 二又查找树的最右侧结点会存放最大元素,而其最左侧结点会存放最小元素。
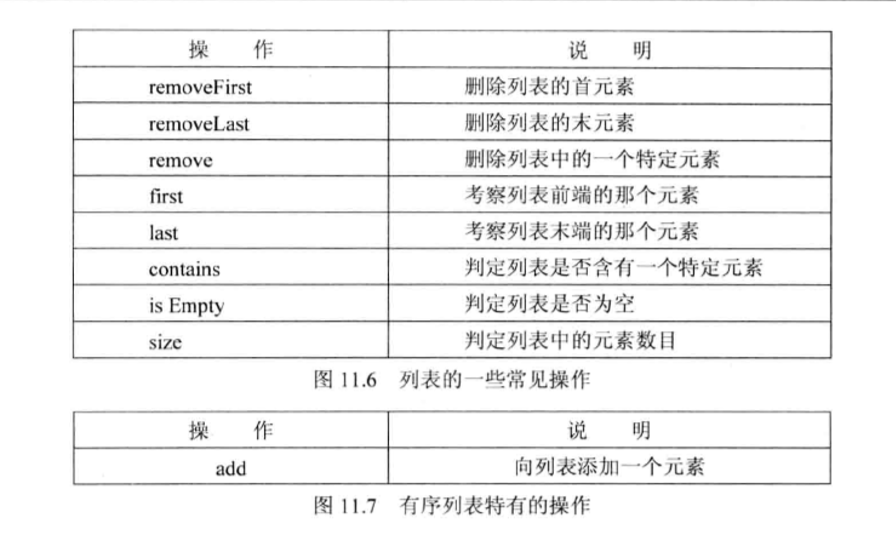
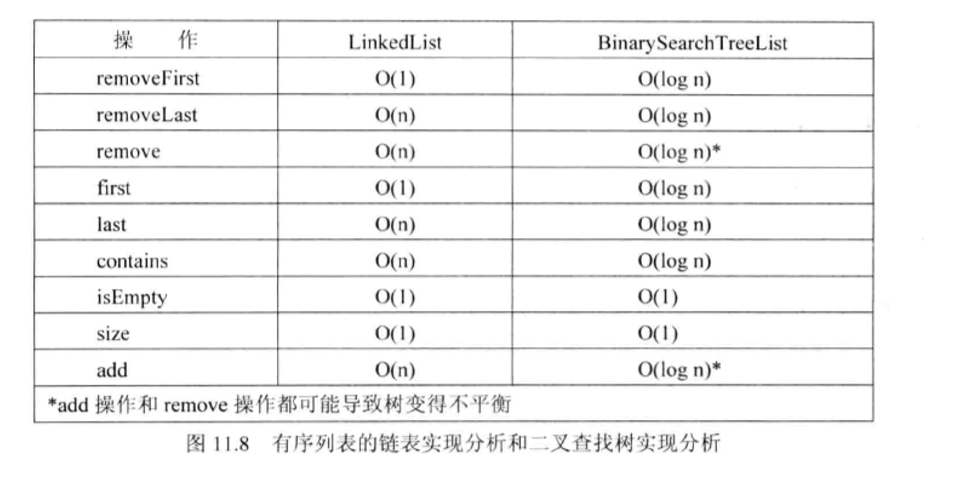
- 如果二又查找树不平衡,其效率可能比线性结构的还要低。
- 右子树的高度减去左子树的高度称为该结点的平衡因子。
- 树(或树的任何子树)只有两种途径能变得不平衡:插入结点或删除结点。
- 红黑树
根结点为黑色。
红色结点的所有孩子都为黑色。
从树根到树叶的每条路径都包含同样数目的黑色结点。
教材学习中的问题和解决过程
- 问题1:书上讲的红黑树不太理解
- 问题1解决方案:在蓝墨云上找到老师推荐的网站加深理解
红黑树(Red-Black Tree,简称R-B Tree),它一种特殊的二叉查找树。
红黑树是特殊的二叉查找树,意味着它满足二叉查找树的特征:任意一个节点所包含的键值,大于等于左孩子的键值,小于等于右孩子的键值。
除了具备该特性之外,红黑树还包括许多额外的信息。
红黑树的每个节点上都有存储位表示节点的颜色,颜色是红(Red)或黑(Black)。
红黑树的特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
关于它的特性,需要注意的是:
第一,特性(3)中的叶子节点,是只为空(NIL或null)的节点。
第二,特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
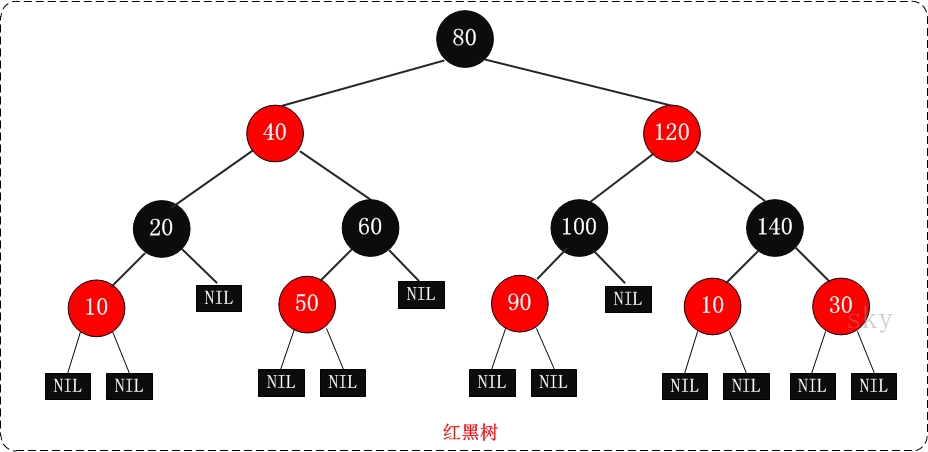
红黑树示意图如下:
- 问题2:书上的avl树无法理解
- 问题2解决方案:在网上查询资料:平衡二叉树定义(AVL):它或者是一颗空树,或者具有以下性质的二叉树:它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
平衡因子(bf):结点的左子树的深度减去右子树的深度
资料
代码调试中的问题和解决过程
- 问题1:对于pp11.8如何实现avl树仍然有疑惑
- 问题1解决方案:在网上找到了一篇博客,参考他的讲解后完成
AVL树(三)之 Java的实现
代码托管
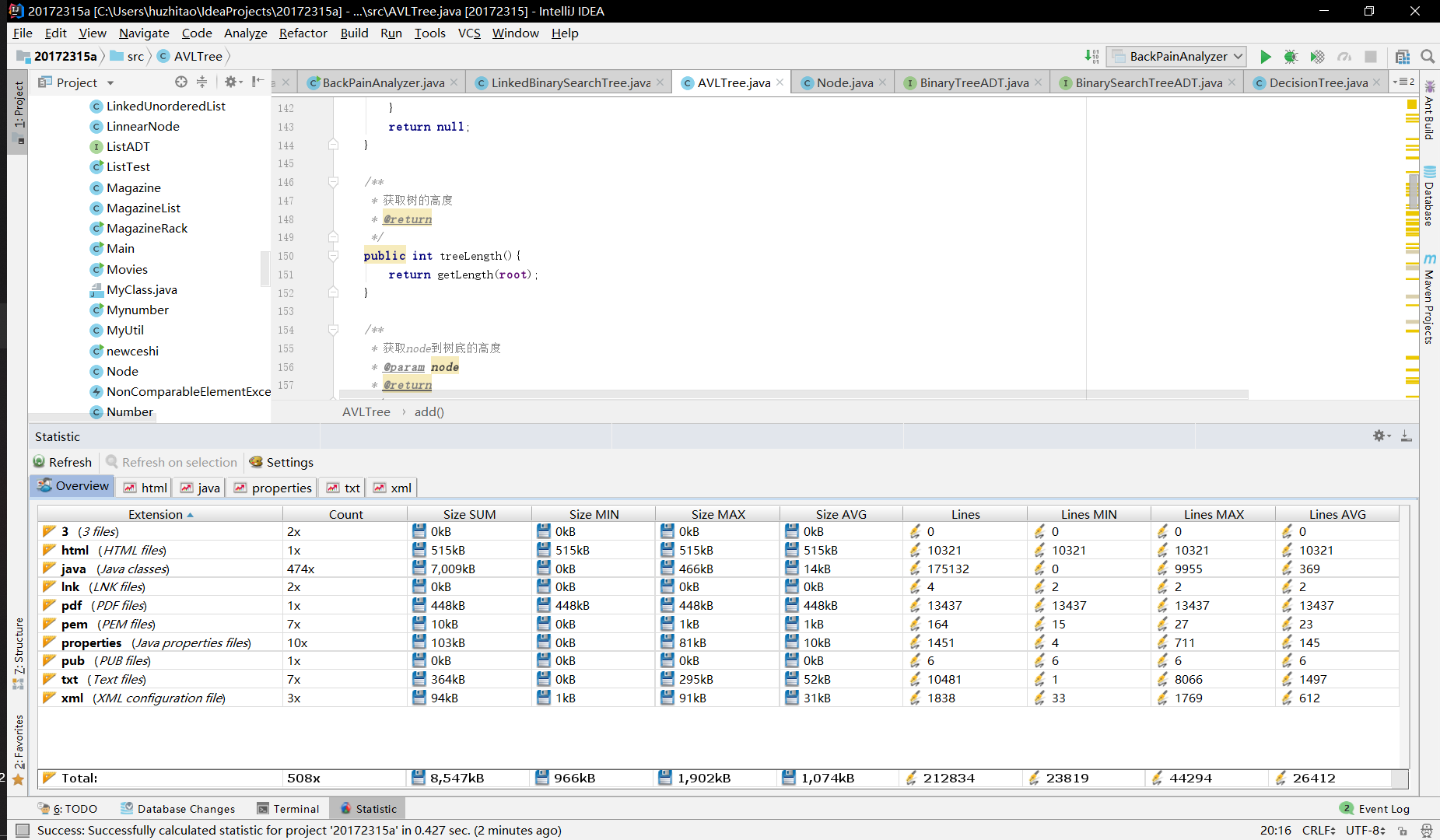
(statistics.sh脚本的运行结果截图)
上周考试错题总结
上周无错题~
结对及互评
点评模板:
- 博客中值得学习的或问题:
- 博客中图片过少
- 对于教材内容解析很到位
- 代码中值得学习的或问题:
- 代码简洁明了
- 代码不太规范,注释过少
点评过的同学博客和代码
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 0/0 | 0/0 | |
| 第二周 | 800/800 | 2/2 | 18/18 | |
| 第三周 | 600/1400 | 3/5 | 22/40 | |
| 第四周 | 700/1300 | 3/8 | 22/62 | |
| 第五周 | 400/1700 | 3/11 | 22/84 | |
| 第六周 | 200/1900 | 2/13 | 20/94 | |
| 第七周 | 400/2300 | 2/15 | 20/114 |