机器学习之决策树（二）

一、复习信息熵

　　为了解决特征选择问题，找出最优特征，先要介绍一些信息论里面的概念。 

　　1、熵（entropy）

　　　　

　　　　python3代码实现：

def calcShannonEnt(dataSet):
    '''
    计算香农熵
    :param dataSet:数据集
    :return: 计算结果
    '''
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet: # 遍历每个实例，统计标签的频数
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): 
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        shannonEnt -= prob * log(prob,2) # 以2为底的对数
    return shannonEnt

　　2、条件熵（conditional entropy）

　　　　

　　　　python3代码实现：

def splitDataSet(dataSet, axis, value):
    '''
    按照给定特征划分数据集
    :param dataSet:待划分的数据集
    :param axis:划分数据集的特征
    :param value: 需要返回的特征的值
    :return: 划分结果列表
    '''
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #chop out axis used for splitting
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

def calcConditionalEntropy(dataSet, i, featList, uniqueVals):
    '''
    计算X_i给定的条件下，Y的条件熵
    :param dataSet:数据集
    :param i:维度i
    :param featList: 数据集特征列表
    :param uniqueVals: 数据集特征集合
    :return: 条件熵
    '''
    conditionEnt = 0.0
    for value in uniqueVals:
        subDataSet = splitDataSet(dataSet, i, value)
        prob = len(subDataSet) / float(len(dataSet))  # 极大似然估计概率
        conditionEnt += prob * calcShannonEnt(subDataSet)  # 条件熵的计算
    return conditionEnt

　　3、信息增益（information gain） 

　　　　

　　　　python3代码实现：

def calcInformationGain(dataSet, baseEntropy, i):
    '''
    计算信息增益
    :param dataSet:数据集
    :param baseEntropy:数据集的信息熵
    :param i: 特征维度i
    :return: 特征i对数据集的信息增益g(D|X_i)
    '''
    featList = [example[i] for example in dataSet]  # 第i维特征列表
    uniqueVals = set(featList)  # 转换成集合
    newEntropy = calcConditionalEntropy(dataSet, i, featList, uniqueVals)
    infoGain = baseEntropy - newEntropy  # 信息增益，就yes熵的减少，也就yes不确定性的减少
    return infoGain

　　看一个简单的例子：

　　随机事件未按照某个属划的不同取值划分时的熵减去按照某个属性的不同取值划分时的平均熵。即前后两次熵的差值。

　　还是对于打垒球的例子，未按照某个属划的不同取值划分时的熵即H(活动)已算出未0.94。现在按照天气属性的不同取值来划分，发现天气属性有3个不同取值分别为晴，阴，雨。

　　划分好后如下图所示。

天气	温度	湿度	风速	活动
晴	炎热	高	弱	取消
晴	炎热	高	强	取消
晴	适中	高	弱	取消
晴	寒冷	正常	弱	进行
晴	适中	正常	强	进行
阴	炎热	高	弱	进行
阴	寒冷	正常	强	进行
阴	适中	高	强	进行
阴	炎热	正常	弱	进行
雨	寒冷	正常	强	取消
雨	适中	高	强	取消
雨	适中	高	弱	进行
雨	寒冷	正常	弱	进行
雨	适中	正常	弱	进行

　　在天气为晴时有5种情况，发现活动取消有3种，进行有2种，计算现在的条件熵

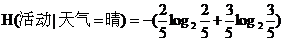　　=0.971

　　同理天气为阴时有4种情况，活动进行的有4种，则条件熵为：

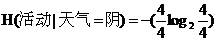　　=0

　　同理天气为雨时有5种情况，活动取消的有2种，进行的有3种，则条件熵为：

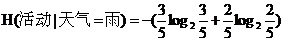　　=0.971

　　由于按照天气属性不同取值划分时，天气为晴占整个情况的5/14，天气为阴占整个情况的4/14，天气为雨占整个情况的5/14，则按照天气属性不同取值划分时的带权平均值熵为：

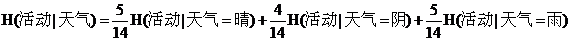　　　　算出的结果约为0.693.　　　　

　　则此时的信息增益Gain（活动，天气）= H(活动) - H(活动|天气) = 0.94- 0.693 = 0.246

　　同理我们可以计算出按照温度属性不同取值划分后的信息增益：

　　Gain（活动，温度）= H(活动) - H(活动|温度) = 0.94- 0.911 = 0.029

　　按照湿度属性不同取值划分后的信息增益：

　　Gain（活动，湿度）= H(活动) - H(活动|湿度) = 0.94- 0.789 = 0.151

　　按照风速属性不同取值划分后的信息增益：

　　Gain（活动，风速）= H(活动) - H(活动|风速) = 0.94- 0.892 = 0.048

　　对于信息增益的理解

　　信息增益就是两个熵的差，当差值越大说明按照此划分对于事件的混乱程度减少越有帮助。

　　计算各个属性的信息增益，并选择信息增益最大的属性的代码如下

#定义按照某个特征进行划分的函数splitDataSet
#输入三个变量（待划分的数据集，特征，分类值）
#axis特征值中0代表no surfacing，1代表flippers
#value分类值中0代表否，1代表是
def splitDataSet(dataSet,axis,value):
    retDataSet = []
    for featVec in dataSet:#取大列表中的每个小列表
        if featVec[axis]==value:
            reduceFeatVec=featVec[:axis]
            reduceFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reduceFeatVec)
    
    return retDataSet #返回不含划分特征的子集
    
def chooseBestFeatureToSplit(dataSet):
    numFeature = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInforGain = 0
    bestFeature = -1
    
    for i in range(numFeature):
        featList = [number[i] for number in dataSet]#得到某个特征下所有值（某列）
        uniquelVals = set(featList) #set无重复的属性特征值，得到所有无重复的属性取值
        
        #计算每个属性i的概论熵
        newEntropy = 0
        for value in uniquelVals:
            subDataSet = splitDataSet(dataSet,i,value)#得到i属性下取i属性为value时的集合
            prob = len(subDataSet)/float(len(dataSet))#每个属性取值为value时所占比重
            newEntropy+= prob*calcShannonEnt(subDataSet)
        inforGain = baseEntropy - newEntropy #当前属性i的信息增益
        
        if inforGain>bestInforGain:
            bestInforGain = inforGain
            bestFeature = i
   
return bestFeature#返回最大信息增益属性下标

　　　相对应地，以信息增益作为划分训练数据集的特征的算法称为ID3算法　

　　4、信息增益比（information gain ratio） 

　　　　

　　　　python3代码实现：

　　　　

def calcInformationGainRatio(dataSet, baseEntropy, i):
    '''
    计算信息增益比
    :param dataSet:数据集
    :param baseEntropy:数据集的信息熵
    :param i: 特征维度i
    :return: 特征i对数据集的信息增益比gR(D|X_i)
    '''
    return calcInformationGain(dataSet, baseEntropy, i) / baseEntropy

　　相应地，用信息增益比来选择特征的算法称为C4.5算法。

二、决策树定义

　　决策树是一种树型结构，其中每个内部结点 表示在一个属性上的测试，每个分支代表一 个测试输出，每个叶结点代表一种类别。

　　　　 决策树学习是以实例为基础的归纳学习。

　　　　 决策树学习采用的是自顶向下的递归方法， 其基本思想是以信息熵为度量构造一棵熵值 下降最快的树，

　　　　　到叶子节点处的熵值为零， 此时每个叶节点中的实例都属于同一类。

　　上面例子最终形成的决策树如下：

　　

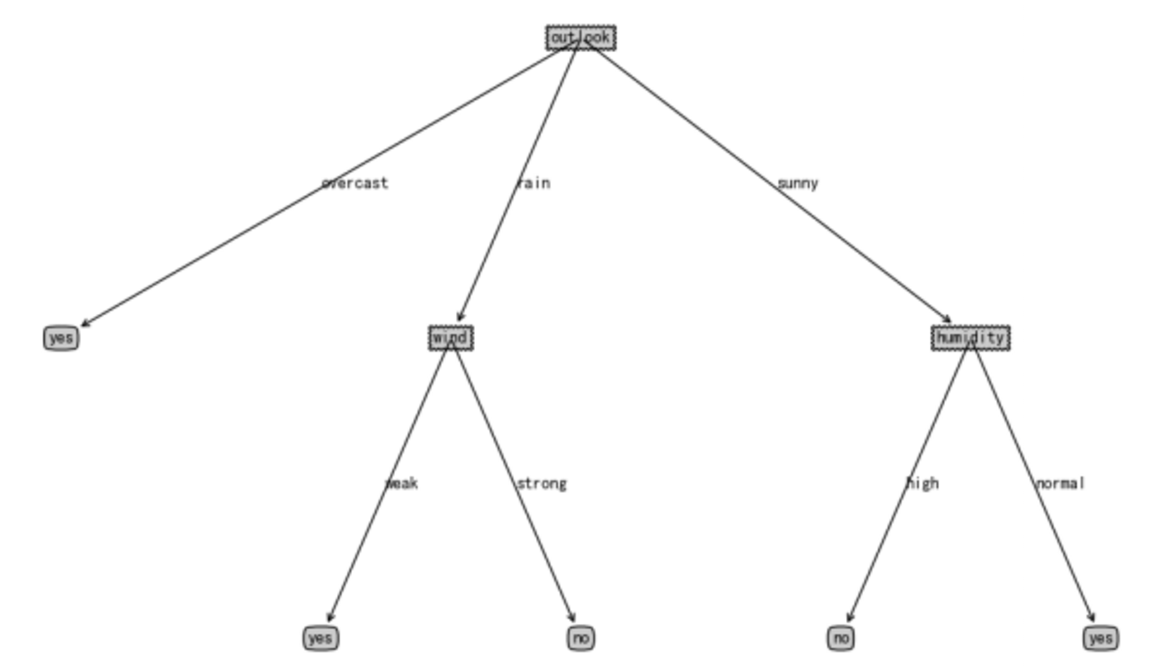
　　整个程序的代码：

from math import log
from operator import *

def storeTree(inputTree,filename):
    import pickle
    fw=open(filename,'wb') #pickle默认方式是二进制，需要制定'wb'
    pickle.dump(inputTree,fw)
    fw.close()
    
def grabTree(filename):
    import pickle
    fr=open(filename,'rb')#需要制定'rb'，以byte形式读取
    return pickle.load(fr)


def createDataSet():
    '''
    dataSet=[[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]
    labels = ['no surfacing','flippers']
    '''
    dataSet = [['sunny','hot','high','weak','no'],
               ['sunny','hot','high','strong','no'],
               ['overcast','hot','high','weak','yes'],
               ['rain','mild','high','weak','yes'],
               ['rain','cool','normal','weak','yes'],
               ['rain','cool','normal','strong','no'],
               ['overcast','cool','normal','strong','yes'],
               ['sunny','mild','high','weak','no'],
               ['sunny','cool','normal','weak','yes'],
               ['rain','mild','normal','weak','yes'],
               ['sunny','mild','normal','strong','yes'],
               ['overcast','mild','high','strong','yes'],
               ['overcast','hot','normal','weak','yes'],
               ['rain','mild','high','strong','no']]
    labels = ['outlook','temperature','humidity','wind']
    return dataSet,labels

def calcShannonEnt(dataSet):#计算香农熵
    numEntries = len(dataSet)
    
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]   #取得最后一列数据，该属性取值情况有多少个
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel]+=1
    
    #计算熵
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2)
        
    return shannonEnt

#定义按照某个特征进行划分的函数splitDataSet
#输入三个变量（待划分的数据集，特征，分类值）
#axis特征值中0代表no surfacing，1代表flippers
#value分类值中0代表否，1代表是
def splitDataSet(dataSet,axis,value):
    retDataSet = []
    for featVec in dataSet:#取大列表中的每个小列表
        if featVec[axis]==value:
            reduceFeatVec=featVec[:axis]
            reduceFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reduceFeatVec)
    
    return retDataSet #返回不含划分特征的子集
    
def chooseBestFeatureToSplit(dataSet):
    numFeature = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInforGain = 0
    bestFeature = -1
    
    for i in range(numFeature):
        featList = [number[i] for number in dataSet]#得到某个特征下所有值（某列）
        uniquelVals = set(featList) #set无重复的属性特征值，得到所有无重复的属性取值
        
        #计算每个属性i的概论熵
        newEntropy = 0
        for value in uniquelVals:
            subDataSet = splitDataSet(dataSet,i,value)#得到i属性下取i属性为value时的集合
            prob = len(subDataSet)/float(len(dataSet))#每个属性取值为value时所占比重
            newEntropy+= prob*calcShannonEnt(subDataSet)
        inforGain = baseEntropy - newEntropy #当前属性i的信息增益
        
        if inforGain>bestInforGain:
            bestInforGain = inforGain
            bestFeature = i
   
    return bestFeature#返回最大信息增益属性下标
    
#递归创建树,用于找出出现次数最多的分类名称
def majorityCnt(classList):
    classCount={}
    for vote in classList:#统计当前划分下每中情况的个数
        if vote not in classCount.keys():
            classCount[vote]=0
        classCount[vote]+=1
    sortedClassCount=sorted(classCount.items,key=operator.itemgetter(1),reversed=True)#reversed=True表示由大到小排序
    #对字典里的元素按照value值由大到小排序
   
    return sortedClassCount[0][0]


def createTree(dataSet,labels):
    classList=[example[-1] for example in dataSet]#创建数组存放所有标签值,取dataSet里最后一列（结果）
    #类别相同，停止划分
    if classList.count(classList[-1])==len(classList):#判断classList里是否全是一类，count() 方法用于统计某个元素在列表中出现的次数
        return classList[-1] #当全是一类时停止分割
    #长度为1，返回出现次数最多的类别
    if len(classList[0])==1: #当没有更多特征时停止分割，即分到最后一个特征也没有把数据完全分开，就返回多数的那个结果
        return majorityCnt(classList)
    #按照信息增益最高选取分类特征属性
    bestFeat=chooseBestFeatureToSplit(dataSet)#返回分类的特征序号,按照最大熵原则进行分类
    bestFeatLable=labels[bestFeat] #该特征的label, #存储分类特征的标签
    
    myTree={bestFeatLable:{}} #构建树的字典
    del(labels[bestFeat]) #从labels的list中删除该label
    
    featValues=[example[bestFeat] for example in dataSet]
    uniqueVals=set(featValues)
    for value in uniqueVals:
        subLables=labels[:] #子集合 ,将labels赋给sublabels，此时的labels已经删掉了用于分类的特征的标签
        #构建数据的子集合，并进行递归
        myTree[bestFeatLable][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLables)
    return myTree


if __name__=="__main__":
    my_Data,labels = createDataSet()
    
    #print(calcShannonEnt(my_Data))
    Mytree = createTree(my_Data,labels)
    print(Mytree)

　　其他决策树例子：下图是建立好的决策树模型，数据的属性有4个：年龄、长相、收入、是否公务员，根据此模型，可以得到最终是见或者不见。 

　　

三、决策树算法

　　主要的算法有：ID3算法 、C4.5算法 、CART算法

　　参考资料：https://blog.csdn.net/HerosOfEarth/article/details/52347820

　　　　　　　https://blog.csdn.net/LY_ysys629/article/details/72809129

　　　　　　　https://www.cnblogs.com/wsine/p/5180321.html

本文参考文档：https://www.cnblogs.com/kanjian2016/p/7746005.html

　　　　　　　https://blog.csdn.net/HerosOfEarth/article/details/52347820