大纲:
二叉树上的宽度搜索
图上的宽度搜索
拓扑排序
棋盘上的宽度搜索
什么时候使用宽度优先搜索呢?
图的遍历
层级遍历
由点及面
拓扑排序
最短路径
仅限简单图求最短路径:即图中每条边长度都是1,并且没有方向。
如果题目问最短路径,那么除了BFS还可能是什么算法呢?如果是问最长路径呢?
答:那么就是动态规划算法。如果是最长路径,那么就可能是DFS和DP。
二叉树上的宽度优先搜索
图的遍历(层级遍历)
这里实现的是树的层级遍历,是结合队列数据结构实现的。在这里并未详细给出将实现宽度优先搜索算法的结果做何处理,这里可以理解为输出,也可以单独声明一个顺序表,然后将在队列头部出队的元素依次加入顺序表中,这样形成的结果就是宽度优先搜索实现得到的结果。
注:树是图的一种特殊形态,树属于图。

在这里简单介绍一下,BFS算法结束的条件

据上图原理介绍,退出while循环的条件是声明的队列为空。
1 class Solution { 2 public: 3 vector<vector<int>> levelOrder(TreeNode* root) { 4 //用于存储结果 5 vector<vector<int>>* result = new vector<vector<int>>(); 6 if(root == nullptr) 7 { 8 return *result; 9 } 10 11 //队列用于实现层级遍历 12 queue<TreeNode*>* que = new queue<TreeNode*>(); 13 que->push(root); 14 15 while(!que->empty()) 16 { 17 //用于存储每层的结点中存储的数值 18 vector<int>* level = new vector<int>(); 19 int size = que->size(); 20 for(int i = 0; i < size; i++) 21 { 22 TreeNode* node = que->front(); 23 que->pop(); 24 level->push_back(node->val); 25 26 if(node->left != nullptr) 27 { 28 que->push(node->left); 29 } 30 if(node->right != nullptr) 31 { 32 que->push(node->right); 33 } 34 } 35 result->push_back(*level); 36 // delete[]; 37 } 38 return *result; 39 } 40 };
上面代码中通过乐扣网测试
上面代码中声明了两个vector容器和一个queue队列
vector容器的result是用来存放层级遍历的最终结果,level是当层级遍历到某一层时用来存储该层的遍历结果,待该层遍历结束时,将此level添加到result中,形成最后的结果。
BFS的步骤
1.创建一个临时队列,把树的起始结点放到队列中
2.while语句判断队列不为空时,处理队列中的结点并拓展出新的结点
3.对队列中的数据元素进行for循环,根据本层的结点拓展出下一层的结点并存储在队列中。
注意:
我们知道队列是一种先进先出的数据容器,我们只能访问队头和队尾的元素而无法访问其他位置的元素,所以在进行for循环时,每一个for循环内应该由如下三步操作
1.访问队头元素并查找队头元素的左右孩子节点
2.将查找到的左右孩子节点在队尾进行入队操作
3.对队头元素执行出队操作,使队头元素称为下一个节点。
关于分层的要点
分层的实现是通过队列的长度来实现的,也就是以二叉树的每一层为一个层级。
注意:使用队列是实现宽度搜索算法的标准数据结构,而栈是深度优先搜索算法的标准数据结构
什么是序列化
将“内存”中结构化得数据编程“字符串”的过程
序列化:object to string
反序列化: string to object
什么时候需要序列化
1.将内存中的数据持久存储时
内存中重要的数据不能只是呆在内存里,这样断电就没有了,所以需要用一种方式写入硬盘,在需要的时候,能否在从硬盘中读出来再内存中重新创建
2.网络传输时
机器与机器之间交换数据的时候,不可能互相去读对方的内存。只能将数据编程字符流数据(字符串)后通过网络传输过去。接收的一方在将字符串解析后存储到内存中。
一些常见的序列化手段
XML
Json
Thrift(by Facebook)
序列化算法
一些序列化的例子
比如一个数组,里面都是整数,我们可以简单的序列化为“[1, 2, 3]”
一个整数链表,我们可以序列化为,“1 -> 2 -> 3”
一个哈希表,我们可以将其序列化为“{"key": "value"}”
序列化算法设计时需要考虑的因素:
压缩率。对于网络传输和磁盘存储而言,当然希望更节省。
如Thrift, ProtoBuf都是为了更快的传输数据和节省存储空间而设计的
可读性。我们希望开发人员,能够以通过序列化后的数据直接看懂原始数据是什么
如Json, LintCode的输入数据
二叉树的序列化
前面介绍的序列化和我们在这里的序列化只是逻辑上相同,而我们并不是要真正实现前面介绍的序列化。而是将前面介绍的序列化的逻辑应用到这里而已。
这里二叉树的序列化就是能够严格按照一定顺序输出二叉树上的各个结点元素,得到输出的一个序列型数组。而反序列化就是要根据这个数组还原二叉树。举例如图所示

你可以使用任何你想要的方法进行序列化,只要保证能够解析回来即可
LintCode采用的BFS的方式对二叉树数据进行序列化,这样的好处是你可以更容易地画出整棵二叉树
题目及解答:
http://www.lintcode.com/en/problem/binary-tree-serialization/
http://www.jiuzhang.com/solutions/binary-tree-serialization/
图上的宽度优先搜索
图上的宽度优先搜索算法与树上的宽度优先搜索算法有什么区别呢?
树上具有确定的上下级关系,是父子关系,是单向的关系,如A是B的双亲结点,而B只能是A的孩子结点。而图上的顶点之间是平等的,之间的关系是则是邻居关系,是双向的,比如A是B的邻居,B是A的邻居。那么这样的平等关系会导致什么样的宽度优先搜索呢?如图所示
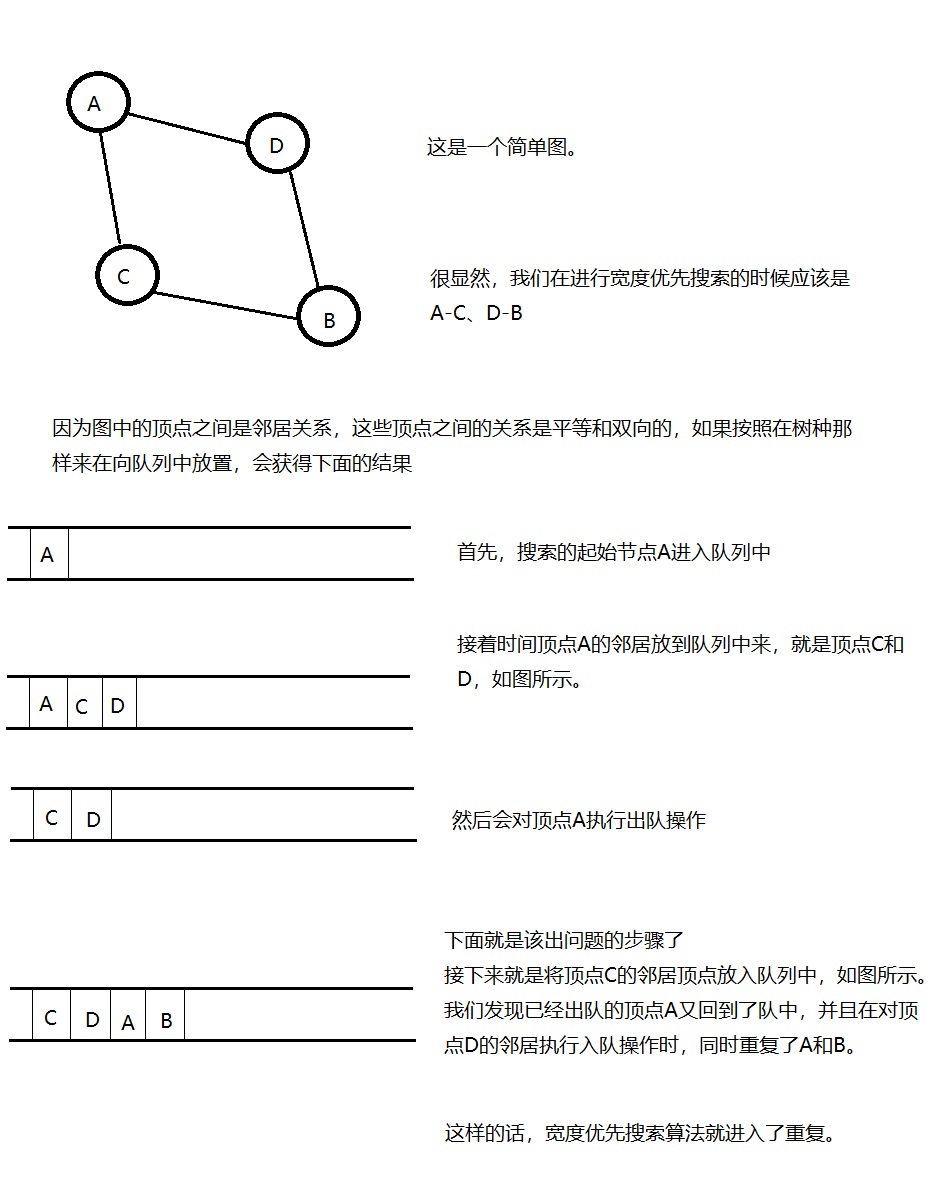
为了解决上图中描述的问题,就需要有一个操作或者记录,来记录某个顶点是否已经进入过了队列,如果进入过了队列,那么这个顶点就应该被标记为进入过队列,在后面的操作中就不再对其进行入队操作。而实现这个记录的操作我们通过HashMap来实现。
这里使用Hash与HashMap是有区别的,如果这里只简单的记录某个顶点是否进入过队列中,就是用Hash,如果除了记录是否进入过队列之外还需要记录其他的信息,则采用HashMap。
图可能会被嵌套在社交网络中来考察。
六度理论:是指地球上所有的人都可以通过六层以内的关系链和其他任何人联系起来,也就是说,你和任何一个陌生人之间所间隔的人不会超过六个。
那么可能会考察一个社交网络中某两个人A和B最少能隔着几个人认识,就是A和B之间的度是多少。那么解决此类问题的标准算法就是宽度优先搜索算法。就是从A开始进行层次遍历,看在第几层的时候找到了B。
图的遍历(由点及面)
这里所说的由点及面问题,用英文来说就是connect compent,就是连通块问题,也就是所说的判断连通性问题,就是通过一个点找到其他所有的与这个点连通的点。这个问题是宽度优先搜索的典型问题,也通常将求解连通块的问题叫做灌水法。
判断一个图是否是树状结构,下面两个条件是充要条件。
条件1:N个顶点刚好有N-1条边 条件2:N个点连通(所有点都是连通的)
那么判断一个图是否是树状结构,就需要分成两个过程来判断
步骤1:判断是否是N个顶点和N-1条边。
步骤2:判断所有点是否连通(方法就是判断能否从顶点0开始沿着边把所有的顶点都找到)
问:如何使用基本数据结构表示一个图?
求连通块的问题的算法问题通常成为灌水法,就是使用BFS去求连通性的算法。
判断连通性问题就是通过一个点开始,看能否把所有的点都找齐,如果都找齐,则说明这些点是连通的,反之,则不连通。
http://www.lintcode.com/problem/graph-valid-tree/
http://www.jiuzhang.com/solutions/graph-valid-tree/
在代码中queue和hash就好比是数据结构中的一对好基友,总是一块出现,通常都是一起操作的。向队列中添加一个数,就也向哈希表中添加一个数。
1 using adjancentGraph = unordered_map<int, unordered_set<int>>; 2 class solution_hash{ 3 public: 4 bool validTree(int n, vector<vector<int>>& edges){ 5 if(n == 0) return false; 6 if(edges.size() != n-1) return false; 7 8 adjancentGraph graph = initializeGraph(n, edges); 9 queue<int> que; 10 unordered_set<int> hash; 11 12 que.push(0); 13 hash.insert(0); 14 15 while(!que.empty()) 16 { 17 //取队首的结点 18 int node = que.front(); 19 que.pop(); 20 //获得队首结点的邻居 21 auto neighbors = graph[node]; 22 23 //看邻居们是否进入过hash_set中 24 //若进入过,则直接下一个邻居 25 //若没进入过,则将这个邻居压入hash_set中,并压入队列中 26 for(unordered_set<int>::iterator it = neighbors.begin(); it != neighbors.end(); it++) 27 { 28 if(hash.find(*it) != neighbors.end()) continue; 29 hash.insert(*it); 30 que.push(*it); 31 } 32 } 33 return (hash.size() == n); 34 35 } 36 37 private: 38 adjancentGraph initializeGraph(int n, vector<vector<int>>& edges){ 39 //建立一张空图 40 adjancentGraph graph; 41 42 //向空图中加入各结点 43 for(int i = 0; i < n; i++) 44 { 45 unordered_set<int> temp; 46 graph.insert(make_pair(i, temp)); 47 } 48 49 //建立各结点之间的连接 50 for(auto edge:edges) 51 { 52 int u = edge[0]; 53 int v = edge[1]; 54 55 graph[u].insert(v); 56 graph[v].insert(u); 57 } 58 return graph; 59 } 60 };
深度拷贝问题
有如下语句
List<Integer> list1 = new ArrayList<>(); List<Integer> list2 = list1;
List<Integer> list3 = new ArrayList<list1>;
显然,list1和list2都是指针变量,指向同一个ArrayList。通过对list1的操作同样会影响list2。
这种拷贝就叫做浅拷贝,只拷贝了引用。
对于list3来讲,是将list1作为拷贝构造函数的参数值传入,这样就在内存中又开辟了一块内存空间,其中存储的内容与list1指向的内存块中存储的数据元素完全相同。但是list1和list3是完全相互独立的两个变量,互不影响。
深拷贝的另外一个名字就是克隆。
http://www.lintcode.com/problem/clone-graph/
http://www.jiuzhang.com/solutions/clone-graph/
注意在实现功能的时候,要善于使用函数,将不同的小功能在不同的子函数体中实现。这样就不至于让代码看起来很混乱,这也算是分治思想体现的一点。
一个好的程序要有很清晰的逻辑结构,第一步做什么,第二步做什么等。
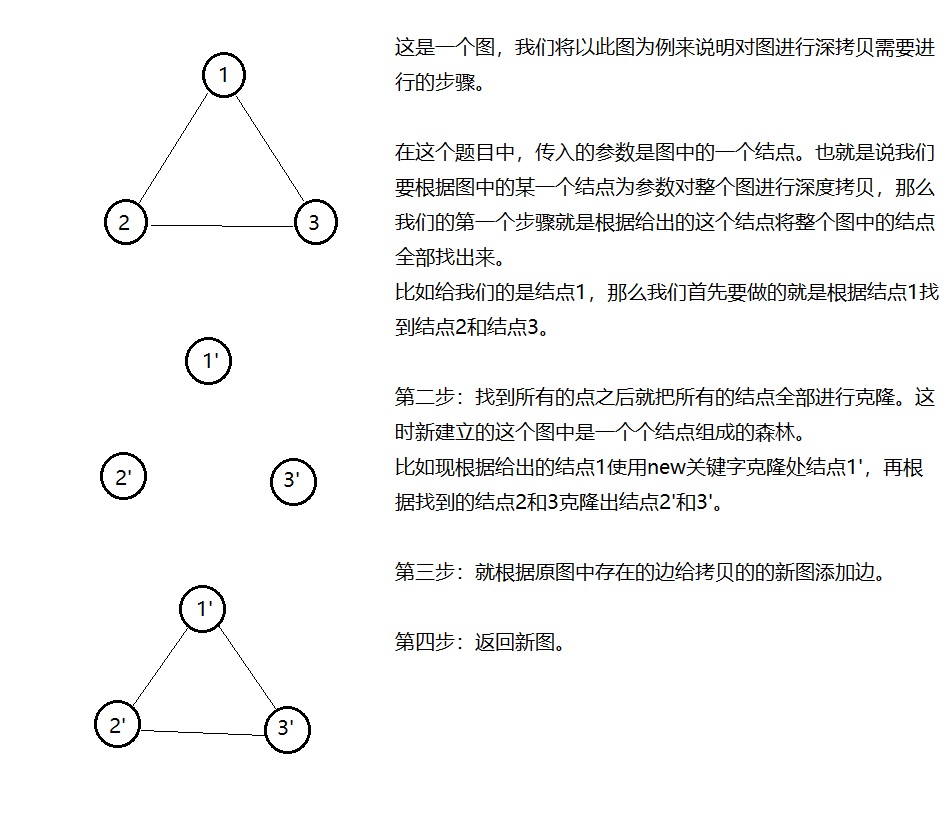
能够使用BFS解决的问题,一定不要用DFS去解决,因为用递归实现的DFS可能造成StackOverflow。
拓扑排序
拓扑排序是排序算法吗?
拓扑排序不是排序算法。百度百科中的解释如下:

拓扑排序就是使用BFS来实现,这样简单易懂。
在拓扑排序中就使用入度来统计。
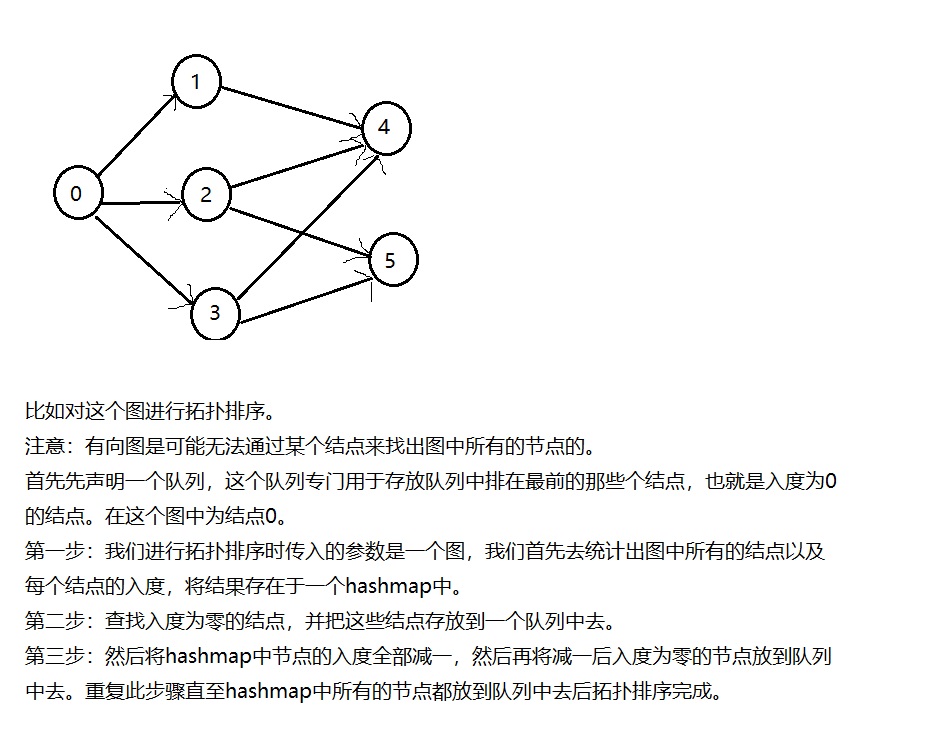
有的题目会问某个图能否进行拓扑排序,那么解法也是首先按照上述方法进行拓扑排序,最后用一个判断来判断出能否进行拓扑排序,判断条件就是看拓扑排序完成后队列中的节点数量是否与原图中节点数量相等,若相等,则说明可以进行拓扑排序,若不相等,则不能进行拓扑排序。
若让找出所有的拓扑排序就只能使用DFS。
矩阵中的宽度优先搜索
图
N个点,M条边
M最大是O(N^2)的级别
图上BFS时间复杂度 = O(N+M),但是说是O(M)问题也不大,因为M一般比N大
所以最坏情况可能是O(N^2)
矩阵
R行C列
R*C个点, R*C*2条边(每个点上下左右四条边,没条边被2个点共享)
矩阵中BFS时间复杂度 = O(R*C)