ython计算KL散度
import numpy as np
import scipy.stats
x = [np.random.randint(1,11) for i in range(10)]
print(x)
print(np.sum(x))
px = x/np.sum(x)#归一化
print(px)
y = [np.random.randint(1, 11) for i in range(10)]
print(y)
print(np.sum(y))
py = y / np.sum(y)#归一化
print(py)
## scipy计算函数可以处理非归一化情况,因此这里使用# scipy.stats.entropy(x, y)或scipy.stats.entropy(px, py)均可
KL = scipy.stats.entropy(x, y)
print(KL)
#自己编程实现
kl= 0.0
for i in range(10):
kl += px[i] * np.log(px[i]/py[i])
print(kl)
#TensorFlow的神经网络
import sys;
sys.path.append("/home/hxj/anaconda3/lib/python3.6/site-packages")
import tensorflow as tf
import numpy as np
x_data = np.random.rand(100).astype(np.float32)
y_data = x_data*0.1+0.3
print(x_data)
print(y_data)
Weights = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
biases = tf.Variable(tf.zeros([1]))
y = Weights*x_data + biases
print(y)
loss = tf.reduce_mean(tf.square(y-y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for step in range(201):
sess.run(train)
if step % 20 == 0:
print(step, sess.run(Weights), sess.run(biases))
#Python画2D图
from functools import partial
import numpy
from matplotlib import pyplot
# Define a PDF
x_samples = numpy.arange(-3, 3.01, 0.01)
PDF = numpy.empty(x_samples.shape)
PDF[x_samples < 0] = numpy.round(x_samples[x_samples < 0] + 3.5) / 3
PDF[x_samples >= 0] = 0.5 * numpy.cos(numpy.pi * x_samples[x_samples >= 0]) + 0.5
PDF /= numpy.sum(PDF)
# Calculate approximated CDF
CDF = numpy.empty(PDF.shape)
cumulated = 0
for i in range(CDF.shape[0]):
cumulated += PDF[i]
CDF[i] = cumulated
# Generate samples
generate = partial(numpy.interp, xp=CDF, fp=x_samples)
u_rv = numpy.random.random(10000)
x = generate(u_rv)
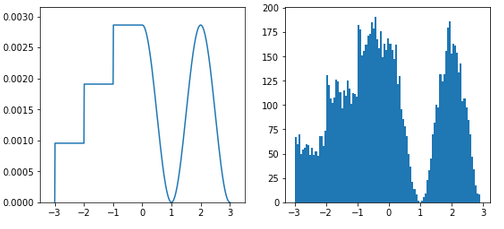
# Visualization
fig, (ax0, ax1) = pyplot.subplots(ncols=2, figsize=(9, 4))
ax0.plot(x_samples, PDF)
ax0.axis([-3.5, 3.5, 0, numpy.max(PDF)*1.1])
ax1.hist(x, 100)
pyplot.show()
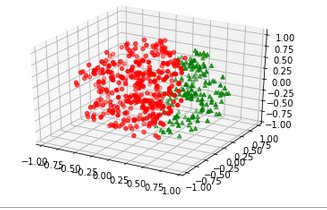
#Python画3D图
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
# 采样个数500
n_samples = 500
dim = 3
# 先生成一组3维正态分布数据,数据方向完全随机
samples = np.random.multivariate_normal(
np.zeros(dim),
np.eye(dim),
n_samples
)
# 通过把每个样本到原点距离和均匀分布吻合得到球体内均匀分布的样本
for i in range(samples.shape[0]):
r = np.power(np.random.random(), 1.0/3.0)
samples[i] *= r / np.linalg.norm(samples[i])
upper_samples = []
lower_samples = []
for x, y, z in samples:
# 3x+2y-z=1作为判别平面
if z > 3*x + 2*y - 1:
upper_samples.append((x, y, z))
else:
lower_samples.append((x, y, z))
fig = plt.figure('3D scatter plot')
ax = fig.add_subplot(111, projection='3d')
uppers = np.array(upper_samples)
lowers = np.array(lower_samples)
# 用不同颜色不同形状的图标表示平面上下的样本
# 判别平面上半部分为红色圆点,下半部分为绿色三角
ax.scatter(uppers[:, 0], uppers[:, 1], uppers[:, 2], c='r', marker='o')
ax.scatter(lowers[:, 0], lowers[:, 1], lowers[:, 2], c='g', marker='^')
plt.show()